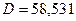Среднее арифметическое выборки

К У Р С О В А Я Р А Б О Т А

	Математические методы в бурении

По дисциплине __________________________

________

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Использование современной компьютерной техники и программного обеспечения для решения прикладной задачи из инженерно-буровой практики

Тема:

________

________

________

Выполнил: студент гр. РТ-10 ______________ / Рыжиков С.В./

^{(подпись) (Ф.И.О.)}

ОЦЕНКА: _____________

ДАТА: ___________________

ПРОВЕРИЛ

	профессор

Васильев Н.И.

Руководитель проекта ________ ________________ /________________/

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Национальный минерально-сырьевой университет «Горный»
		УТВЕРЖДАЮ Заведующий кафедрой   /проф.Васильев Н.И./   "___"__________2010 г.

Кафедра БС

(наименование кафедры)

КУРСОВАЯ РАБОТА

	Математические методы в бурении

По дисциплине _________________________

_______

^{(наименование учебной дисциплины согласно учебному плану)}

ЗАДАНИЕ

Студенту группы РТ-10 _ _Рыжиков С.В.

^{(шифр группы) (Ф.И.О.)}

1. Тема работы Использование современной компьютерной техники и программного обеспечения для решения прикладной задачи из инженерно-буровой

практики

2. Исходные данные к работе Исходные данные содержатся в методических указаниях по курсовой работе

3. Содержание пояснительной записки Требования к содержанию пояснительной записки изложены в методических указаниях

4. Перечень графического материала Блок-схемы алгоритмов и рисунки, необходимые для понимания излагаемого материала

5.Срок сдачи законченной работы ______________

		Васильев Н.И.
	профессор

Руководитель проекта _________ ________________ /_______________/

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: ___________________

АННОТАЦИЯ

Современная компьютерная техника позволяет с высокой точностью решать сложные инженерные задачи, производить оценки выборок, анализировать полученные данные и т.д.

Данная пояснительная записка содержит отчет о выполнении курсовой работы по дисциплине "Математические методы в бурении", которая в свою очередь содержит пять расчетно-графических заданий.

Цель данной работы - научиться проводить математический анализ при буровых процессах, качественно оценить данную ситуацию и составить план решения.

THE SUMMARY

Modern computer technology makes it possible to accurately solve complex engineering problems, to produce estimates of samples, analyze the data, etc.
This explanatory note contains a report on the implementation of the course work in the discipline "Mathematical Methods in the drilling," which, in turn, contains five calculation and graphic assignments.
The aim of this work - to learn to perform mathematical analysis in the drilling process, a qualitative assessment of the situation and plan solutions.

Содержание.

Введение. 5

1. Определение основных статистических оценок выборки. 6

1.1 Среднее арифметическое выборки. 6

1.2 Дисперсия. 6

1.3 Среднеквадратическое отклонение. 6

1.4 Коэффициент вариации V.. 7

1.5 Отбраковка по критерию Шовене. 7

1.6 Правило «трёх сигм». 7

1.7 Интервальная оценка параметров выборки. 7

1.8 Необходимое и достаточное количество экспериментов. 8

1.9 Проверка закона распределения. 8

1.10 Группировка данных. 9

2. Оценка значимости различия средних значений двух выборок. 11

3. Применение методов наименьших квадратов. 14

4. Множественный регрессионный анализ. 17

5. Оценка влияния двух реагентов на предельное напряжение сдвига бурового раствора. 20

Вывод. 26

Список литературы. 27

Введение.

При введении экспериментов необходимо проводить математический анализ, чтобы узнать точность измерений, определить погрешность полученной информации, соблюдены ли были все правила эксперимента, найти ошибки при проведении экспериментов.

Для того, чтобы овладеть основами такого сложного математического анализа, нужно попробовать его провести на готовых примерах, т.е. решить несколько расчетно-графических заданий.

Определение основных статистических оценок выборки.

Исходные данные

Таблица №.1. Исходные данные.

201,24	203,56	207,38	208,82	213,57
199,70	201,61	194,13	208,41	204,38
203,32	191,89	206,83	186,90	196,07
203,49	193,14	178,13	207,77	198,69
206,99	196,10	211,01	205,70	205,19
182,08	206,37	198,81	202,11	189,98
200,09	200,59	191,52	193,93	203,72
207,14	214,49	198,54	192,18
192,04	205,24	197,69	199,51
197,21	189,76	208,78	206,02
201,39	189,82	195,98	196,30

Определение основных статистических оценок выборки

Среднее арифметическое выборки

Среднее значение – это среднеарифметическое из всех измеренных значений:

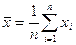, (1.1.1)

где 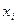- значение случайной величины, n – количество случайной величины;

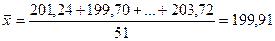
Дисперсия

Мерой отклонения случайной величины от средних значений служит дисперсия и среднеквадратическое отклонение. Дисперсия – это число, равное среднему квадрату отклонений значений случайной величины от её среднего значения:

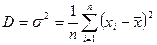, (1.2.1)

где D – дисперсия.