Теплоотдача при свободном движении жидкости
Большую роль как в технике, так и в быту играют процессы теплообмена при естественной конвекции, возникающей из-за разности плотностей нагретых и холодных частиц. Характерная картина свободного движения жидкости вдоль горячей вертикальной поверхности показана на рис. 7.1.
 Нагреваясь у поверхности высотой h (tc>tж) жидкость, вследствие уменьшения ее плотности, поднимается вверх. Слой нагретой движущейся жидкости (δ) является одновременно гидродинамическим и тепловым пограничным слоем, т.к. в пределах этого слоя изменяется скорость (от нуля на стенке до максимума и снова до нуля на границе с неподвижной жидкостью) и температура от (tc до tж.).
Нагреваясь у поверхности высотой h (tc>tж) жидкость, вследствие уменьшения ее плотности, поднимается вверх. Слой нагретой движущейся жидкости (δ) является одновременно гидродинамическим и тепловым пограничным слоем, т.к. в пределах этого слоя изменяется скорость (от нуля на стенке до максимума и снова до нуля на границе с неподвижной жидкостью) и температура от (tc до tж.).
Вначале толщина пограничного слоя мала и ее течение носит ламинарный характер. Постепенно в движение увлекается все большее количество жидкости, толщина ламинарного слоя растет, затем он разрушается (переходный режим) и возникает турбулентный режим течения жидкости. При ламинарном режиме коэффициент теплоотдачи с увеличением толщины пограничного слоя (δ) уменьшается (рис. 7.1), при переходном режиме – резко возрастает и далее, при турбулентном режиме, по высоте поверхности сохраняется постоянным.
На основе математического описания процесса конвективного теплообмена при естественной конвекции выявлена структура уравнения подобия
| Nu=f(Gr, Pr), | (7.1) |
а в результате экспериментального исследования теплоотдачи установлено, что при 103<(Grжх∙Prж) 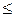 109 – ламинарный режим течения жидкости в пограничном слое;
109 – ламинарный режим течения жидкости в пограничном слое;
(Grжх∙Prж) 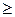 6∙1010 – турбулентный режим;
6∙1010 – турбулентный режим;
109<(Grжх∙Prж) 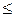 1010 – переходный режим.
1010 – переходный режим.
Число Грасгофа рассчитывается по формуле
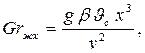 | (7.2) |
где 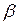 - температурный коэффициент объемного расширения,
- температурный коэффициент объемного расширения, 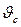 = tc - tж . Для капельных жидкостей значения
= tc - tж . Для капельных жидкостей значения 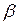 =f(t) приводятся в справочной литературе, для газов – рассчитываются по формуле
=f(t) приводятся в справочной литературе, для газов – рассчитываются по формуле
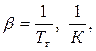 |
полученной на основе совместного решения уравнений
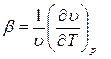 и и 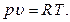 |
Числа Прандтля, 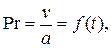 зависящие только от теплофизических свойств жидкостей, приводятся для различных теплоносителей (жидкостей, газов) в справочной литературе.
зависящие только от теплофизических свойств жидкостей, приводятся для различных теплоносителей (жидкостей, газов) в справочной литературе.
При расчетах произведения (Grжх∙Prж) определяющей температурой является температура жидкости (tж), определяющим размером – координата х.
Для расчета коэффициентов теплоотдачи рекомендуются следующие уравнения:
· При ламинарном режиме, 103<(Grжх∙Prж) 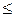 109, локальные коэффициенты теплоотдачи (
109, локальные коэффициенты теплоотдачи ( 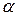 ), описываемые кривой
), описываемые кривой 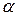 =f(x), рис.7.1, в ламинарной области пограничного слоя, рассчитываются по уравнению
=f(x), рис.7.1, в ламинарной области пограничного слоя, рассчитываются по уравнению
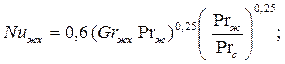 | (7.3) |
средние коэффициенты теплоотдачи 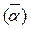 на участке поверхности высотой ℓ с ламинарным течением в пограничном слое – по уравнению
на участке поверхности высотой ℓ с ламинарным течением в пограничном слое – по уравнению
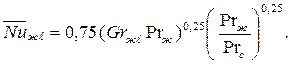 | (7.4) |
· При турбулентном режиме, (Grжх∙Prж)>6 1010, коэффициенты теплоотдачи рассчитываются по уравнению
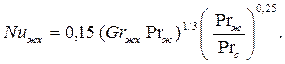 | (7.5) |
· При переходном режиме, 109<(Grжх∙Prж)<6∙1010, средний коэффициент теплоотдачи можно определить по формуле
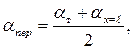 | (7.6) |
где 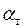 рассчитывается по уравнению (7.5),
рассчитывается по уравнению (7.5), 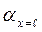 - по (7.3).
- по (7.3).
Коэффициент теплоотдачи зависит от направления теплового потока, и обусловлено это неодинаковыми средними температурами жидкости вблизи поверхности при нагреве жидкости (tc>tж) и при охлаждении (tc<tж), а также зависимостью теплофизических свойств жидкости от ее температуры. Как следствие этого, коэффициент теплоотдачи капельных жидкостей при нагреве больше, чем при охлаждении. Влияние указанного фактора учитывается в уравнениях подобия сомножителем (Prж /Prc)0,25.
При нагреве жидкости (tc>tж) — (Prж /Prc)0,25>1, при охлаждении
(tc<tж) — (Prж /Prc)0,25<1. Числа Prж и Prc берутся из справочных таблиц для жидкости в первом случае – по tж, во втором — по tс.
Для газов с достаточной точностью можно считать, что сомножитель
(Prж /Prc)0,25=1.
Форма поверхности при естественной конвекции жидкости играет второстепенную роль (важна ее протяженность), поэтому по вышеприведенным формулам рассчитывается теплоотдача от плоских, цилиндрических или иной формы вертикальных поверхностей.
Приведенные выше формулы применимы и для горизонтальных плит, но в этом случае вычисленный коэффициент теплоотдачи надо увеличить на 30%, если теплоотдающая поверхность плиты обращена вверх, и уменьшить на 30%, если теплоотдающая поверхность обращена вниз. В качестве определяющего размера берется меньшая сторона плиты.
Для горизонтальных труб, если103<(Grжd∙Prж) 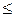 109, для расчета средних коэффициентов теплоотдачи рекомендуется следующее уравнение:
109, для расчета средних коэффициентов теплоотдачи рекомендуется следующее уравнение:
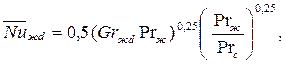 | (7.7) |
определяющий размер – наружный диаметр трубы (d).
Рассмотренная картина движения жидкости относится к случаям, когда расположение и размеры поверхностей, замыкающих среду, на развитие свободного движения не влияют. Такое движение называется свободной конвекцией в большом объеме.
Естественная конвекция в ограниченном объемехарактеризуется наличием восходящих и нисходящих потоков, когда условия свободного движения жидкости значительно отличаются от ее движения в неограниченном пространстве.
Примеры естественной конвекции жидкости в ограниченном объеме представлены на рис. 7.2
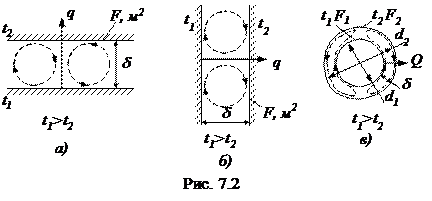 |
а) горизонтальная прослойка жидкости или газа;
б) вертикальная прослойка;
в) цилиндрическая (или сферическая) прослойка
Через газовые прослойки передача теплоты между поверхностями осуществляется тремя способами: теплопроводностью, конвекцией и излучением,через прослойки капельной жидкости – двумя: теплопроводностью и конвекцией. Во всех случаях передачу теплоты рассчитывают по формулам теплопроводности, но коэффициент теплопроводности среды заменяют эквивалентным, учитывающим перенос теплоты другими способами.
Для плоских прослоек тепловой поток рассчитывают по уравнению
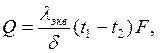 Вт, Вт, | (7.8) |
для цилиндрических
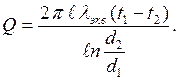 | (7.9) |
Для прослоек капельной жидкости
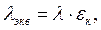 | (7.10) |
где λ –коэффициент теплопроводности жидкости; εк – коэффициент, учитывающий перенос тепла конвекцией.
Для прослоек любой формы при (Grжδ ∙Prж)>103 коэффициент конвекции рассчитывается по формуле
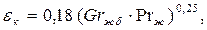 | (7.11) |
где 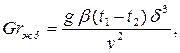 определяющая температура
определяющая температура 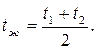
При (Grжδ∙Prж)<103 принимают εк=1.
Для газовых плоских прослоек
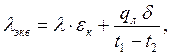 | (7.12) |
где qл, Вт/м2 – плотность теплового потока, передаваемого излучением через газовую прослойку.
Для газовых цилиндрических прослоек
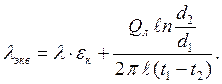 | (7.13) |
7.2. Теплоотдача при продольном омывании поверхности
вынужденным потоком жидкости
Вынужденное течение жидкости (вынужденная конвекция) возникает под действием разности давлений, которая в совокупности с теплофизическими свойствами определяет скорость движения жидкости w0. Таким образом, при вынужденном движении определяющими числами подобия являются число Рейнольдса (Re), включающее в себя скорость w0, и число Прандтля (Pr), зависящее от теплофизических свойств жидкости,
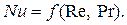 |
В некоторых случаях при малых скоростях и больших температурных напорах (tc-tж) на вынужденное течение жидкости могут накладываться токи естественной конвекции, и тогда
| Nu=f(Re, Gr, Pr). |
Рассмотрим участок поверхности, имеющий температуру tc и омываемый потоком жидкости с температурой tж и скоростью w0. Вблизи поверхности формируется гидродинамический пограничный слой (δ) с ламинарным, переходным и турбулентным режимами течения (рис. 7.3)
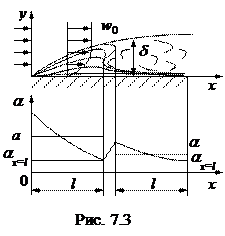 Режим течения в гидродинамическом пограничном слое определяется числом Рейнольдса
Режим течения в гидродинамическом пограничном слое определяется числом Рейнольдса 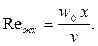
При Reжх<104 – ламинарный режим;
при Reжх>4∙106 – турбулентный;
при 104 <Reжх<4∙106 – переходный.
Для переходного режима из-за неустойчивого течения, характеризуемого частой сменой во времени ламинарного и турбулентного режимов, отсутствует методика расчета коэффициентов теплоотдачи, поэтому его исключают и считают, что
при Reжх 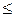 5∙105 – ламинарный режим в пограничном слое;
5∙105 – ламинарный режим в пограничном слое;
при Reжх>5∙105 – турбулентный режим.
В учебной литературе для вынужденного течения жидкости около поверхности приводится вывод интегральных уравнений для теплового и гидродинамического пограничных слоев:
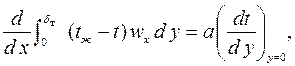 | (7.14) |
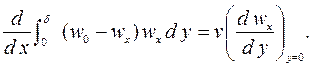 | (7.15) |
Если воспользоваться этими уравнениями для ламинарного и турбулентного режимов течения в пограничном слое, то удается аналитически получить расчетные уравнения для коэффициентов теплоотдачи, которые хорошо согласуются с экспериментальными данными.
Вот эти уравнения для расчета локальных коэффициентов теплоотдачи:
– при ламинарном режиме течения жидкости в пограничном слое
| Nuх=0,33 Reх0,5∙ Pr0,33, | (7.16) |
– при турбулентном режиме
| Nuх=0,0296 Reх0,8∙ Pr0,43. | (7.17) |
Если подставить значения чисел подобия в (7.16),
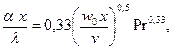 |
и определить зависимость 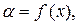 обозначив постоянной С все величины, кроме координаты х,
обозначив постоянной С все величины, кроме координаты х,
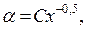 | (7.18) |
то можно найти средний коэффициент теплоотдачи для участка поверхности длиной  с ламинарным течением в пограничном слое по формуле
с ламинарным течением в пограничном слое по формуле
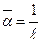 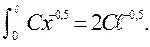 | (7.19) |
Сравнивая (7.18) и (7.19), видим, что средний коэффициент теплоотдачи в
2 раза больше, чем локальный при х=  , т.е.
, т.е.
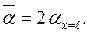 |
Аналогичный анализ уравнения (7.17) дает, что
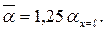
Графическое подтверждение см. на рис. 7.3. Коэффициент теплоотдачи при ламинарном режиме течения жидкости в пограничном слое с увеличением х убывает более резко, чем при турбулентном режиме.
Таким образом, теоретические и экспериментальные исследования позволили получить следующие уравнения для расчета средних коэффициентов теплоотдачи для участка поверхности длиной  при наличии ламинарного пограничного слоя (Reжℓ
при наличии ламинарного пограничного слоя (Reжℓ 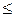 5∙105):
5∙105):
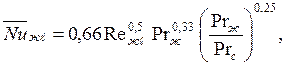 | (7.20) |
турбулентного пограничного слоя (Reжℓ >5∙105):
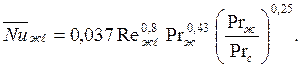 | (7.21) |
Форма поверхности (плоская, цилиндрическая или иная) при продольном омывании её вынужденным потоком жидкости не влияет на коэффициент теплоотдачи.
7.3. Теплоотдача при вынужденном течении жидкости
в трубах и каналах
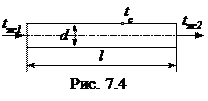 |
При течении в трубе (рис. 7.4) жидкость может нагреваться или охлаждаться.
 |
При нагреве:
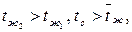 где
где 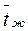 - средняя температура жидкости на участке трубы длиной
- средняя температура жидкости на участке трубы длиной  (рис. 7.5). При охлаждении:
(рис. 7.5). При охлаждении: 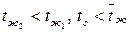 (рис.7.6).
(рис.7.6). Уравнение теплового балансадля отрезка трубы длиной ℓ при нагреве жидкости
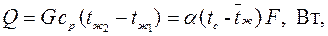 | (7.22) |
при охлаждении жидкости
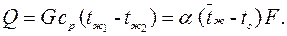 | (7.23) |
Здесь 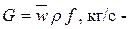 расход жидкости;
расход жидкости; 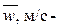 средняя по сечению трубы скорость; ρ, кг/м3, ср, Дж/кг∙К – плотность и теплоемкость жидкости; f=πd2/4, м2 – площадь поперечного сечения трубы; d, м – внутренний диаметр трубы;
средняя по сечению трубы скорость; ρ, кг/м3, ср, Дж/кг∙К – плотность и теплоемкость жидкости; f=πd2/4, м2 – площадь поперечного сечения трубы; d, м – внутренний диаметр трубы;
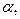 Вт/м2∙К – коэффициент теплоотдачи между поверхностью трубы и жидкостью; F= πd
Вт/м2∙К – коэффициент теплоотдачи между поверхностью трубы и жидкостью; F= πd  , м2 – площадь поверхности теплообмена между жидкостью и трубой.
, м2 – площадь поверхности теплообмена между жидкостью и трубой.
Расчет средней температуры жидкости ( 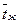 ).
).
Если через Δt΄и Δt" обозначить средние температурные напоры на входе и на выходе из трубы (рис.7.5 и 7.6), то средний температурный напор вычислится по формуле
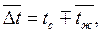 |
откуда средняя температура жидкости
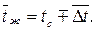 | (7.24) |
При 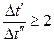 средний температурный напор вычисляется как средний логарифмический
средний температурный напор вычисляется как средний логарифмический
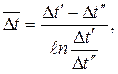 |
при 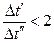 среднюю температуру жидкости можно вычислить как среднюю арифметическую по формуле
среднюю температуру жидкости можно вычислить как среднюю арифметическую по формуле
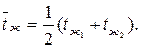 | (7.25) |
Теплоотдачапри вынужденном течении жидкости в трубах зависит от режима течения (ламинарного, турбулентного, переходного), который определяется числом Рейнольдса, 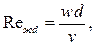 где d - внутренний диаметр трубы, определяющая температура – tж.
где d - внутренний диаметр трубы, определяющая температура – tж.
При Reжd < 2300 режим течения ламинарный, при Reжd>104 устанавливается устойчивый турбулентный режим. В области 2300<Reжd <104 – переходный режим, когда могут сосуществовать ламинарный и турбулентный режимы.
При ламинарном изотермическом течении в любом сечении стабилизированного потока жидкости распределение скоростей представляет собой квадратичную параболу. При этом средняя скорость жидкости равна половине максимальной, которая приходится на ось потока.
При турбулентном режиме основное изменение скорости происходит в вязком подслое, а в ядре потока скорость жидкости по всему сечению практически одинакова.
Указанные распределения скоростей устанавливаются на определенном расстоянии от входа в трубу, которое называется участком гидродинамической стабилизации, или начальным участком (  н).
н).
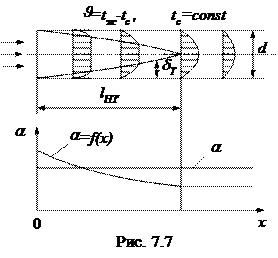 Наряду с участком гидродинамической стабилизации при неизотермическом течении (tc
Наряду с участком гидродинамической стабилизации при неизотермическом течении (tc 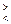 tж),
tж),
рис. 7.7, существует участок тепловой стабилизации (  нт), на котором теплообмен между жидкостью и стенкой трубы осуществляется только в пределах теплового пограничного слоя (δт), а в центральной части потока сохраняется постоянная температура, равная температуре жидкости на входе в трубу.
нт), на котором теплообмен между жидкостью и стенкой трубы осуществляется только в пределах теплового пограничного слоя (δт), а в центральной части потока сохраняется постоянная температура, равная температуре жидкости на входе в трубу.
При смыкании теплового пограничного слоя (δт) в теплообмене начинает участвовать весь поток жидкости.
С увеличением толщины теплового пограничного слоя на начальном термическом участке коэффициент теплоотдачи уменьшается.
За пределами начального термического участка, когда толщина теплового пограничного слоя становится равной радиусу трубы (δт=d/2=const), коэффициент теплоотдачи сохраняет постоянное значение (рис. 7.7). Длина участка тепловой стабилизации при турбулентном режиме  нт
нт 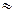 50d.
50d.
На участке гидродинамической стабилизации (  н) и за его пределами характер изменения коэффициента теплоотдачи аналогичный. Уменьшение коэффициента теплоотдачи (
н) и за его пределами характер изменения коэффициента теплоотдачи аналогичный. Уменьшение коэффициента теплоотдачи ( 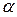 ) с увеличением х на начальном участке объясняется уменьшением средней скорости по сечению трубы, а постоянство коэффициента теплоотдачи за пределами начального участка – установлением стабилизированного распределения скорости.
) с увеличением х на начальном участке объясняется уменьшением средней скорости по сечению трубы, а постоянство коэффициента теплоотдачи за пределами начального участка – установлением стабилизированного распределения скорости.
Увеличение среднего коэффициента теплоотдачи ( 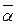 ), рис.7.7., для трубы длиной
), рис.7.7., для трубы длиной  за счет более высокого
за счет более высокого 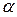 на участках гидродинамической и термической стабилизации учитывается в уравнениях подобия специальным коэффициентом εℓ>1. Для длинных труб εℓ=1.
на участках гидродинамической и термической стабилизации учитывается в уравнениях подобия специальным коэффициентом εℓ>1. Для длинных труб εℓ=1.
При ламинарном неизотермическом течении ( 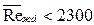 ) жидкости в трубе различают два режима: вязкостный и вязкостно–гравитационный.
) жидкости в трубе различают два режима: вязкостный и вязкостно–гравитационный.
Вязкостный режим характерен для течения вязких жидкостей (маслоохладителей, подогревателей мазута и т.д.) в трубах малого диаметра с высокой скоростью при небольших температурных напорах (tc-tж).
Расчет средних коэффициентов теплоотдачи при вязкостном режиме производят по уравнению
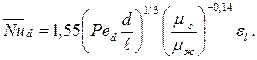 | (7.26) |
Здесь: Ре=Re∙Pr=wa/v – число Пекле; 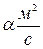 ,– коэффициент температуропроводности; μ, Па∙с – коэффициент динамической вязкости;
,– коэффициент температуропроводности; μ, Па∙с – коэффициент динамической вязкости;
d,  – внутренний диаметр и длина трубы;
– внутренний диаметр и длина трубы; 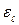 - поправка на начальный гидродинамический участок. При
- поправка на начальный гидродинамический участок. При 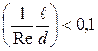 поправочный коэффициент рассчитывается по уравнению
поправочный коэффициент рассчитывается по уравнению
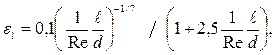 |
при 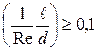 поправочный коэффициент не учитывается (
поправочный коэффициент не учитывается ( 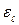 =1).
=1).
Определяющей температурой в уравнении (7.26) является средняя температура жидкости для участка трубы длиной 
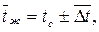 |
где 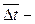 средний логарифмический температурный напор.
средний логарифмический температурный напор.
Вязкостно-гравитационный режим характерен для течения невязких жидкостей в трубах большого диаметра при невысоких скоростях и значительных температурных напорах (tc-tж). В этом случае из-за разностей плотностей различных слоев жидкости на вынужденное движение накладывается свободное движение, которое турбулизирует ламинарный поток. Структура уравнения подобия в этом случае
| Nu=f(Re, Gr, Pr). |
Влияние естественной конвекции сказывается при (Grжd∙Prж) 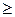 8∙105 и для ориентировочных расчетов средних коэффициентов теплоотдачи при вязкостно-гравитационном режиме (Reжd<2300, (Grжd∙Prж)
8∙105 и для ориентировочных расчетов средних коэффициентов теплоотдачи при вязкостно-гравитационном режиме (Reжd<2300, (Grжd∙Prж) 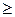 8∙105) рекомендуется формула
8∙105) рекомендуется формула
Nuжd =0,15 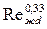 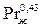 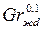 ( Prж /Prc)0,25 ( Prж /Prc)0,25 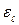 ∙. ∙. | (7.27) |
Определяющей температурой является средняя температура жидкости в трубе ( 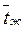 ). Коэффициент
). Коэффициент 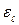 учитывает влияние участка тепловой стабилизации. При
учитывает влияние участка тепловой стабилизации. При  / d
/ d 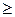 50
50 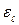 =1, для коротких труб он имеет следующие значения:
=1, для коротких труб он имеет следующие значения:
 /d 1 2 5 10 15 20 30 40
/d 1 2 5 10 15 20 30 40
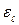 1,9 1,7 1,44 1,28 1,18 1,13 1,05 1,02.
1,9 1,7 1,44 1,28 1,18 1,13 1,05 1,02.
При Reжd < 2300 и (Grжd∙Prж)<5∙108 режим течения жидкости в трубе является вязкостным.
При Reжd>104 наступает стабилизированное турбулентное течение жидкости.
Для расчета среднего по длине трубы коэффициента теплоотдачи при турбулентном течении жидкости рекомендуется уравнение
Nuжd=0,021 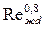 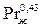 ( Prж /Prc)0,25∙ ( Prж /Prc)0,25∙ 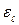 . . | (7.28) |
Определяющей температурой является средняя температура жидкости. Поправочный коэффициент 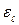 для коротких труб (
для коротких труб (  /d<50) выбирается из табл.7.1.
/d<50) выбирается из табл.7.1.
Таблица 7.1
| Reжd |  /d /d | ||||||
| 1∙104 | 1,65 | 1,5 | 1,34 | 1,23 | 1,13 | 1,07 | 1,03 |
| 2∙104 | 1,51 | 1,4 | 1,27 | 1,18 | 1,10 | 1,05 | 1,02 |
| 5∙104 | 1,34 | 1,27 | 1,18 | 1,13 | 1,08 | 1,04 | 1,02 |
| 10∙104 | 1,28 | 1,22 | 1,15 | 1,10 | 1,06 | 1,03 | 1,02 |
| 100∙104 | 1,14 | 1,11 | 1,08 | 1,05 | 1,02 | 1,02 | 1,02 |
При  / d ≥ 50 εℓ=1.
/ d ≥ 50 εℓ=1.
Для переходного режима (2300<Reжd<104) течения жидкости в трубах характерна периодическая смена ламинарного и турбулентного течений. Ориентировочные значения среднего коэффициента теплоотдачи можно определить по формуле (7.28), если ввести в нее поправочный коэффициент εпер<1. В зависимости от числа Re этот коэффициент принимает следующие значения:
Reжd 2300 3000 5000 6000 8000 10 000
εпер 0,4 0,57 0,72 0,81 0,96 1,0.
Теплоотдача при вынужденном течении жидкости в каналах некруглого сечения рассчитывается по вышеприведенным уравнениям для труб. Определяющим размером в этих уравнениях является эквивалентный диаметр, который рассчитывается по формуле
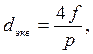 | (7.29) |
где f, м2 – площадь поперечного сечения канала; р, м – периметр этого сечения.
Для каналов кольцевого сечения (труба в трубе), рис.7.8, средний коэффициент теплоотдачи ( 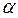 ) от наружной поверхности внутренней трубы к жидкости в кольцевом зазоре рассчитывается по уравнению
) от наружной поверхности внутренней трубы к жидкости в кольцевом зазоре рассчитывается по уравнению
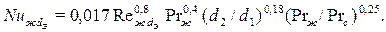 | (7.30) |
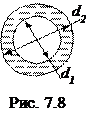 Определяющий размер – эквивалентный диаметр, в соответствии с (7.29),
Определяющий размер – эквивалентный диаметр, в соответствии с (7.29),
dэ=d2-d1.
В изогнутых трубах (змеевиках) коэффициент теплоотдачи увеличивается из-за вторичной циркуляции жидкости под действием центробежных сил. Расчет коэффициентов теплоотдачи в таких трубах выполняется по формулам, полученным для прямых труб, но найденное значение коэффициента теплоотдачи умножается на поправочный коэффициент
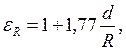 |
где d – диаметр трубы, R – радиус змеевика.
В шероховатых трубах при турбулентном режиме течения, если высота шероховатостей соизмерима с толщиной ламинарного подслоя, происходит разрушение и турбулизация последнего. Это существенно увеличивает теплоотдачу. Для увеличения коэффициента теплоотдачи в трубах выгоднее увеличивать шероховатость, чем скорость. Расчеты показывают, что для увеличения коэффициента теплоотдачи в 2 раза путем увеличения скорости мощность на прокачку теплоносителя увеличивается примерно в 10 раз, а путем увеличения шероховатости – в 3 раза.
Расчет теплоотдачи в шероховатых трубах производится по специальным уравнениям.
