Примеры решения тестовых заданий. Пример 26.Имеются данные по 110 проданным парам обуви: Размер обуви

Пример 26.Имеются данные по 110 проданным парам обуви:

Размер обуви
Число проданных пар

Мода распределения по размеру проданной обуви равна…

Решение 26.Мода, по определению (Определение 7.3), – это наиболее часто встречающееся значение случайной величины. Согласно данных таблицы, мода равна 40.

Пример 27.По данным о 100 проданных пар обуви нашли эмпирическую функцию распределения:

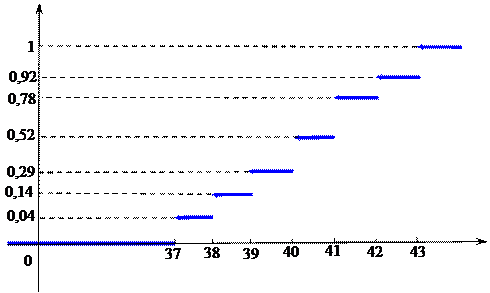
Обуви 39-го размера было продано…

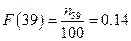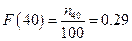Решение 27.По определению эмпирической функции распределения (Определение 7.4) и . Таким образом, обуви размера меньше 39-го, было продано 14 пар, а обуви, размера меньше 40-го, было продано 29 пар. Значит, обуви 39-го размера продано 15 пар.

Пример 28.Произведена выборка 100 роликов. По данным отклонений x от номинального размера их диаметров построена гистограмма частот.

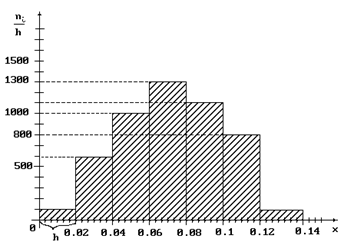
Тогда число роликов, удовлетворяющее неравенству 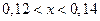, равно…

Решение 28.По данным гистограммы 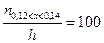. . 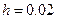Отсюда .

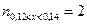Пример 29.Пусть (2, 1, 5, 4, 2, 0, 2, 1) ­– наблюдавшиеся значения выборки. Значение эмпирической функции распределения F(3) равно ...

Решение 29.По определению (Определение 7.4) эмпирической функции распределения 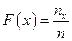. 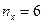, , 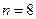поэтому .

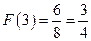Пример 30.По результатам распределения 100 рабочих по тарифным разрядам найдена эмпирическая функция распределения:

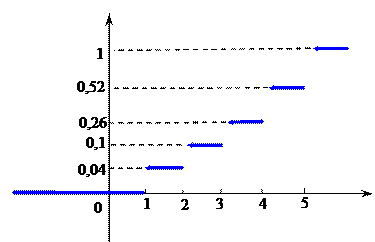
Количество рабочих, имеющих тарифный разряд НИЖЕ ТРЕТЬЕГО, равно...

Решение 30.Событие {«рабочий имеет разряд ниже третьего»}, имеет вероятность 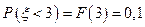. Поскольку опыт проводился 100 раз, количество рабочих, имеющих тарифный разряд НИЖЕ ТРЕТЬЕГО, равно 10.

Тестовые задания для самостоятельного решения

ТЗ 31. Легкое. Пусть (3, 0, 4, 3, 6, 0, 3, 1) - наблюдавшиеся значения выборки. Значение эмпирической функции распределения F(3) равно ...

а) £ 2/8

б) £ 3/8

в) £ 5/8

г) £ 2

д) £ 5

ТЗ 32. Средней трудности. Эмпирическая функция распределения, построенная по 100 наблюдениям, имеет вид

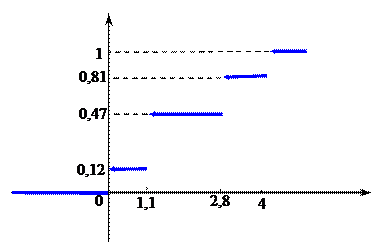
Тогда мода выборочного распределения равна…

а) £ 2,8

б) £ 2

в) £ 1,1

г) £ 4

д) £ 1

ТЗ 33. Трудное. По результатам распределения 100 рабочих по тарифным разрядам найдена эмпирическая функция распределения:

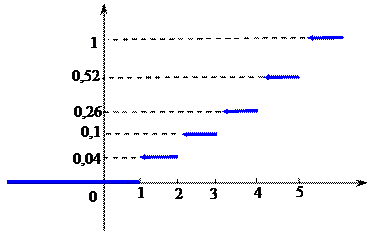
Количество рабочих, имеющих пятый тарифный разряд, равно…

а) £ 54

б) £ 48

в) £ 52

г) £ 4

д) £ 46

ТЗ 34. Повышенной трудности. Произведена выборка 100 роликов. По данным отклонений x от номинального размера их диаметров построена гистограмма частот.

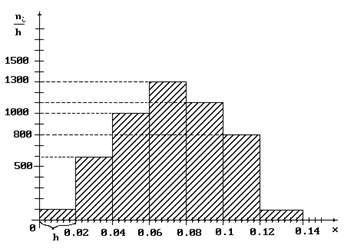
Тогда число роликов, удовлетворяющее неравенству 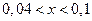, равно…

а) £ 74

б) £ 34

в) £ 26

г) £ 68

д) £ 46

ТЗ 35. Легкое. Пусть X₁, X₂, …, X_n – выборка из распределения Пуассона с неизвестным параметром l. Какая из перечисленных ниже функций НЕ ЯВЛЯЕТСЯ статистикой?

а) £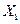

б) £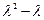

в) £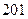

г) £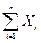

д) £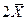

Тема 8. Оценка параметров генеральной совокупности

Основные определения

Определение 8.1.Несмещенная оценка 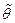для параметра 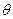– оценка обладающая свойством .

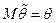Определение 8.2.Состоятельная оценка 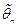для параметра 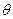– оценка обладающая свойством .

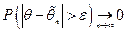Определение 8.3.Эффективная оценка – оценка обладающая наименьшей дисперсией среди всех возможных оценок параметра .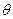

Определение 8.4.Несмещенная и состоятельная оценка математического ожидания: выборочное среднее 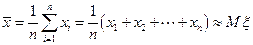. Если ξ распределена нормально, то 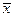является также эффективной оценкой.

Определение 8.5.Несмещенная и состоятельная оценка дисперсии: исправленная выборочная дисперсия .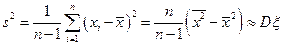

Определение 8.6.Метод моментов – это способ оценивания параметров распределений, при котором теоретические моменты приравниваются к эмпирическим. Например: 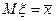или 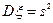.