Примеры решения тестовых заданий. Пример 22.Если случайная величина X задана плотностью распределения
Пример 22.Если случайная величина X задана плотностью распределения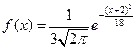 
, то 
…
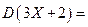Решение 22.Функция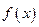 
задает плотность нормального распределения (Определение 6.6). Сопоставляя параметры, мы приходим к выводу, что 
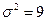. Воспользуемся теперь свойствами дисперсии (Определение 6.4) и представим 
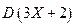в виде 
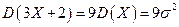. Ответ: 
.
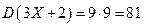Пример 23.График функции распределения случайной величины Х имеет вид:
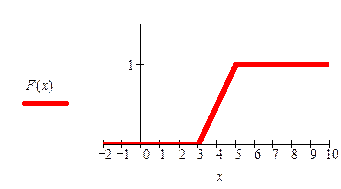
Тогда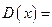 
…
Решение 23.На графике изображена функция равномерного распределения (Определение 6.5) на отрезке [a,b]=[3,5]. По свойствам равномерного распределения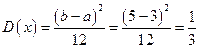 
.
Пример 24.Пусть Ф(x) это функция стандартного нормального распределения. Если Ф(x) = 0,65, то Ф(–x) равно ...
Решение 24.По определению
.
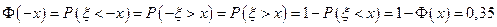Докажем, что если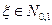 
, то и 
.
.
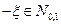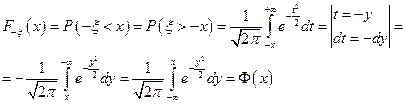Нужно запомнить, что нормально распределенная случайная величина, при смене ее знака с плюса на минус, не меняет своего распределения.
Пример 25.Пусть f(x) это функция стандартного нормального распределения. Если f(x) = 0,84, то f(–x) равно ...
Решение 25.Функция плотности стандартного нормального распределения является четной, поэтому f(–x) = 0,84.
Тестовые задания для самостоятельного решения
ТЗ 26. Легкое. Если случайная величина X задана плотностью распределения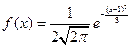 
, то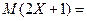 
…
а) £ 5
б) £ 2
в) £ 0
г) £ 3
д) £ 1
ТЗ 27. Средней трудности. Случайная величина X распределена нормально с математическим ожиданием a = 25. Вероятность попадания X в интервал (10, 25) равна 0,2. Вероятность НЕ попадания X в интервал (10, 40) равна ...
а) £ 0,4
б) £ 0,2
в) £ 0
г) £ 0,8
д) £ 0,6
ТЗ 28. Трудное. График плотности распределения случайной величины Х имеет вид:
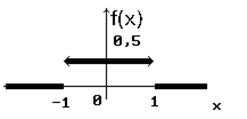
Тогда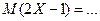 
а) £ 1
б) £ 0
в) £ 0,5
г) £ -1
д) £ 5
ТЗ 29. Повышенной трудности. Если график функции распределения случайной величины Х имеет вид:
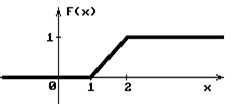
то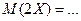 
а) £ 0
б) £ 3
в) £ 1
г) £ 2
д) £ 4
ТЗ 30. Средней трудности. Пусть Ф(x) это функция стандартного нормального распределения. Если Ф(x) = 0,9, то Ф(–x) равно ...
а) £ 0,9
б) £ 0,05
в) £ -0,9
г) £ 0
д) £ 0,1
Тема 7. Статистические методы обработки данных
Основные определения
Определение 7.1.Генеральная совокупность – это все мыслимые результаты вероятностного эксперимента. Например, все население Земли или выпущенные станком ролики за весь период его эксплуатации и т.п.
Определение 7.2.Выборка – это часть генеральной совокупности, отобранная для исследования. Выборка сама по себе не представляет интереса для исследователя. Интерес представляют свойства генеральной совокупности, которые можно узнать изучая выборку. Выборка является результатом вероятностного эксперимента, поэтому говоря о выборке следует иметь ввиду наличие своеобразной метагенеральной совокупности всех возможных выборок из данной генеральной совокупности. По этой причине выводы, сделанные по выборке являются случайными.
Определение 7.3.Мода. Наиболее вероятное значение случайной величины называется ее модой.
Определение 7.4.Эмпирическая функция распределения. Функция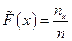 
, где nx – это количество наблюдений строго меньших x, а n – это общее число наблюдений в выборке. Эмпирическая функция распределния (ЭФР) всегда ступенчатая. Согласно закона больших числел при увеличении объема выборки ЭФР стремится к гладкой теоретической функции распределения. В качестве аналогии можно привести правильный многоугольник, который при увеличении числа граней стремится к гладкой окружности.
Определение 7.5.Гистограмма. Эмпирический аналог функции плотности. Отличается тем, что состоит из прямоугольников. Сумма площадей всех прямоугольников равна единице. Высота прямоугольника пропорциональна абсолютной частоте, с которой выборочные значения попадают в интервал, где расположен прямоугольник и обратно пропорциональна ширине данного интервала. Гистограмма выборки неоднозначна, в том смысле, что исследователь в праве сам выбирать ширину интервалов и их границы. При удачном выборе способа построения гистограммы, она может с успехом заменять теоретическую функцию плотности. При построении гистограммы следует следить за тем, чтобы выборочные значения не попадали на границы интервалов.