Моделирование задач оптики
В настоящее время широкое распространение получили приборы, принцип работы которых основан на преобразовании излучения различными типами оптических элементов. К этим приборам относятся фокусаторы, дифракционные решетки, волноводные элементы, элементы градиентной оптики, светоделители, резонаторы и т.д. При конструировании подобных элементов необходимо получать определенный набор параметров, без которых невозможно конструирование и разработка технологических процессов. В общем случае, распространение излучения описывается уравнением Максвелла (1.75 – 1.77). К сожалению, данные уравнения, даже в самом простом виде очень трудно решить численно. Это связано с проблемами точности численных методов.
Как известно, для того, чтобы осуществлялась сходимость сеточного численного метода (например, метода Ньютона) размер сетки должен быть равен 1/4 характерного параметра (1/4 длины волны излучения). Это приводит к резкому увеличению объема памяти используемой компьютером для решения этих задач.
В тоже время, как показывает практика, различные аналитические решения с большой точностью описывают распространение излучения в среде при наличии правильного формирования функции передачи исследуемого объекта. При этом, все практические задачи можно разделить на два класса:
1. Прямые задачи оптики.
2. Обратные задачи оптики.
Прямые задачи оптики формулируются следующим образом – известно поле до объекта, известно как это поле преобразуется объектом, необходимо определить, как это поле записывается приемником излучения. Математически, это записывается следующим образом:
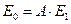 , (3.1)
, (3.1)
где Е0 – параметр поля (напряженность, фаза, интенсивность и т.д.) до объекта;
А – оператор перехода, описывающий изменение поля на объекте, который часто называют передаточной функцией объекта;
Е1 – поле в устройстве регистрации (фотоприемник, экран).
В нашей задаче Е0 и А известны, требуется определить Е1.
Прямые задачи оптики достаточно хорошо решаются, однако, при разработке элементов чаще требуется решение обратных задач оптики, которые можно сформулировать следующим образом – задано поле до объекта, задано поле в приемнике излучения, необходимо подобрать объект, который изменяет это поле заданным образом. В математической постановке – это требование найти оператор А или передаточную функцию объекта.
Данные задачи решаются достаточно сложно и относятся к классу некорректно поставленных задач. Чаще всего для решения подобных проблем применяют следующий прием – разбивают интересующий нас объект на несколько объектов, функция передачи (волновая функция) которых известна или рассчитывается несложным образом. Общая функция передачи этих объектов определяется с помощью законов геометрической оптики и представляет собой матрицу, порядок которой определяется размерностью системы. Таким образом, мы сводим обратные задачи оптики к прямым задачам.
