Напомним ещё раз некоторые определения и результаты.
Если перестановка разлагается в композицию циклов длин 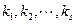 , то говорят, что она имеет тип
, то говорят, что она имеет тип 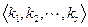 . (Циклы длины 1 соответствуют неподвижным точкам и не учитываются.)
. (Циклы длины 1 соответствуют неподвижным точкам и не учитываются.)
Порядком перестановки 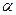 называется такое наименьшее натуральное число
называется такое наименьшее натуральное число 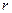 , что
, что 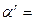 id (здесь id – тождественная перестановка). Мы выяснили, что порядок перестановки типа
id (здесь id – тождественная перестановка). Мы выяснили, что порядок перестановки типа 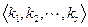 равен наименьшему общему кратному длин циклов
равен наименьшему общему кратному длин циклов 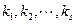 (обозначается: НОК
(обозначается: НОК 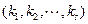 ).
).
Декремент перестановки равен 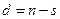 , где
, где 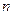 – количество переставляемых элементов, а
– количество переставляемых элементов, а 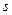 – количество циклов в графе перестановки, включая циклы длины 1.
– количество циклов в графе перестановки, включая циклы длины 1.
Мы установили, что цикл (вернее, циклическая перестановка) чётной длины – нечётен, а цикл нечётной длины – чётен. Мы также установили, что декремент цикла длины 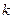 равен
равен 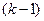 .
.
Преобразования 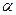 и
и 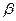 называются сопряжёнными, если их графы изоморфны, т.е. совпадают, отличаясь только нумерацией вершин. Это равносильно тому, что
называются сопряжёнными, если их графы изоморфны, т.е. совпадают, отличаясь только нумерацией вершин. Это равносильно тому, что 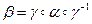 , где
, где 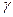 – перестановка, которая сопоставляет номеру каждой вершины графа преобразования
– перестановка, которая сопоставляет номеру каждой вершины графа преобразования 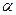 номер соответствующей вершины графа преобразования
номер соответствующей вершины графа преобразования 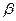 . Говорят, что
. Говорят, что 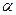 и
и 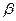 сопряжены при помощи
сопряжены при помощи 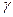 или что
или что 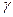 – перестановка, сопрягающая
– перестановка, сопрягающая 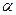 и
и 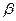 . С другой стороны, изоморфность графов двух перестановок означает как раз, что типы этих двух перестановок одинаковы. При этом ясно, что сопрягающая перестановка переводит вершины каждого цикла в вершины цикла такой же длины, причём с сохранением порядка следования этих вершин.
. С другой стороны, изоморфность графов двух перестановок означает как раз, что типы этих двух перестановок одинаковы. При этом ясно, что сопрягающая перестановка переводит вершины каждого цикла в вершины цикла такой же длины, причём с сохранением порядка следования этих вершин.
Отрицательная и нулевая степени перестановки. По определению, 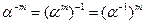 для
для 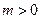 и
и 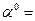 id. Тогда
id. Тогда 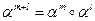 и
и 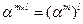 для любых целых
для любых целых 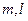 (можете проверить!).
(можете проверить!).
В задаче № 2 мы нашли, что
а) 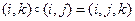 (здесь
(здесь 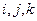 – различные числа),
– различные числа),
б) 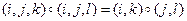 (здесь
(здесь 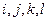 – различные числа).
– различные числа).
В задаче № 3 мы нашли композиции циклов, точнее разложения этих перестановок в композиции циклов с непересекающимися множествами подвижных точек:
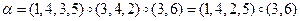
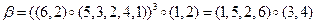 .
.
Эти перестановки чётные, имеют декремент, равный 4.
Поскольку они имеют одинаковый тип 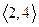 , то они сопряжены. Сопрягающая их перестановка
, то они сопряжены. Сопрягающая их перестановка 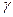 переводит, как было сказано выше, номера вершин для графа перестановки
переводит, как было сказано выше, номера вершин для графа перестановки 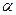 в номера соответствующих вершин для графа перестановки
в номера соответствующих вершин для графа перестановки 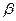 . При этом, номера вершин для цикла длины 4 в графе для
. При этом, номера вершин для цикла длины 4 в графе для 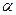 переводятся в номера вершин для цикла той же длины в графе для
переводятся в номера вершин для цикла той же длины в графе для 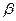 . Пусть, например, 1 переходит в 1. Тогда однозначно определяется, куда переходят номера других вершин этого цикла. Точно так же поступаем с циклами длины 2. Пусть, например, 3 переходит в 3. В итоге, получим такую сопрягающую перестановку:
. Пусть, например, 1 переходит в 1. Тогда однозначно определяется, куда переходят номера других вершин этого цикла. Точно так же поступаем с циклами длины 2. Пусть, например, 3 переходит в 3. В итоге, получим такую сопрягающую перестановку:
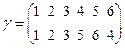
1. А сколько вообще в этой задаче есть таких сопрягающих перестановок? (Ответ: 8.) Выпишите их все.
2. Для следующих перестановок найдите их чётность, декремент, разложения в композицию циклов с непересекающимися множествами подвижных точек и порядок:
а) 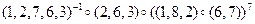
б) 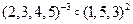
Ответ для разложений: а) 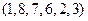 , б)
, б) 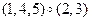 .
.
3. Проверьте, что если имеется разложение перестановки в композицию циклов с непересекающимися множествами подвижных точек, то декремент этой перестановки равен сумме декрементов образующих её циклов.
4. Верна ли формула 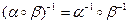 ? Если нет, то как надо её подправить? Ответ обосновать.
? Если нет, то как надо её подправить? Ответ обосновать.
