Напомним определения экстремальных точек и экстремальных значений функций

Глава 5. Исследование функций и построение её графика.

Тема 1 . Исследование функций .

Одной из простейших операций исследования поведения функции является исследование

функции на монотонность.

Определение 1.1.Функция 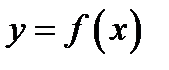, заданная на интервале 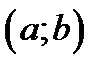,называетсявозрастающейфункцией на этом интервале, если большему значению аргумента 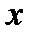соответствует большее значение функции, то есть

(1.1)

Определение 1.2.Функция 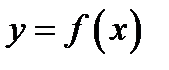, заданная на интервале 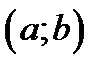,называетсяубывающейфункцией на этом интервале, если большему значению аргумента 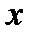соответствует меньшее значение функции, то есть

(1.2)

Убывающие или возрастающие на интервале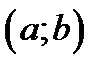функции называются монотонными функциями.

Если задан график функции, то по его виду легко определить возрастает функция или убывает.

Если двигаться по графику слева направо, то у возрастающей функции график поднимается вверх (рис.1а), а у убывающей функции график опускается вниз (рис.1б).

рис.1а. рис.1б.

На рисунках 1а.,1б приведены графики монотонных функций. Рассмотрим график, предложенный

на рис.2

рис.2

Функция не является монотонной на всем множестве. Но на интервале 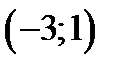она убывает. На интервале 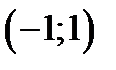она возрастает. И наконец, на интервале 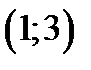она убывает. Итак, если задан график, то несложно определить интервалы, где функция возрастает, а где убывает.

Возникает вопрос, как исследовать функцию на монотонность, если задана только формула, определяющая функцию. В случае, когда функция дифференцируема, это сделать легко.

Пусть на интервале 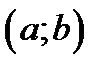задана дифференцируемая функция 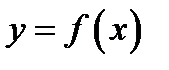. Геометрически это означает, что в каждой точке 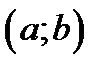график функции имеет касательную. Наклон касательной, как мы уже знаем, зависит от знака производной в точке касания. Если производная больше нуля, то угол наклона касательной острый, если производная меньше нуля угол наклона касательной тупой.

Теорема 1.1.Пусть функция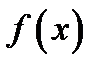определена и непрерывна на 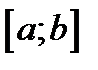, дифференцируема

на 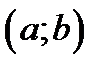и если:

1)

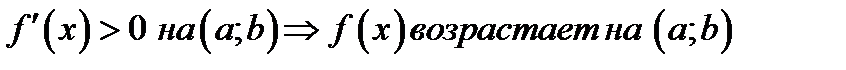
(1.3)

2)

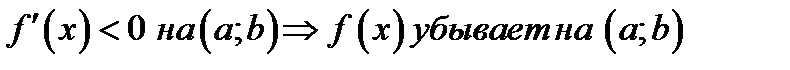
Доказательство. Докажем пункт 1). Как всегда берём любую пару 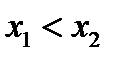из 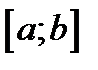. Нужно доказать, что 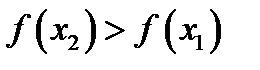. На отрезке 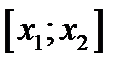выполнены все условия теоремы о среднем Лагранжа. Запишем формулу Лагранжа для этого случая

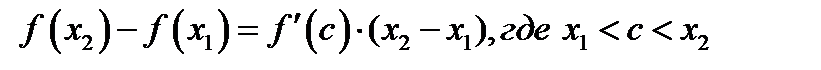(1.4)

Так как

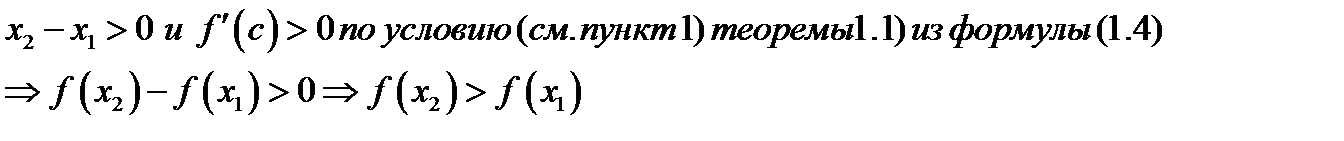
По определению 1.1 это означает, что функция возрастает.

Пункт 1) Теоремы 1.1 доказан. Доказательство пункта 2) предоставляем читателю.

Напомним определения экстремальных точек и экстремальных значений функций.

Локальным максимумом называется значение функции, которое больше чем любое другое значение функции для всех достаточно близких значений аргумента.

Локальным минимумом называется значение функции, которое меньше чем любое другое значение функции для всех достаточно близких значений аргумента.

Локальные максимумы и локальные минимумы называются экстремальными значениями функций или локальными экстремумами.

Значения аргумента, при которых достигаются экстремальные значения функций, называются экстремальными точками. Экстремальные точки всегда лежат внутри интервала. Значения аргументов 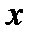, при которых производная функции 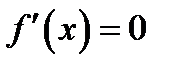или не существует называются критическими точками функции 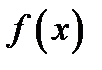. Критические точки всегда лежат внутри интервала. Следующая теорема говорит нам о том, что экстремальные точки нужно искать только среди критических.

Теорема 1.2.Если в точке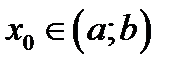имеется локальный экстремум,то эта точкакритическая.Доказательство. 1. Если 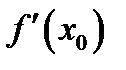не существует, то 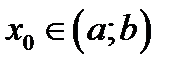критическая точка. Если же в точке

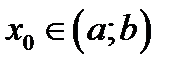производная существует, то в силу условия теоремы 1.2 из теоремы Ферма следует, что 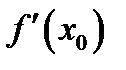=0.

Замечание. Наоборот неверно, если точка 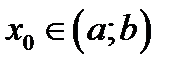критическая, то совсем не обязательно, что она экстремальная.

Рис.3

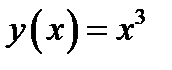Пример 1. . Точка 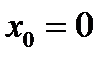критическая так как 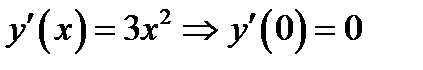. Но если посмотреть на график, то видно, что функция 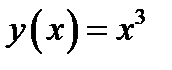в критической точке не имеет экстремума рис 3.

Приведём алгоритм определения экстремальных точек (используются только первые производные).

Правило 1.1 отыскания локальных экстремумов дифференцируемой функции :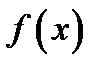

1. Находим критические точки.

2. Из найденных точек 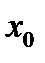оставляем те, при переходе через которые 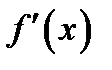меняет знак.

3. Локальный максимум достигается в точках 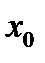, при переходе через которые 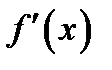меняет знак с положительного значения на отрицательное значение.

4. Локальный минимум достигается в точках 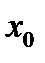, при переходе через которые 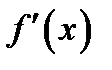меняет знак с отрицательного значения на положительное значение.

5. Замечание. Экстремума нет в тех точках, при переходе через которые 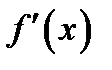не меняет знак.

Рассмотрим поясняющий пример.

Пример 1.1. Определить интервалы монотонности и точки локальных экстремумов

функции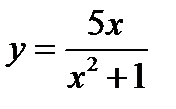

Решение. Вычисляем первую производную функции

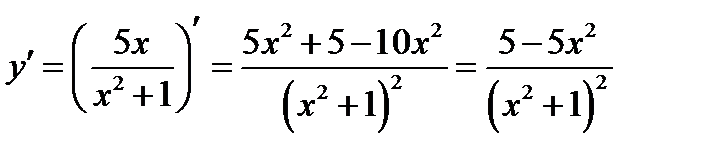
и находим критические точки функции. Так как производная 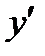существует при любых аргументах 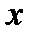. То критическими точками являются точки, в которых производная равна нулю

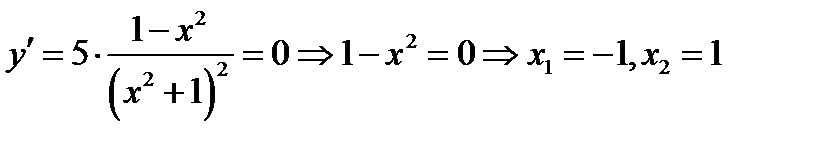
С помощью производной и критических точек исследуем функцию по правилу 1.1

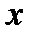		-1
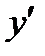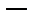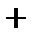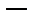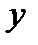		-2.5		2.5

Между критическими точками производная функции всегда сохраняет знак.

Ответ. Согласно правилу 5.1 функция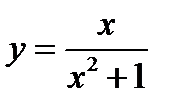

1) на интервале 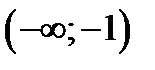убывает, 2) на интервале 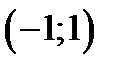возрастает,

3) на интервале 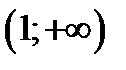убывает.

Согласно правилу 1.1 существования экстремумов

1) точка 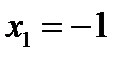является точкой локального минимума. Значение локального минимума равно -2.5.

2) точка 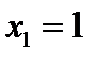является точкой локального максимума. Значение локального максимума равно 2.5.

График функции 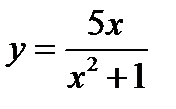можно посмотреть на рисунке 2.

Пример 1.2. Определить интервалы монотонности и точки локальных экстремумов

функции .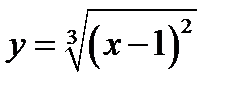

Решение. Вычисляем первую производную функции

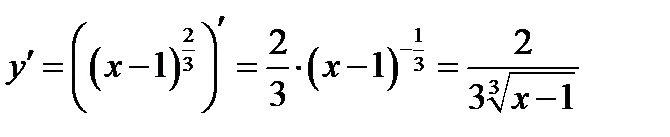
и находим критические точки функции. Так как производная функции нигде не равна нулю, то

критическими могут быть только точки, в которых производная не существует. Такой точкой является точка .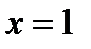

С помощью производной и критических точек исследуем функцию по правилу 1.1

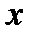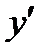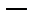		нет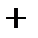

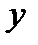Между критическими точками производная функции сохраняет знак.

Ответ. Функция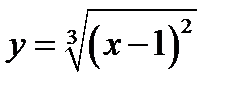

1) на интервале 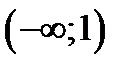убывает, 2) на интервале 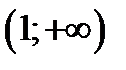возрастает.

Согласно правилу 1.1 существования экстремумов точка 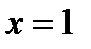является точкой локального минимума. Значение локального минимума равно 0.

На рисунке 4 приведён эскиз графика функции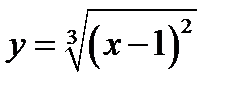

рис.4

С помощью первой производной мы определяли интервалы монотонности дифференцируемых функций и исследовали эти функции на экстремумы.

Определение 1.2.Назовём функцию 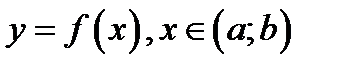дважды непрерывно дифференцируемой, если её вторая производная 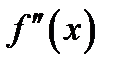непрерывна на .

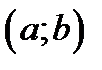Вторая производная используется для исследования графиков дважды непрерывно дифференцируемых функций на выпуклость. Мы будем использовать следующие определения выпуклости вверх и выпуклости вниз.

Определение 1.3.Функция, дифференцируемая на интервале 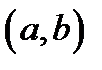, выпукла вверх, если её производная на этом интервале убывает.

Геометрически это означает, что наклон касательной уменьшается.

рис.5

Определение 1. 4.Функция, дифференцируемая на интервале 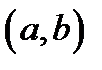, выпукла вниз, если её производная на этом интервале возрастает.

Геометрически это означает, что наклон касательной увеличивается.

рис.6

Теорема 1.3.Пусть функция 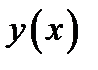дважды дифференцируема на интервале 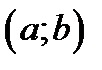тогда, если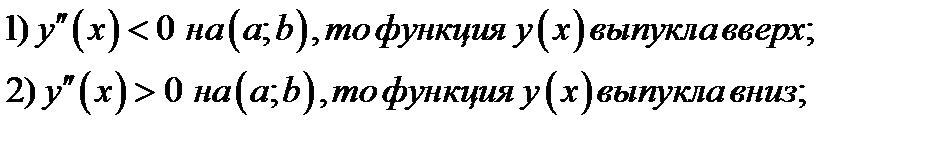

Доказательство. Докажем пункт 1) теоремы 1.3. По условию 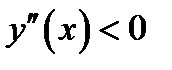, следовательно, по теореме 1.1 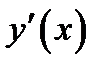убывает. Из определения 1.3 следует, что функция 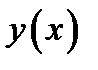выпукла вверх.

Докажем пункт 2) теоремы. По условию 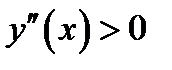, следовательно,по теореме 1.1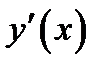

возрастает. Из определения 1.4 следует, что функция 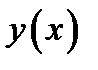выпукла вниз.

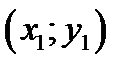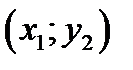Замечание. Как известно, из двух точек с одинаковыми абсциссами и выше

лежит точка, у которой ордината больше и наоборот ниже лежит точка, у которой

ордината меньше.

Теорема 1.4.Точки графика выпуклой вверх дифференцируемой функции 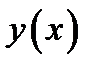лежат нижелюбой касательной проведённой к графику.

Доказательство. Пусть 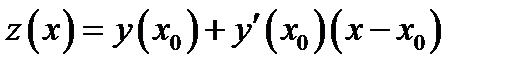уравнение касательной прямой, проведённой к графику функции 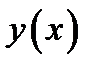в точке касания 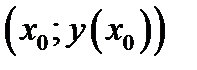. Докажем, что любая точка касательной лежит выше точки графика функции 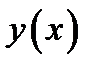(см. замечание выше), то есть 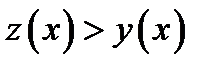для 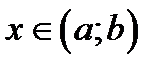. Возьмём точку 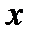справа от точки 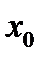, что означает 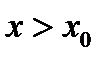. Рассмотрим разность

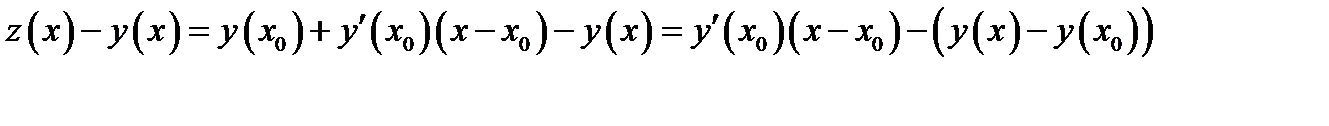
Применим теорему Лагранжа о среднем в дифференцировании к разности 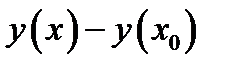, получаем 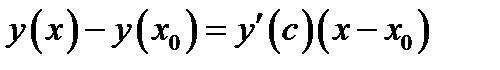. Отсюда , .

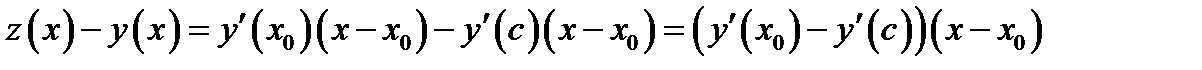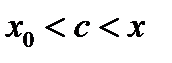По условию у нас производная 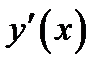функции 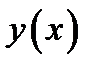убывает. Следовательно, разность

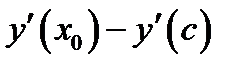положительна. Отсюда следует, что 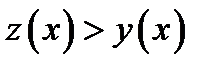и поэтому точка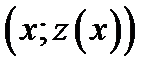

лежит выше точки 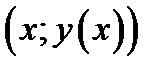. Теорема доказана. Аналогично рассматривается случай, когда

точка .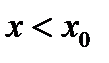

Теорема 1.5.Точки графика выпуклой вниз функции 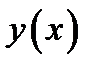лежат вышелюбой касательной проведённой к графику.

Доказательство аналогично доказательству теоремы 1.4.

Определение 1.5.Точка 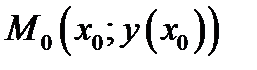, лежащая на графике функции 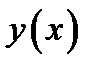, будет точкой перегиба графика функции, если

1) график функции 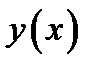имеет в точке 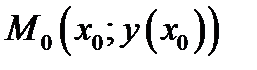касательную прямую

вертикальную или наклонную;

2) слева и справа от точки 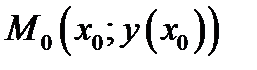выпуклости графика противоположно направлены.

Замечание.В точках перегиба графика функция непрерывна.

Определение 1.6.Назовём точку 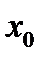, в которой график непрерывен, точкой « подозрительной на перегиб», если в этой точке .

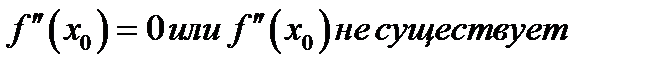Теорема 1.6.Точки перегиба графиков дважды дифференцируемых функций находятся среди

точек « подозрительных на перегиб».

Доказательство. Пусть точка 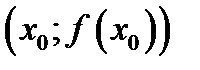является точкой перегиба графика функции. Если значения 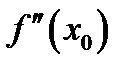не существует, то теорема доказана. Пусть 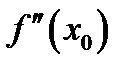существует и по условию слева и справа от точки перегиба графика 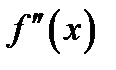имеет разные знаки. Следовательно, в точке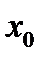 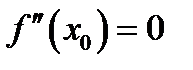(см.в главе 3, теорему4.9 ).

Правило 1.2 нахождения точек перегиба графика функции (используется вторая производная).

Для отыскания точек перегиба графика дважды дифференцируемой функции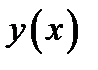

следует:

1. Найти точки, «подозрительные на перегиб».

2. Точка перегиба достигается в тех 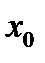, при переходе через которые 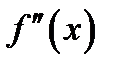меняет знак.

Пример 1.3.Определить интервалы выпуклости и точки перегиба графика функции .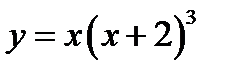

Решение. Вычисляем вторую производную функции

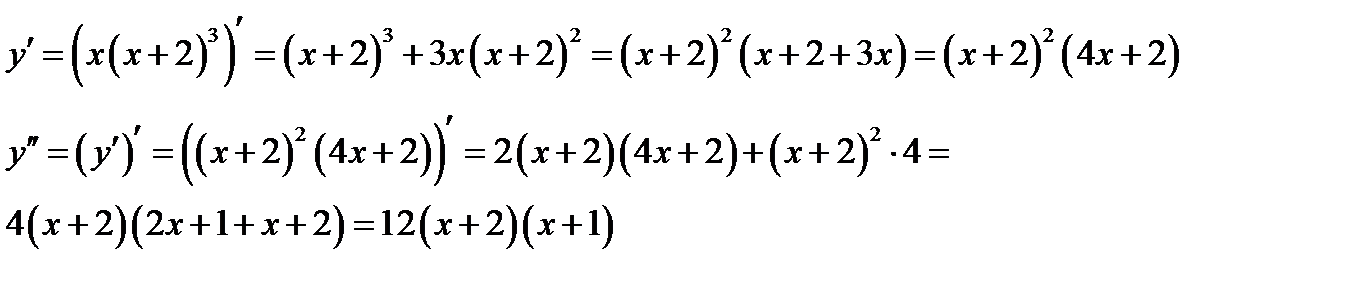
и находим точки подозрительные на перегиб. В этих точках вторая производная равна нулю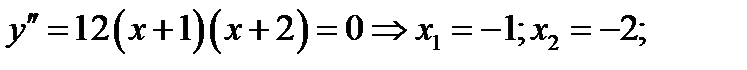

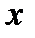		-2		-1
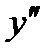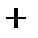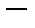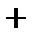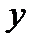				-1

Между критическими точками производная функции сохраняет знак.

Ответ. Функция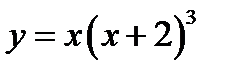

1) на интервале 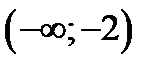выпукла вниз, 2) на интервале 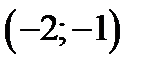выпукла вверх, 3) на интервале 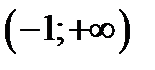выпукла вниз.

Согласно правилу 1.2 существования точек перегиба

1) точка 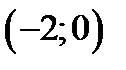является точкой перегиба графика функции.

2) точка 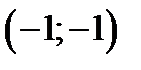является точкой перегиба графика функции.

Пример 1.4.Определить интервалы выпуклости и точки перегиба графика функции .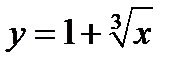

Решение. Вычисляем вторую производную функции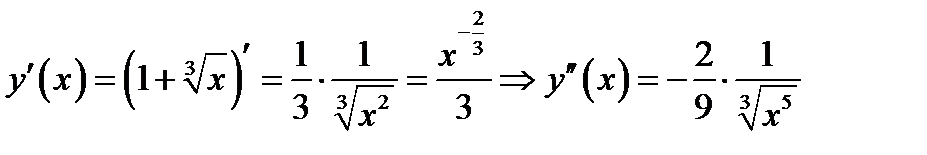

Находим точки « подозрительные на перегиб». В этих точках вторая производная равна нулю или не существует. Дробь равна нулю, если числитель равен нулю. Дробь не существует, если знаменатель равен нулю. В нашем случае только знаменатель равен нулю. Поэтому точкой

« подозрительной на перегиб» является точка .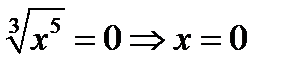

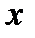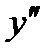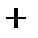		нет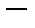

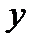Между точками « подозрительными на перегиб» вторая производная функции сохраняет знак.

Ответ. Функция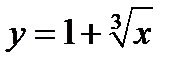

1). на интервале 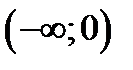выпукла вниз 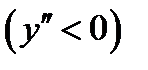, 2) на интервале 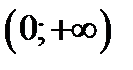выпукла вверх.

Так как касательная в точке 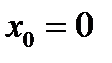является вертикальной прямой, то согласно определению 1.5 точка 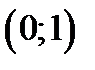является точкой перегиба графика функции см. рис 7.

рис.7