Д) абсолютно заделанный край

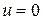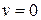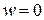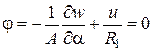, , , . (2.37)

В последнем соотношении 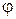– угол поворота нормали координатной поверхности оболочки вокруг касательной к линии .

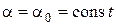2. Неоднородные граничные условия:

А) загруженный край

(2.38)

, ,

, ,

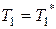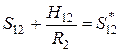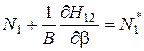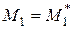где 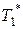, , 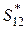, 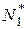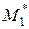– усилия, приложенные к краю (в частном случае некоторые из них могут быть равны нулю).

Б) шарнирный, неподвижно опертый край загружен моментом

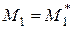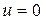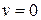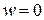, , , ; (2.39)

В) шарнирный, свободный в тангенциальном направлении край загружен моментом и тангенциальной силой

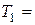
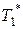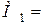
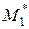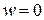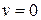, , , ; (2.40)

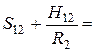
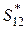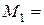
или , , 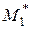, 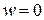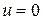; (2.41)

Г) шарнирный, свободный в нормальном направлении край загружен моментом и поперечной силой

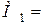
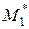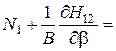
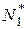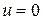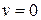, , , ; (2.42)

Д) смещенный край

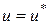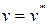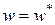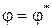, , , , (2.43)

где 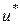, , 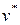, , 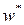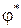– заданные перемещения и угол поворота края оболочки.

Неоднородные граничные условия могут быть и смешанными. В этом случае необходимо следить, чтобы заданные усилия и перемещения не противоречили друг другу.

Аналогичным образом могут быть записаны и граничные условия для края, который определяется координатной линией .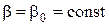

В случае, когда оболочка вовсе не имеет граничного контура (полностью замкнутая оболочка) или граничный контур определяется лишь по линии одной координаты (частично замкнутая оболочка), то граничные условия по направлению замкнутых координат теряют свои обычные формулировки и заменяются условиями периодичности с периодом, обеспечивающим однозначность перемещений в любой точке рассматриваемой замкнутой линии координат.

Приведенные результаты могут быть обобщены на случай сопряжения края рассматриваемой оболочки с каким-либо упругим бортовым элементом (балка, пластина, оболочка и т.д.).

Частные случаи анизотропии материала слоев оболочки

Рассмотрим изменения основных соотношений теории слоистых анизтропных оболочек в частных случаях анизотропии материала их слоев.

Оболочки, составленные из ортотропных слоев.

В этом случае главные направления упругости в каждой точке каждого слоя совпадают с направлениями координат 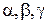, т.е. в каждой точке слоя одна из плоскостей упругой симметрии параллельна координатной поверхности оболочки, а остальные две перпендикулярны координатным линиям .

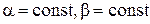Тогда для упругих постоянных 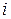-го слоя оболочки имеем

(2.44)

, , ,

, , .

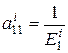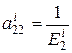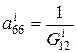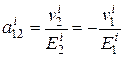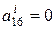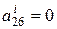Для коэффициентов 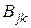из (2.19, 2.20) имеем

(2.45)

, ,

,

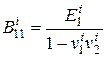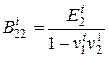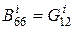
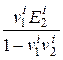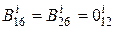
ля основных напряжений из (2.16 – 2.18) получим

,

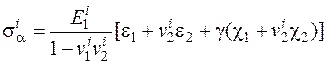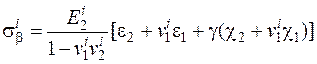, (2.46)

.

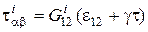Формулы для определения жесткостей (2.29) остаются без изменений, при этом значения 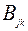надо принимать из условий, что

, , .

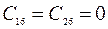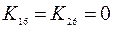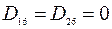Тогда получим следующие соотношения упругости

;

;

;

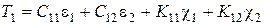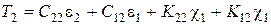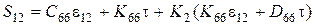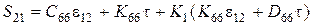; (2.47)

;

;

,

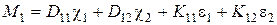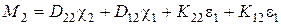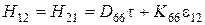и выражения для потенциальной энергии

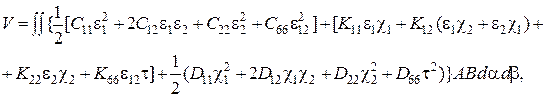(2.48)

Выражения деформаций и изменений кривизны, кручения, уравнения равновесия и неразрывности деформаций остаются без изменений.