Упорядоченные наборы с повторением и без повторений

1.1. Упорядоченные наборы а элементов n данных 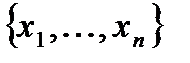с возможными повторениями.

Пример. Упорядоченные наборы3-х элементов множества {1,2} — это упорядоченные множества

{111} {112} {121} {122} {211} {212} {221} {222}. Упорядоченные наборы называют также словами.

Теорема. Число упорядоченных наборов с возможными повторениями а элементов из n данных есть n .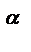

Доказательство. Пусть F 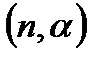есть искомое число упорядоченных набо­ров с повторениями 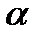элементов из n данных. Тогда разобьем все упорядоченные наборы на n групп, где в i-тую группу войдут те на­боры, которые начинаются на 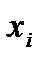-ый элемент. В нашем примере, где n= 2 , 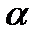= 3 группы выглядят так:

1: 111, 112, 121, 122;

2: 211, 212, 221, 222.

Тогда число наборов в каждой группе равно числу

упорядоченных наборов 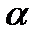-1 элементов из n данных, т. е. F 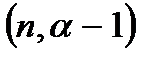, а число групп есть n. Поэтому

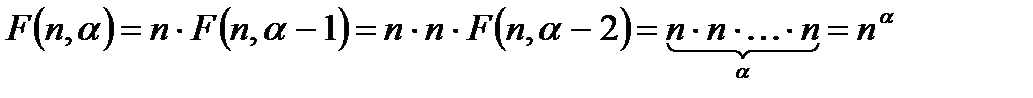
Пример 1. Дан алфавит из n букв 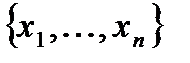. Найти число различных слов длины 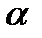в этом алфавите.

Решение. Нетрудно видеть, что это число равно числу упорядоченных

наборов 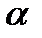элементов из n данных, т. е .

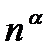Пример 2. Дано множество из n элементов 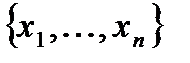. Найти число различных подмножеств этого множества.

Решение. Для каждого подмножества введем характери­стический вектор длины n, компонента i которого равна 1, если 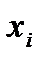входит в рассматриваемое подмножество, и 0 в про­тивном случае. Тогда характеристический вектор (слово в {0,1} длины n) однозначно определяет подмножество множества 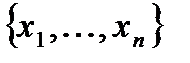. Поэтому число подмножеств равно .

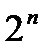Пример 3. Пусть дано V — множество 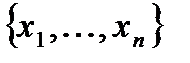и множество Р некоторых упорядоченных пар 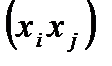. Тогда (V,P) называют ориентированным графом, V — множество вершин, Р — ориентированные ребра. Ребро 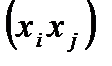называют петлей. Полным ориентированным графом с петлями на множе­стве V называют граф со всеми ориентированными ребрами. Тогдачислоребер в полном ориентированном графе равно .

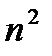Упорядоченные наборы 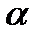элементов из n-данных

без повторения ( ).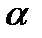

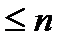Пример. 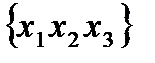, 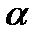= 2. Тогда упорядоченные наборы без повторения:

.

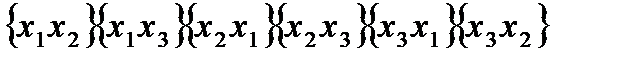Теорема. Число упорядоченных наборов 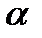элементов из n данных есть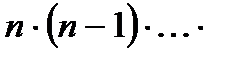

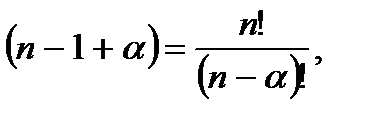
где 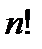есть произведение. . Обозначают это число .

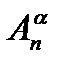Доказательство. Пусть 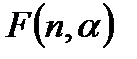есть искомое число упорядоченных наборов 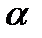элементов из n данных без повторения. Тогда разобьем все эти наборы на n групп, в i-тую группу войдут наборы, начинающиеся на 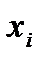. Тогда число элементов в i-ой группе равно числу упорядоченных наборов 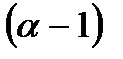- ого элемента из ( 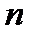— 1)-ого данного, так как элементы в наборе не повторяются, т.е. числу 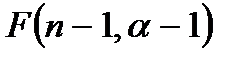. Поэтому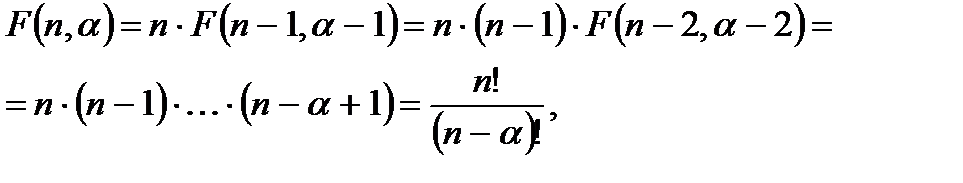

т.к.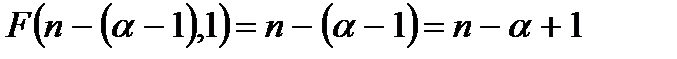

В нашем примере группы выглядят так:

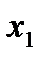
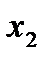
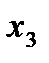
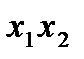
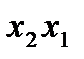
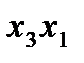
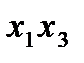
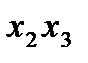
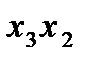
Упорядоченный набор n элементов из n данных без повторения называют перестановкой: 1,2,3. Перестановки

{123} {132} {213} {231} {312} {321} .

Число перестановок из n- элементов есть 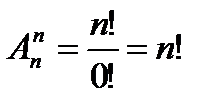(0! считаем равным 1).

Пример 1. Пусть (V, Р) — ориентированный граф. Полным

ориентированным графом называют граф, в котором присутствуют все

ориентиро­ванные ребра, кроме петель.

Тогда ориентированные ребра такого графа есть упорядоченные

пары из множества 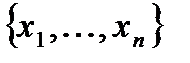без повторений, и их число по доказанной теореме есть

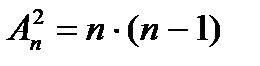
Пример 2. Имеется n мест и 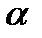человек. Скольким числом способов можно рассадить этих 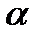человек на 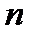местах.

Решение. 1. 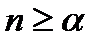. Занумеруем места числами 1,2, ... , 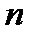. Тогда каждому упорядоченному набору 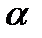элементов из 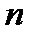соответствует способ посадки. Поэтому искомое число есть

.

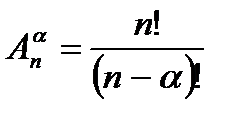2. Занумеруем людей 1,2,.. ,. 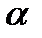. Тогда каждому упорядо­ченному выбору 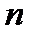элементов из 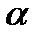данных соответствует способ посадки и наоборот. Поэтому искомое число есть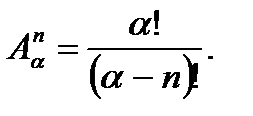

5.2 Неупорядоченные наборы 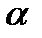элементов из 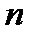данных без повторений.

Неупорядоченные наборы 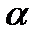элементовиз 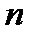данных без повторений будем просто называть набором. (Иногда называют сочетанием 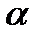элементов из 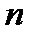данных).

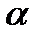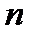Пример: {123} наборы двух элементов из 3: {12} {13} {23}. Наборы из данных это 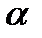-элементные подмножества 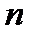-элементного

множества.

Теорема . Число 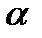-элементных наборов есть 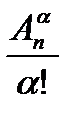Обозначают это чи­сло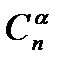

Доказательство. Рассмотрим все упорядоченные наборы 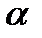элементов из 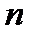без повторений и разобьем их на группы так, что в одну груп­пу попадают упорядоченные наборы, состоящие из одних элементов множества 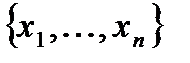, (т.е. в группе, в которой содержится упорядо­ченный набор 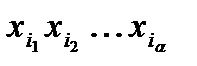, содержатся все перестановки элементов 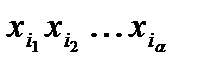), и поэтому число упорядоченных наборов в каждой

группе есть 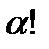.значит число групп есть 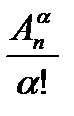, а это число групп и есть число 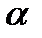-элементных подмножеств множества 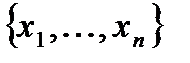и по­этому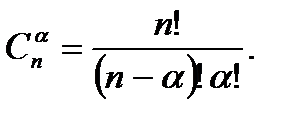

Пример 1. Каким числом способов можно создать группу из 10 человек

на курсе из 100 человек.

Решение. Очевидно, что искомое число есть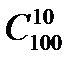

Пример 2. Бином Ньютона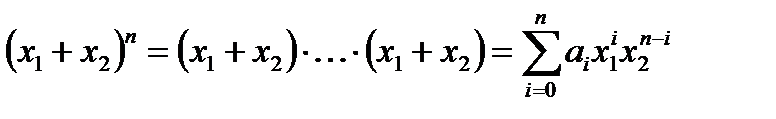

Коэффициент 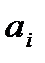, равен числу наборов i элементов из п данных ( числу вы­боров i скобок из n данных, в которых для образования слагаемого 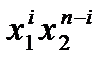брали 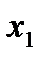, а в невыбранных скобках брали 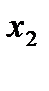), и поэтому =

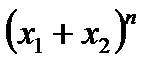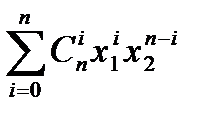
Как частный случай получим очевидное равенство .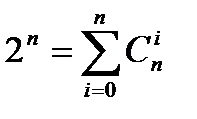

Пример 3. Графом без петель называют множество вершин V= 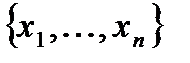и множество некоторых пар вершин Е: 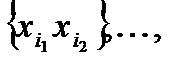называе­мых ребрами, здесь петлей называют пару 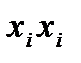, (и таких пар в Е нет). Полным графом на множестве вершин V= 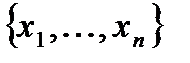называют граф со всеми ребрами, т.е. Е есть все пары из множества 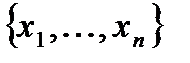кроме петель.

Из теоремы следует, что число ребер в полном графе есть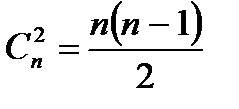

5.3 Неупорядоченные наборы 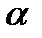элементов из п данных 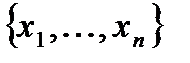с возможными повторениями.

Пример. {1,2,3}, 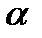= 2 наборы:

{(12)(13)(23)(11)(22)(33)}.

Теорема. Число неупорядоченных наборов ос элементов из п данных с возможными повторениями есть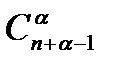

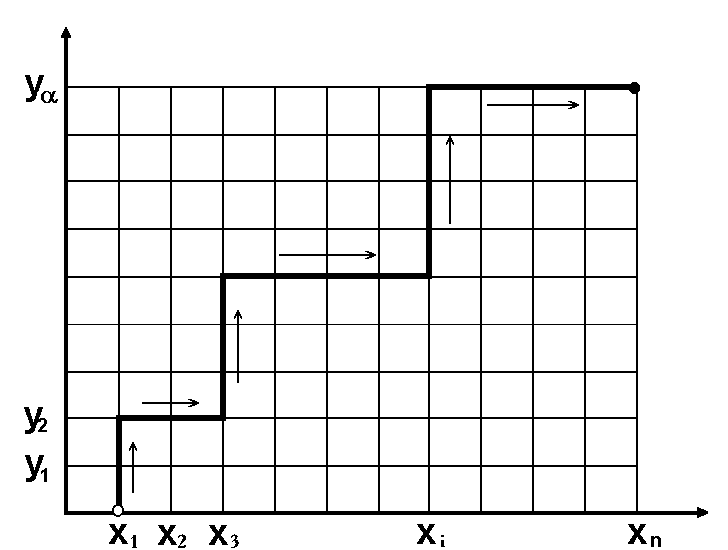
Доказательство. Рассмотрим таблицу на декартовой системе координат и рассмотрим пути из точки 0( 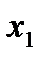, 0) в точку ( 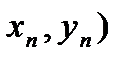, причем каждый раз мы можем сдвигаться либо вверх, либо вправо. Тогда в каждом пути имеется п — 1 точка, из которой мы двигались вправо, и 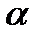точек из которых мы двигались вверх, поэтому общее число точек на пути 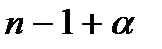, и каждый путь определяется выбо­ром 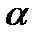точек, по которым проходило движение вверх. Поэтому число всех путей есть 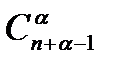. Нетрудно установить взаимно однозначное соответствие между неупорядоченными наборами 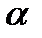элементов из 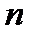данных с повторениями и всеми возможными путями. Так указан­ному пути соответствует набор 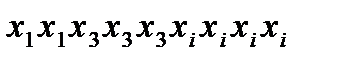, (т.е. элемент 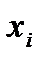, выбираем столько раз, сколько происходило движений вверх на нем).

Поэтому число неупорядоченных наборов 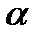элементов из 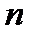данных с возможными повторениями есть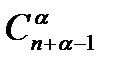

Пример 1. Рассмотрим уравнение в целых неотрицательных числах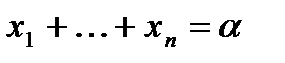

Сколько различных решений оно имеет?

Решение. Каждому решению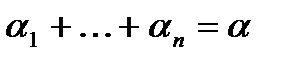

поставим в соответствие 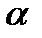-элементный набор неупорядоченный 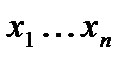, где 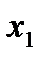выбирается 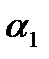раз, ... , 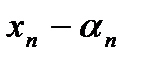раз. Это соответствие взаимно однозначно. Тогда искомое число есть .

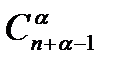Пример 2. Имеется 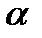одинаковых шаров и 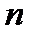различных урн. Сколько различных способов разложить шары в урны.

Решение. Каждому разложению соответствует выбор первой урны 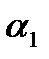раз, второй урны 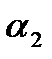раз, ... , 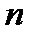-ой урны 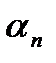раз, так что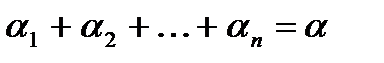

Поэтому искомое число есть .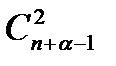

Упражнения.

1. На ж/д. станции имеется т светофоров. Сколько может быть дано раз­личных сигналов, если каждый светофор имеет три состояния: красный, желтый и зеленый?

2. Сколько существует матриц размера т, п, элементы которых прини­мают значения 0 или 1 ?

3. Какое число позиций из трех различных фигур существует на шах­матной доске 8х8?

4. Имеется шесть претендентов на три вакантные должности. Какое чи­сло возможных назначений имеется?

5. Имеется семь различных автобусов. Каким числом способов можно выбрать три из них на три различных маршрута?

6. Десять человек голосуют за трех кандидатов. Можно голосовать толь­ко за одного кандидата. Какое число возможных результатов выборов?

7. Подкидывают пять различных игральных костей. Какое возможное число исходов?

8. Какое число расстановок восьми одинаковых ладей имеется, чтобы никакая пара ладей не угрожала друг другу?

9. Какое число способов составить расписание из пяти предметов на один день имеется?

10. Найти число различных конъюнкций на множестве n переменных.

11. Найти число двоичных наборов длины n с k единицами.

12. Имеется колода из 36 карт, выбирают 3 карты. Какое число возмож­ных выборов имеется?

13. Имеется 10 предметов. Каким числом способов можно составить набор из трех предметов?

14. Бросают пять одинаковых игральных костей. Найти возможное число исходов.

15. Имеется три одинаковые колоды по 36 карт в каждой колоде. Найти число возможных выборов трех карт.

16. Сколькими способами можно посадить за круглый стол 5 муж. и 5 жен. так чтобы никакие два лица одного пола не сидели рядом.

17. Сколькими способами можно посадить на карусель 5 муж. и 5 жен. Так, чтобы никакие два лица одного пола не сидели рядом, и способы, переходящие друг в друга при вращении карусели считать совпадающими.

18. Из колоды содержащей 52 карты вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз?

19. Из колоды содержащей 52 карты вынули 10 карт. Во скольких случаях среди этих карт окажется ровно один туз?

20. Из колоды содержащей 52 карты вынули 10 карт. Во скольких случаях среди этих карт окажется не менее двух тузов?

21. В некотором государстве не было двух жителей с одинаковым набором зубов. Какова может быть наибольшая численность населения?

22. У мамы 2 яблока и три груши. Каждый день в течение 5 дней она выдает по одному фрукту. Сколькими способами это может быть сделано?

23. У мамы m яблок и n груш. Каждый день в течении m дней подряд она выдает по 1 фрукту. Сколькими способами это может быть сделано?

24. У мамы 2 яблока,3 груши и 4 апельсина. Каждый день в течение 9 дней она выдает по одному фрукту. Сколькими способами это может быть сделано?

25. У отца есть пять попарно различных апельсинов, которые он выдает своим 8 детям так, что каждый получает либо один апельсин, либо ничего. Сколькими способами это можно сделать?

26. Сколькими способами можно надеть пять различных колец на пальцы одной руки, исключая большой палец?

27. 30 человек голосуют по пяти предложениям. Сколькими способами могут распределиться голоса, если каждый голосует за одно предложение и учитывается лишь число голосов, поданных за каждое предложение?

28. 30 человек голосуют по пяти предложениям. Сколькими способами могут распределиться голоса, если каждый голосует за одно предложение?

29. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?

30. Сколькими способами можно составить 6 слов из 32 букв, если в совокупности этих 6 слов каждая буква используется один и только один раз?

31. Сколькими способами можно выбрать 12 человек из 17, если данные двое не могут быть выбраны вместе?

32. Сколько имеется 6-ти значных чисел, у которых три цифры четные, а три нечетные?

33. Найти сумму четырехзначных чисел, получаемых при всевозможных перестановках цифр 1,2,3,4.

34. Найти сумму четырехзначных чисел, получаемых при всевозможных перестановках цифр 1,2,2,5.

35. Найти сумму четырехзначных чисел, получаемых при всевозможных перестановках цифр 1,3,3,3.

36. Найти сумму четырехзначных чисел, получаемых при всевозможных перестановках цифр 1,1,4,4.

37. Сколько нечетных чисел можно составить из цифр числа 3694 (каждую цифру можно использовать не более одного раза).

38. Сколькими способами можно переставить цифры числа 12 341 234 так, чтобы никакие две одинаковые цифры не шли друг за другом?

39. Сколькими способами можно переставить цифры числа 12 345 254 так, чтобы никакие две одинаковые цифры не шли друг за другом?

40. Стороны каждой из двух игральных костей помечены числами 0,1,3,7,15,31. Сколько различных сумм может получиться при метании этих костей?

41. Стороны каждой из трех игральных костей помечены числами 1,4,13,40,121,364. Сколько различных сумм может получиться при метании этих костей?

42. Хор состоит из 10 участников. Сколькими способами можно в течение трех дне выбирать по 6 участников, так, чтобы каждый день были различные составы хора?

43. Сколько и каких цифр понадобиться, чтобы записать все натуральные числа, меньшие 10?

44. Сколькими способами из 28 костей домино можно выбрать две кости так, чтобы их можно было приложить друг к другу (т. е. некоторое число очков встретилось на обеих костях).

45. Город имеет вид прямоугольника, разделенного улицами на квадраты. Таких квадратов в направлении с севера на юг n, а с востока на запад k.. Сколько имеется кратчайших дорог от одной из вершин прямоугольника до противоположной?

46. Сколькими способами можно расставить k ладей на “шахматной” доске размером n 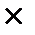n так, чтобы они не угрожали друг другу, т.е. так, чтобы никакие две из них не стояли на одной вертикали или горизонтали? Рассмотреть случай k=n и имеется p белых и k-p черных ладей.

Разное.

В следующих пяти задачах следует посчитать число возможных комби­наций, получающихся при бросании пяти различных (одинаковых) играль­ных кубиков.

1. Комбинации 3+2, т.е. на некоторых двух и оставшихся трех костях одинаковые цифры. Пример:11144 или 33333

2. Комбинации: имеется хотя бы четыре одинаковые цифры. 44443 или 44444.

3. Комбинации: 2+2, то есть на некоторых двух парах костей одна цифра. 11224 или 11222 или 11113 или 11111.

4. Комбинации: на всех костях различные цифры 134.56

5. Комбинации, когда хотя бы на трех костях одна цифра. 11123 или 11114 или 11111.

6. Имеется колода карт 4-рех мастей по 9 карт каждой масти. Из выборов 7-ми карт найти число комбинаций, когда имеются все масти.

7. Составляют шестизначные числа из цифр 1,2,3. Найти число чисел, в которых участвуют все цифры. - .-

8. Найти число шестизначных чисел из цифр 1,2,3 с четной суммой цифр. Все цифры присутствуют в числе.

9. Найти число вершин, ребер, граней, кубов четырехмерного булевого куба.

10. Найти число счастливых четырехзначных номеров с суммой цифр не больше 18.

11. Найти ошибку в решении следующей задачи:

Имеется колода карт4-ех мастей по 9-ть карт каждой масти. Берут шесть карт. Найти число комбинаций, в которых имеются все масти, причем, в некоторые две масти попало по две карты в каждую, а в оставшиеся масти по одной.

Решение. Выбираем первую масть и две карты, которые попали в эту масть: имеем 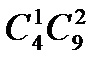способов. Затем выбираем еще одну масть и две карты в ней таким же числом 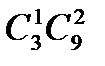способов. После этого в оставших­ся двух мастях выбираем по одной карте: 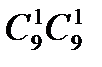возможностей. Теперь перемножаем все числа и получаем ответ: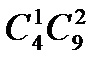 .
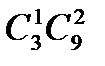
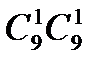