Классификация задач по степени сложности

В предыдущей главе мы убедились, что для решения задачи об эйлеровом цикле имеется прекрасный линейный алгоритм – его сложность O(m), т.е. он линейно зависит от числа ребер. В следующей главе мы рассмотрим задачу, очень похожую на задачу Эйлера. Она состоит в поиске цикла, проходящего через каждую вершину графа только один раз. Эту задачу изучал Гамильтон, и в честь него она получила название задачи Гамильтона (рис. 9.1).

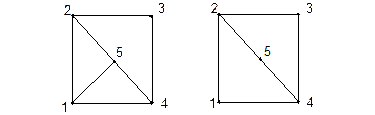
В этом графе существует гамильтонов цикл

В этом графе гамильтонова цикла нет

Рис. 9.1. Задача Гамильтона

Многие математики в течение нескольких веков занимались задачей Гамильтона. До сих пор неизвестно ни одного простого необходимого и достаточного условия существования гамильтонова цикла, и до сих пор не построен алгоритм, который проверял бы существование гамильтонова цикла в произвольном графе за полиномиальное число шагов (число, ограниченное многочленом фиксированной степени от числа вершин графа).

В следующей главе мы рассмотрим экспоненциальный алгоритм для нахождения гамильтонова цикла (всех гамильтоновых циклов). Сейчас нас интересует то, что мы столкнулись с задачей другой степени сложности.

Основное различие между математикой и информатикой заключается в том, что в информатике недостаточно иметь доказательство существования объекта, недостаточно найти конструктивное доказательство этого факта, т.е. алгоритм. Мы должны учитывать противоречия пространства и времени, которые навязывает нам мир: необходимо, чтобы решение можно было вычислить, используя объем памяти и время, приемлемое для человека или машины.

Идеальный случай, когда для решения задачи известна явная математическая формула. Тогда сложность задачи не зависит от входных данных и является постоянной.

Если же мы не располагаем ни явной формулой, ни рекурсивным выражением приемлемой сложности, нам остается только два способа:

ü построение эффективного алгоритма;

ü метод перебора всех возможностей.

Сложность задачи – сложность наилучшего алгоритма, известного для ее решения.

Сложность алгоритма – число шагов, необходимых для решения наихудшего из всех возможных случаев, допускающих применение алгоритма.

Это число выражается как функция от размерности входных данных задачи – например, числа вершин графа.

Сразу возникает вопрос – если сложность задачи зависит от нашего знания «хороших» алгоритмов, до какого предела можно улучшать данный алгоритм?

Существуют ли методы перевода задачи из класса «сложных» в класс «простых»?

ТРИ КЛАССА ЗАДАЧ

Самыми лучшими являются линейные алгоритмы порядка O(n), где n – размерность входных данных, например алгоритм поиска эйлеровых циклов в графе. Другие «хорошие» алгоритмы имеют сложность, представляющую собой многочлен заданной степени, не зависящей от входных данных: О(nm), O(n²), O(n³) и т.д. Задачи, решаемые алгоритмами полиномиальной вычислительной сложности, относятся к классу Р полиномиальных алгоритмов.

Есть задачи, которые по своей природе имеют экспоненциальную сложность порядка Aⁿ, где A – константа или полином от n. Это задачи, в которых требуется построить все подмножества данного множества, все клики (полные подграфы) данного графа и т.д. Число ответов в этих задачах уже само по себе экспоненциально, поэтому только их перечисление потребует экспоненциальное число шагов. Это класс Е экспоненциальных алгоритмов.

Остаются задачи, не попавшие ни в класс Р, ни в класс Е. В их условиях не содержатся экспоненциальные множества, для них не разработан полиномиальный алгоритм, но и не доказано, что такого алгоритма не существует.

Вот неполный список таких задач. (В приложении содержатся точные математические постановки 32 различных задач.)

ü Решение систем уравнений в целых числах.

ü Определение гамильтонова цикла.

ü Составление расписаний и раскрасок.

ü Существование множества значений логических переменных, которые позволяют сделать значение произвольного заданного логического выражения истинным.

ü Оптимизация пути коммивояжера через сеть городов.

ü Отбор файлов при запросе в информационный банк данных для получения информации с наименьшей стоимостью.

ü Размещение обслуживающих центров для максимального числа клиентов при минимальном числе центров.

ü Оптимальная загрузка емкости, оптимальный раскрой.

ü Диагностика (болезни, поломки).

Этот список далеко не полон, так как большая часть современных задач относится к этому классу. Кроме того, названные задачи являются модельными. Каждой из них соответствует несколько реальных формулировок:

ü упорядочение операций;

ü размещение персонала;

ü оптимизация перевозок;

ü управление производством;

ü проектирование в области электроники.

Более того, для большинства этих задач (так называемых
NP–полных задач) была доказана эквивалентность – если для одной из них удастся найти полиномиальный алгоритм, автоматически будут решены все остальные.

Назовем его классом NP недетерминированных полиномиальных алгоритмов. К сожалению, детальное обсуждение этих задач выходит за рамки данной главы, но при практическом изучении подобных задач нужно помнить следующее:

1. Для небольших n экспоненциальный алгоритм часто более эффективен, чем полиномиальный.

2. Для реальных задач большой размерности следует разработать приближенный полиномиальный алгоритм.

Алгоритмы с возвратом

Вернемся к задаче существования гамильтонова пути– пути, проходящего через каждую вершину графа только один раз. В предыдущей главе было упомянуто, что для такой задачи не построен полиномиальный алгоритм. Попробуем произвести полный перебор всех возможных путей. N вершин графа можно расположить в n! различных цепочек. Чтобы проверить для каждой цепочки, реализована ли она как гамильтонов путь на графе, необходимо еще n шагов, итого сложность полного перебора nn! шагов.

Такая величина растет гораздо быстрее экспоненты, поэтому полный перебор является неприменимым методом. Однако число шагов в алгоритмах переборного типа можно значительно уменьшить.