Математическая зимушка

– Прозвенел уже школьный звонок,

Он позвал нас всех на урок.

Будьте все внимательны,

А ещё старательны.

Будем сегодня задачи решать,

Будем складывать и вычитать.

Мы будем готовиться к контрольной работе, которая ждёт нас на этой неделе.

Разминка:

1. Наступил декабрь, на землю упали 3 шишки, а потом ещё 2. Сколько всего шишек упало на землю?

2. Дети лепили снеговика. После прогулки на батарее сохло 14 мокрых варежек. Сколько детей лепило снеговика?

Задание 1:

1. Самое маленькое двузначное число.

2. Самое большое двузначное число.

3. На сколько одно больше другого?

4. Назовите все двузначные числа, число единиц в которых равно 5.

5. Назовите все двузначные числа, число десятков в которых равно 5.

Задание 2:

– Вставьте пропущенные единицы, так чтобы равенства стали верными

1…= 10

1…= 60

1…= 90

Задание 3:

– Замените словесную запись числовым выражением (на доске):

Задание 4:

– Самостоятельная работа по вариантам.

1. 54+20 70-5 60+18 43-2

2. 20+14 60-8 46+30 88-7

Задание 5:

– У нас сегодня в гостях сказочный герой. Что это за звуки? Кто это? У Карлсона для вас конверт с заданиями. Это задачи.

1. Фрекен Бок испекла 10 ватрушек, а плюшек на 4 больше. Сколько плюшек испекла Фрекен Бок? Кто может записать краткое условие задачи? Выберите верное выражение:

10+4

10-4

10+ (10+4)

(10+4) -10

– Почему именно это? Давайте запишем в тетрадь решение этой задачи. Как нужно изменить вопрос, чтобы задача решалась выражением 10+(10+4)? Сколько получится?

2. В коробке было 13 конфет. Малыш успел съесть 5 конфет, остальные конфеты съел Карлсон. Кто может решить эту задачу? Правильно, это не задача. Здесь не хватает вопроса. Какой вопрос можно поставить? Сделаем чертёж к задаче.

Задание 6:

– Ребята, мы с вами знаем, что Карлсон большой сладкоежка. А если бы у вас было 13 конфет, как бы вы поделили их со своим другом или подругой.

Задание 7:

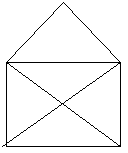
– Карлсон полетел к себе в домик на крыше. Он выглядит вот-так. Сколько здесь треугольников?

– Карлсон улетел, а Малыш остался делать уроки. Ему задали расшифровать очень сложный пример. Давайте поможем Малышу.

1А+ 2А+3А=7А

– Малыш благодарит вас за помощь.

Подведение итогов:

– Вам понравился сегодняшний урок? Давайте вспомним, какие задания мы выполняли. Какое задание вам особенно понравилось? Какое было самым трудным? Самым легким?

Карлсон и Малыш передали для вас подарки - это раскраски. Дежурные раздают.

ГЛАВА 2. ДИДАКТИЧЕСКИЕ ИГРЫ, РАСЧИТАНЫЕ НА ЭТАП УРОКА

Математические игры

«Назови соседей»

Играющие ученики садятся в кружок. Ведущий бросает мяч ребенку, называя числа от 0 до 30. Поймавший мяч должен назвать «соседей» данного числа, т.е. числа на один меньше и на 1 больше названного, или предыдущее и последующее.

После этого он возвращает мяч ведущему. Если поймавший мяч ребёнок дважды ошибается в названии «соседей», он выбывает из круга и внимательно следит за игрой со стороны.

«Быстро занять места!»

Учащиеся разбегаются по всей площадке, собирают на полу жетончики с номерами. Учитель произносит команду: «Быстро занять места!». Дети спешат занять свои места, согласно тем цифрам, которые имеются на их жетонах, по порядку.

«Эхо»

Школьники идут в колонне по одному. Учитель называет число, а дети как эхо, повторяют его и последующее (повторяют его и предыдущее).

«Кто ушел?»

Ученики строятся в круг. Водящий встает в центр круга, запоминает, какие цифры на карточках в руках у детей (только четные; только нечетные; по возрастанию; по убыванию и т.д.) закрывает глаза. Учитель дотрагивается до одного из играющих, стоящих в круге, и он тихо выходит из зала. Учитель спрашивает у водящего: «Отгадай, кто ушел?» (какой цифры не хватает). Если водящий отгадал, то он встает в круг и выбирает другого водящего. Если не отгадал, то снова закрывает глаза, а выходивший из зала занимает своё прежнее место в кругу. Водящий, открыв глаза, должен назвать его.

«Знают все свои места!»

Учащиеся строятся на площадке в шеренгу. Каждый получает карточку с примером типа: 5 – 2; 8 + 2; 3 + 4.… С результатом от 0 до 10. по сигналу или по команде учителя «Разойдись!» дети расходятся по площадке и дружно говорят:

У ребят порядок строгий,

Знают все свои места.

Ну, трубите веселее:

Тра-та-та, тра-та-та.

За это время учитель на площадке в разных местах крепит карточки с цифрами от 0 до 10.

После сигнала учителя дети быстро занимают свои места, согласно решенному примеру.

«Передай кубик»

На первую парту каждого ряда ставится пластмассовый цветной кубик.

По сигналу учителя кубик передается каждому ученику по очереди, с названием чисел по порядку, пока не возвратится обратно на первую парту. Затем точно так же передают кубик с названием чисел по убыванию, называя каждое предыдущее число.

Ряд, закончивший передачу кубика первым, побеждает.

Игра повторяется 2-3 раза.

«Микрокалькулятор»

Мы устали от сложения

И тетрадки спрятали,

Дайте нам для ускорения

Микрокалькуляторы.

Дети делятся на две команды. Игроки решить пример на карточке, пробежать эстафету и взять в конце пути в корзине столько предметов, какой ответ получился при решении примера на карточке. Например, 3 – 2 = 1, значит, игрок берет 1 предмет.

Примеры на карточках:

Команда 1 Команда 2

5 – 3 8 + 2

6 – 4 10 – 3

8 – 1 7 + 2

3 + 4 8 – 6

7 + 3 9 – 7

У каждой команды должно получиться в конце эстафеты по 30 предметов.

«Парная игра»

Ученикам раздают плоскостные геометрические фигуры и контуры этих фигур. Дети, держа в руках фигуры, выстраиваются в шеренгу. По команде учителя они ищут себе пару согласно своей фигуре (плоскостная должна соединиться с контурной).

«Зрительный диктант»

Ученикам предлагается посмотреть на наборное полотно, где слева направо расставлены 3 – 5 геометрических фигур. Две команды под музыкальное сопровождение 1 – 2 минуты, должны расставить на площадке в такой же последовательности, как в образце, геометрические фигуры более крупного размера и назвать их.

Выигрывает та команда, которая быстро и без ошибок справляется с заданием.

«Построение в шеренгу»

Ученики строятся в шеренгу по росту. Учитель дает им следующие задания:

- Кто в классе самый высокий?

- Какой по росту Саша? (Саша самый низкий.)

- Кто твой сосед слева? Справа?

- Между кем и кем ты стоишь?

- Шаг вперед сделает Маша.

- Таня, сделай шаг влево.

- Сзади Тани встанет Аня, а впереди Сережа.

«Живые числа»

Ученики получают таблички с числами. Каждый крепит свою табличку на грудь. Учитель дает команду: «Числа, встаньте по порядку!». Участники игры становятся в шеренгу, лицом к классу и пересчитываются от 1 до 10 и обратно от 10 до 1.

«Белочка и грибы»

Кто по елкам ловко скачет?

И взлетает на дубы?

Кто в дупле орешки прячет,

Сушит на зиму грибы?

Учитель рассказывает учащимся о том, что белочка на зиму делает запасы грибов. В одном дупле белочка никогда не хранит запасы, а раскладывает в 2 – 3 дупла. Белочка каждый день сушила по 7 белых грибов (число можно менять) и раскладывала их в два дупла. По сколько грибов в каждое дупло может положить белочка? Дети выходят к доске и раскладывают грибы в «дупла».

«Кто быстрее нарядит ёлочку?»

Вывешиваются два плаката с изображением ёлочек. На доске записаны столбики примеров, по 8 – 10 в каждом. К доске выходят два ученика. У каждого из них по 8 – 10 картонных игрушек с крючками. По сигналу учителя дети начинают решать примеры. Решив пример, учение вешает игрушку на свою елочку.

«Строим дом»

Мы построили просторный

Четырехэтажный дом,

И для всех своих игрушек

Место в доме мы найдем.

В доме окна есть и двери,

Крыша крашеная есть…

Здесь поселятся игрушки.

Хорошо им будет здесь!

После прочтения стихотворения учитель говорит:

Сегодня будем строить дом

На радость новоселам,

Чтоб каждый становился в нем

Счастливым и веселым!

После этих слов из различных геометрических фигур, учащиеся на партах, у доски строят дом. Затем называют геометрические фигуры, отвечают на вопросы: Сколько? Каких фигур больше?

«У кого больше фигур?»

У каждого ученика на парте лежат небольшие фигуры (круги, треугольники, квадраты).

Назначают пять водящих. По сигналу учителя они расходятся по классу и подходят к любому сидящему за партой. Тот ученик, к кому подошли, говорит пример на табличное умножение или деление. Водящий тихо, чтобы никто не слышал его ответ, называет результат. Если ответ верный, он получает фигуру. Тот, кто за определённое время наберёт больше фигур, считается победителем. Возможен и обратный вариант игры.

«Мальчики – девочки»

Учитель берёт одну из карточек, показывает пример классу и переворачивает карточку обратной стороной. Если карточка красного цвета, то ответ хором называют девочки, если синего – мальчики. Выигрывает тот, кто допустит меньше ошибок.

«Не скажу»

Учащиеся считают от 1 до 40 по одному. Вместо чисел, которые, например делятся на 2, они говорят "Не скажу!” В игре происходит целенаправленное формирование механизма произвольного переключения внимания.

«Кто быстрее, кто вернее»

Учитель раздаёт на каждый ряд по одному комплекту цифр от 1 до 9 так, что каждому ученику достаётся какая-то одна цифра. Учитель читает примеры вслух (4 * 4, 9 * 2 и т.д.). Учащиеся должны быстро сообразить, сколько получится, выйти к доске, если нужная для ответа цифра у него, и составить число-ответ.

За каждый верно показанный ответ начисляется одно очко, если ряд успел первым показать его. Ряд, набравший большее количество очков, выигрывает.

«Живая математика»

У учащихся на груди таблички с цифрами от 0 до 9. Учитель читает примеры. Встаёт ученик, у которого есть цифра-ответ. Лучше давать примеры на деление, чтобы получались однозначные цифры. В случае двузначного ответа должны встать два ученика. Проводить игру желательно в конце урока для повышения двигательной активности учащихся. Также можно раздавать по несколько одинаковых цифр, привлекая большее количество детей.

Старинные задачи

Ещё в древней Руси люди решали разные задачи. Например в XIX веке в деревнях загадывали:

1. «Шли семь старцев.

У каждого старца по семи костылей.

На каждом костыле по семи сучков.

На каждом сучке по семи кошелей.

В каждой кошеле по семи пирогов.

В каждом пироге по семи воробьев.

Сколько всего?»

2. Как записать число 100 шестью цифрами 4?

3. Как записать число 100 семью цифрами 4?

4. Как записать число 1000 пятнадцатью цифрами 4?

5. Летела стая гусей , а навстречу ему ещё гусь. Гусь говорит: « Здравствуйте, сто гусей». А ему отвечают : «Нас не сто гусей, а меньше. Если бы нас было столько, да ещё полстолька, да ещё четверть столько, да ты, гусь, вот тогда было бы нас сто гусей» . Сколько гусей было бы в стае?

6. Семь старух отправились в Рим. У каждой старухи по семи ослов, каждый осел несёт по семи мешков, в каждом мешке по семи хлебов, в каждом хлебе по семи ножей, каждый нож в семи ножнах. Сколько всего предметов?

7. Имеет 4 зуба. Каждый день появляется за столом, а ничего не ест. Что это?

8. На какое дерево садится ворона во время проливного дождя?

9. У бабушки Даши внучка Маша, кот Пушок, собака Дружок. Сколько у бабушки внуков?

10. Сколько горошин может войти в обыкновенный стакан?

11. На четырёх ногах стою, ходить же вовсе не могу.

12. Может ли дождь идти два дня подряд?

13. Двенадцать братьев друг за другом стоят, но друг друга не видят.

14.Первый Назар шёл на базар,

Второй Назар с базара.

Какой Назар купил товар,

Какой шёл без товара?

15. Какой знак надо поставить между написанным рядом цифрами 2 и 3, так чтобы получилось число, больше двух, но меньшее трёх?

16. Половина – треть его. Какое это число?

17. Когда моему отцу был 31год, мне было 8 лет, а теперь отец старше меня вдвое. Сколько мне лет теперь?

18. За книгу заплатили 1 рубль и ещё половину стоимости книги. Сколько стоит книга?

19. У одного папы спросили : « Сколько у вас детей?» Он ответил: « У меня четыре сына и у каждого из них есть родная сестра.» Сколько же у него детей?

20. Летела стая гусей . 1 гусь впереди, 2 позади, 1 гусь между двумя и 3 в ряду. Сколько всего гусей.

21. Шли две матери с дочерьми, да бабушка с внучкой. Нашли полтора пирога. По сколько им достанется?

22. Меня зовут Толей. У моей сестры только один брат, как зовут брата моей сестры?

23. По улице идут два отца и два сына. Всего три человека. Может ли быть такое?

24. Шёл Кондрат в Ленинград, а навстречу ему семь ребят. Сколько ребят шли в Ленинград?

Занимательные задачи

1. Шесть пирожных разделили между братьями и сестрами так, что у братьев их оказалось на два меньше, чем у сестер. Сколько у кого?

Решение. Задача может быть решена угадыванием. Однако желательно дать и решение с вопросами. Этого можно добиться, если нарисовать два отрезка, один из которых на две клетки больше другого. Как узнать, сколько клеток должно быть в каждом отрезке? Сумма этих трех отрезков должна равняться 6 клеткам. Значит, сумма двух равных отрезков равна 6 – 2 = 4, а каждый из них 2. Когда учащимся покажется, что это рассуждение ими понято, нужно записать его по вопросам и действиям. Нужно подсказать первый вопрос:

1) Сколько было бы пирожных, если бы у сестер было столько же, сколько у братьев? 6 – 2 = 4.

2) Сколько было пирожных у братьев? 4 : 2 = 2.

3) Сколько было пирожных у сестер? 2 + 2 = 4 (или 6 –2 = 4).

Ответ: у братьев 2, у сестер 4.

2. Ваня живет в 12-этажном доме, на 9 этаже, если считать сверху. На каком этаже живет Ваня?

Решение. Можно нарисовать дом, а можно решить задачу и без рисунка, узнав, сколько этажей дома находится ниже Вани (12 – 9 = 3).

Ответ: На 4 этаже.

3. В коробке лежит 15 шариков: черных, белых и красных. Красных шариков в 7 раз больше, чем белых. Сколько в коробке черных шариков?

Решение. Белых шариков не может быть больше одного, так как если бы их было хотя бы 2, то красных шариков было бы не меньше 14, а шариков всего 15. Значит, белый шарик всего один, а красных в семь раз больше, то есть семь. Черных шариков 15 – (1 + 7) = 7.

4. Пес Тузик на 6 кг тяжелее кота Барсика, а Барсик втрое легче Тузика. Сколько весит Барсик?

Решение можно сопроводить рисунком. 6 : 2 = 3 (кг) – вес Барсика.

Ответ: 3 кг.

5. Расшифруй предложение, в котором каждая буква заменена ее номером в русском алфавите и все слова написаны слитно:

(15)1(14)(17)6(19)(15)(33)(19)(20)(18)(16)(10)(20)(30)

(10)8(10)(20)(30)(17)(16)(14)(16)4(1)6(20).

Ответ: Нам песня строить и жить помогает.

6. Придумай возможное продолжение этой последовательности чисел: 1, 1, 2, 3, 5,…

Решение. 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5. Одно из правил, по которому может быть составлена эта последовательность, таково: первые два числа – единицы, а каждое число, начиная с третьего, равно сумме двух предыдущих чисел.

Ответ: Возможно такое продолжение: 8, 13, 21, …

7. У Васи и Коли вместе 15 марок. Вася подарил из них Коле 2 марки. Сколько стало у них вместе марок после этого?

Это – задача-шутка. Марок осталось, сколько было, – 15.

8. Какой вес можно взвесить гирями 1 кг, 2 кг и 4 кг на чашечных весах, если гири можно класть на одну чашу весов?

Решение можно сопроводить рисунками.

Ответ: Любой вес от 1 до 7 кг.

9. В коробке лежит 4 шарика: черных, белых и красных. Красных шариков столько же, сколько белых и черных вместе. Сколько черных шариков в коробке?

Решение. Красные шарики составляют половину всех шариков, то есть их 2. Черных и белых шариков вместе 2. Значит, их по одному каждого цвета.

Ответ: Черных 1, белых 1, красных 2.

10. У котенка на лапе 5 когтей, а у цыпленка 4. Во дворе находятся 10 котят и цыплят, а когтей у всех у них 104. Сколько котят во дворе?

Решение.

1) Сколько когтей у одного котенка? 5 х 4 = 20 (к.).

2) Сколько когтей у одного цыпленка? 4 х 2 = 8 (к.).

3) Сколько было бы когтей, если бы во дворе было 10 цыплят? 8 х 10 = 80 (к.).

4) Сколько когтей "лишние"? 104 – 80 = 24 (к.).

5) На сколько когтей у одного котенка больше, чем у одного цыпленка? 20 – 8 = 12 (к.).

6) Сколько было котят? 24 : 12 = 2 (кот.).

Ответ: 2 котенка.

11. У Даши и Маши 15 книг со стихами. Даше подарили еще три книги со стихами. Сколько теперь стало у них книг вместе?

Решение. Хотя мы не знаем, сколько книг было у Даши и сколько у нее стало книг, мы можем решить задачу. Если к одному из слагаемых прибавить некоторое число, то сумма увеличится на это число: (а + c) + b = (a + b) + c по сочетательному свойству сложения. Значит, от прибавления к книгам Даши еще 3 книг общее число книг увеличится на 3 книги, то есть станет равным 15 + 3 = 18.

Ответ: 18 книг.

12. Слава задумал число, прибавил к нему 1, отнял 2, умножил результат на 3 и разделил на 4. Получилось 6. Какое число задумал Слава?

Решение надо вести с конца: 6 х 4 : 3 + 2 – 1 = 9.

Проверка: (9 + 1 – 2) х 3 : 4 = 6.

Ответ: 9.

13. На двух полках стояло 19 книг. На каждую полку поставили еще столько книг, сколько было на ней. Сколько книг стало на двух полках после этого?

Решение. Если каждое слагаемое умножить на одно и то же число, то сумма умножится на это число: а х с + b х c = (a + b) х c. Так как сумма равнялась 19, а каждое слагаемое увеличили в 2 раза, то сумма увеличилась в два раза и стала равна 19 х 2 = 38.

Ответ: 38 книг.

14. Сколько существует двузначных чисел, у которых все цифры нечетные?

Решение. В двузначном числе две цифры. Первая цифра должна быть нечетной, то есть это может быть 1, 3, 5, 7 или 9. Вторая цифра также нечетная, то есть тоже 1, 3, 5, 7 или 9. Поэтому всего таких чисел 25. Это хорошо видно из таблицы:

Ответ: 25 чисел.

15. Проживание за один день в сказочной гостинице стоит 1 сольдо. У Буратино имеются купюры в 1 сольдо и в 2 сольдо. Как он должен расплачиваться ежедневно за гостиницу на протяжении 3 дней?

Решение желательно театрализовать. Пусть к доске выйдет Буратино с двумя купюрами в 1 и в 2 сольдо и хозяин гостиницы. Учитель комментирует события так:

– Буратино прожил в гостинице первый день и отдал хозяину 1 сольдо (Буратино дает хозяину купюру в 1 сольдо).

– Буратино прожил в гостинице второй день и отдал хозяину еще 1 сольдо (Буратино дает хозяину купюру в 2 сольдо и берет сдачу – купюру в 1 сольдо).

– Буратино прожил в гостинице третий день и отдал хозяину еще 1 сольдо (Буратино дает хозяину последнюю купюру в 1 сольдо).

Ответ: 1. В первый день отдать 1 сольдо, во второй отдать 2 сольдо и взять сдачу 1 сольдо, в третий день отдать 1 сольдо.

16. Отцу и сыну вместе 40 лет. Сколько будет им вместе через три года?

Решение. В этой задаче неизвестно, чему равны слагаемые: возраст отца и возраст сына. Однако, известна их сумма – 40 лет. Неизвестно и то, сколько будет лет каждому из них через 3 года. Но известно, что каждое слагаемое увеличится на 3, а значит, сумма увеличится на 3 + 3 = 6.

Значит, она станет равной 40 + 6 = 46.

Полезно изобразить решение на рисунке.

Ответ: 46 лет.

17. Один нехороший человек всегда говорит неправду. Что он ответит на вопрос: "Правдивы ли вы?"?

Ответ: "Да".

18. В доме отдыха 15 человек играют в уголки. Они провели между собой соревнование. После каждой партии выбывал проигравший. В первый день состоялось 5 партий, во второй 6, а в третий день соревнование закончилось. Сколько партий состоялось в третий день?

Решение. Выбыть должно 15 – 1 = 14 человек. Каждый из них выбывает в результате одной партии. Значит, партий должно быть 14. В третий день будет сыграно 14 – (5 + 6) = 3 партии.

Ответ: 3.

19. Сколько существует двузначных чисел, у которых все цифры четные?

Решение. На первом месте не может стоять нуль. Поэтому всего будет 4 х 5 = 20 чисел.

Ответ: 20 чисел.

20. Проживание за один день в сказочной гостинице стоит 1 сольдо. У Буратино имеются одна купюра в 1 сольдо и две купюры по 2 сольдо. Как он должен расплачиваться ежедневно за гостиницу на протяжении 5 дней?

Решение желательно проводить, как в задаче 19. Распределение купюр по дням видно из таблицы:

21. Мы знаем, что Вася родился с 15 по 18 июля. За сколько вопросов мы можем узнать его день рождения, если он согласен отвечать на наши вопросы только "да" или "нет". Каким может быть первый вопрос?

Решение. Нужно определить одно из 4 чисел. Это делается в два вопроса.

Ответ: 2. Первый вопрос может быть таким: "Ты родился с 15 по 16 июля?"

22. На двух полках стояло 25 книг. На каждую полку поставили еще столько книг, сколько было на другой полке. Сколько книг стало на двух полках после этого?

Решение. Обозначим число книг на первой полке римской цифрой I, а на второй – II. Тогда на первую полку поставили еще II книг, а на вторую еще I книг. Всего было книг I + II, а стало (I + II) + (II + I). Но нам известно, что I + II = 25. Значит, всего на двух полках стало 25 + 25 = 50 книг.

Ответ: 50 книг.

23. Ваня написал все числа от 1 до 1000. Сколько цифр написал Ваня?

Решение. Первые девять однозначных чисел написаны девятью цифрами. Двузначные числа от 10 до 99 требуют по две цифры. А так как этих чисел 90, то на их написание ушло 180 цифр. На 900 трехзначных чисел ушло 3 х 900 = 2700 цифр. И на число 1000 потрачено четыре цифры. Общее число написанных цифр равно 9 + 2 х 90 + 3 х 900 + 4 = 2893 цифры.

Ответ: 2893.

24. Гласные буквы расположили под согласными так:

б в г д ж з к л м н п р с т ф х ц ч ш щ

а е и о у ы э ю я а е и о у ы э ю я а е

Зашифруй, заменяя согласные гласными по этому правилу, фразу "Молоко полезно для здоровья". Как облегчить расшифровку этой фразы?

Ответ: яоюоэо еоюеыао оюя ыооиоеья. Расшифровку можно облегчить, подчеркнув те гласные, которые остались неизменными: яоюоэо еоюеыао оюя ыооиоеья.

25. Сколько существует трехзначных чисел, у которых все цифры нечетные?

Решение. На первое место можно поставить любую из пяти нечетных цифр, на второе – любое из пяти нечетных цифр, на третье – любое из пяти нечетных цифр. Итого чисел 5 х 5 х 5 = 125.

Ответ: 125 чисел

26. У продавца сколько угодно монет по 2 рубля и товары стоимостью 1, 2, 3, 4, 5, 6, 8 и 10 рублей. А у покупателя есть 2 монеты по 5 рублей. Докажи, что покупатель может купить любой из этих товаров, получив необходимую сдачу.

Решение. Лучше всего перечислить все необходимые 8 случаев. Это и будет требуемым доказательством.

27. У двух братьев вместе 100 марок. Старший брат подарил младшему на его день рождения 20 марок, и у них стало марок поровну. Сколько марок было у каждого брата до этого?

Решение.

1) Сколько марок стало у каждого после подарка? 100 : 2 = 50.

2) Сколько марок было у старшего брата до подарка? 50 + 20 = 70.

3) Сколько марок было у младшего брата до подарка? 50 – 20 = 30 ( или 100 – 70 = 30),

Ответ: 70 и 30.

28. Чему равно А: * х А = *А?

Решение. В этом ребусе однозначное число, обозначенное звездочкой, умножено на однозначное число А. Произведение – двузначное число, оканчивающееся на цифру А. А не равно 1, так как первый множитель однозначен, а произведение двузначно. А может равняться 2 в примере 6 х 2 = 12. А может равняться 4 в примере 6 х 4 = 24. А может равняться 5 в примерах 3 х 5 = 15, 5 х 5 = 25, 7 х 5 = 35 и 9 х 5 = 45. А может равняться 6 в примере 6 х 6 = 36. А может равняться 8 в примере 6 х 8 = 48.

Ответ: 2, 4, 5, 6 или 8.

29. В произведении чисел 24 и 12 второй множитель увеличили в два раза. Как изменилось произведение?

Решение. Конечно, можно решить задачу следующими вопросами.

1) Чему равно произведение данных чисел?

2) Чему стал равен второй множитель?

3) Чему стало равно произведение?

4) Во сколько раз изменилось произведение?

Собственно, так и нужно решать эту задачу, если ученики не понимают решения. Для этого и даны в задаче числовые данные. Но совсем хорошо решать задачу в общем виде, не используя лишних числовых данных. Это решение состоит в утверждении: если один из множителей не менять, а другой увеличить в два раза, то произведение увеличится в два раза.

Ответ: Произведение увеличилось в 2 раза.

30. Костя считает, что билет, купленный у кондуктора в автобусе или в трамвае, может приносить счастье. Для этого нужно, чтобы сумма первых трех цифр его шестизначного номера и сумма последних его цифр были равны между собой. Однажды в автобусе ему достался счастливый билет. Костя спрятал его. А когда потом вынул из кармана, то увидел, что последняя цифра стерлась. Первые же пять цифр были такие: 32875. Помоги Косте установить номер билета.

Решение. Номер билета выглядит так: 32875*. Так как билет счастливый, то 3 + 2 + 8 = 7 + 5 + *, откуда и получается ответ:

Ответ: 328751.

Задачи-шутки

1. На верёвке висели и спокойно сохли 8 выстиранных наволочек. 6 наволочек стащила с верёвки и сжевала коза Люська. Сколько наволочек спокойно высохли на верёвке?

2. Коза Люська забодала забор, который держался на 7 столбиках. 3 столбика упали вместе с забором, а остальные остались торчать самостоятельно. Сколько столбиков торчат самостоятельно?

3. Коза Люська имеет 4 кривые ноги, а её хозяйка Уля – только 2. Сколько всего ног у них обеих?

4. У первого петуха было 59 жён, а у второго – в 3 раза больше. На сколько жён больше, чем у первого петуха, стало у второго, после того, как первый женился ещё на трёх курицах?

5. В одной квартире преступники украли одну правую тапочку и две левые, а в другой – только одну правую. Сколько пар тапочек украли преступники в обеих квартирах?

6. В песочнице сидят 11 малышей. 9 малышей лепят куличики, а остальные лупят друг друга совочками. Сколько малышей лупят друг друга совочками?

7. На одной жужаре к нам прижакали 70 лямзиков, а на другой – на 3 лямзика больше. Сколько лямзиков прижакали к нам на обеих жужарах?

8. Одна фляка стоит 17 хмуриков. Сколько фляк можно купить на 85 хмуриков?

9. Мляша коллекционирует млянечки, а Пляша – плянечки. У Мляши млянечков в 3 раза больше, чем у Пляши плянечков. Сколько у Пляши плянечков, если у Мляши 69 млянечков?

10. Мряка и Бряка поссорились. Мряка 7 раз фрякнул Бряку марфуфочкой по чему попало, а Бряка фрякнул Мряку той же марфуфочкой по чему попало 9 раз. Спрашивается, сколько раз хватали бедную марфуфочку за хвост и фрякали ею по чему попало?

11. Если Хрямзика обозвать слюником, он начинает бодаться и не перестаёт, пока не боднет обозвавшего по 5 раз каждым рогом. Однажды Бряка именно так его и обозвала, и Хрямзик боднул её 35 раз. Сколько рогов у Хрямзика?

12. У трёх бабушек было по одному серенькому козлику. Бабушки козликов очень любили. Пошли козлики в лес погулять, а там их волк съел. Остались от козликов рожки да ножки. Сколько осталось рожек и сколько ножек?

13. Один дедушка охотился в кухне на тараканов и убил пятерых, а ранил – в три раза больше. Трёх тараканов дедушка ранил смертельно, и они погибли от ран, а остальные тараканы выздоровели, но обиделись на дедушку и навсегда ушли к соседям. Сколько тараканов ушли к соседям навсегда?

14. Сколько дырок окажется в клеёнке, если во время обеда 12 раз проткнуть её вилкой с 4 зубчиками?

15. В комнате веселилось 47 мух. Дядя Гоша открыл форточку, размахивая полотенцем, выгнал из комнаты 12 мух. Но прежде, чем он успел закрыть форточку, 7 мух вернулось обратно. Сколько мух теперь веселится в комнате?

16. У бабы Яги на носу 3 бородавки, а у Кощея Бессмертного – на 6 бородавок больше. Сколько бородавок теснится на носу у кощея Бессмертного?

17. У Змея Тугарина – одна голова, а у Змея Горыныча целых 3. На сколько голов Змей Горыныч умнее Змея Тугарина?

Математические ребусы