Максвелла как постулаты электродинамики
При рассмотрении электро- и магнитостатики определены теоретические объекты, которыми оперирует эти разделы электромагнетизма. Классическая (максвелловская) электродинамика – это теория переменного во времени электромагнитного поля. Разумеется, основными теоретическими объектами электродинамики являются те же объекты, что и в электро- и магнитостатике. Вспомним эти объекты:
1) точечное заряженное тело, обладающее электрическим зарядом q и инертной массой m. Единицей заряда служит кулон (Кл), 1Кл = 1А×1с;
2) электрический ток I точечных зарядов. Единица силы электрического тока - ампер (А) - относится к группе основных единиц системы СИ и для этой единицы существует соответствующий материализованный эталон;
3) электрическое поле (порождаемое зарядами и переменным магнитным полем). Основной характеристикой электрического поля является напряженность этого поля E. Единицей напряженности служит 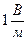 ;
;
4) магнитное поле, основной характеристикой которого является индукция магнитного поля B. Единицей магнитной индукции служит тесла (Тл): 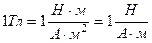 .
.
Теория электромагнитного поля констатирует, что в природе существует материальный объект – электромагнитное поле, которое представляет собой совокупность взаимосвязанных электрических и магнитных полей. Электромагнитное поле всегда находится в состоянии движения и распространяется в виде электромагнитной волны. Основные характеристики электромагнитного поля - векторы E и B - при переходе из одной системы отсчета в другую изменяются, и эти изменения происходят в соответствии с преобразованиями Лоренца (не Галилея!), т.к. электромагнитное поле движется с релятивистской скоростью (со скоростью света). Если в некоторой системе отсчета (назовем ее первой) наблюдается чисто электростатическое или чисто магнитостатическое поле, то в другой системе, движущейся относительно первой, будет наблюдаться как электрическое, так и магнитное поля.
Научные факты, полученные в результате экспериментальных исследований явлений электромагнетизма в макромире, нашли свое содержательное теоретическое обобщение в системе из четырех уравнений, носящих имя Д.К. Максвелла. Уравнения Максвелла дополнены уравнениями связи, отражающими свойства среды, в которой распространяется электромагнитная волна.
Уравнения Максвелла образуют систему фундаментальных постулатов классической электродинамики (электродинамики Максвелла), описывающих все многообразие электромагнитных явлений в макромире. Электромагнитные явления в микромире описываются другой физической теорией - квантовой электродинамикой.
В зависимости от решаемых задач, уравнения Максвелла могут быть записаны в интегральной, дифференциальной, комплексной форме.
Интегральная форма уравнений Максвелла фактически представляет собой систему непосредственных теоретических обобщений результатов решающих экспериментов электромагнетизма. К этим экспериментам относятся: опыты Кулона и Кавендиша по исследованию закона взаимодействия зарядов; опыты Эрстеда по обнаружению источника магнитного поля; факт отсутствия в природе элементарных частиц, обладающих магнитным зарядом (точнее, факт не обнаружения таких частиц в природе); опыты Фарадея по исследовании явления электромагнитной индукции; факт существования переменного электрического тока в цепи с конденсатором и ряд других экспериментов.
Дифференциальная форма уравнений Максвелла используется при решении большинства задач электродинамики. Эта форма позволяет естественным образом описывать пространственно-временные характеристики электромагнитных процессов, в том числе излучение, распространение и прием электромагнитных волн.
Комплексная форма уравнений Максвелла оперирует комплексными амплитудами векторовE, B, плотности тока j и других векторов и скалярных величин. Эта форма используется при описании чисто пространственных характеристик электромагнитной волны.
Вначале рассмотрим уравнения Максвелла в интегральной и дифференциальной форме.  Основными характеристиками электромагнитного поля являются вектор напряженности электрического поля E и вектор индукции магнитного поля B. Пространственная конфигурация векторов E и B,т.е. направление и изменение E и B в пространстве, наглядно отображаются с помощью силовых линий. Напомним, векторы напряженности E и индукции B направлены по касательной к своим силовым линиям, а изменение густоты силовых линий показывает относительное изменение модуля этих векторов (рис. 3-24).
Основными характеристиками электромагнитного поля являются вектор напряженности электрического поля E и вектор индукции магнитного поля B. Пространственная конфигурация векторов E и B,т.е. направление и изменение E и B в пространстве, наглядно отображаются с помощью силовых линий. Напомним, векторы напряженности E и индукции B направлены по касательной к своим силовым линиям, а изменение густоты силовых линий показывает относительное изменение модуля этих векторов (рис. 3-24).
Способ отображения полей с помощью силовых линий будет использован при раскрытии содержания уравнений Максвелла.
3.4.2. Интегральная теорема Гаусса и дивергенция электрического и
Магнитного полей
В систему уравнений Максвелла входят, как было уже отмечено, четыре уравнения. Из этих четырех уравнений два уравнения уже нами ранее рассмотрены, это: 1) теорема Гаусса о потоке электростатического поля и соответствующая дифференциальная форма этой теоремы; 2) теорема Гаусса о потоке магнитного поля и соответствующая дифференциальная форма теоремы.
Повторимся. Основной характеристикой электрического поля является вектор напряженности поляE. Для описания поля в среде c диэлектрической проницаемостью e вводится вспомогательная величина - вектор смещения D =ee0E. Аналогично, основной характеристикой магнитного поля является вектор индукции магнитного поля B, а для описания магнитного поля в магнетиках с магнитной проницаемостью m вводится вспомогательная величина - вектор напряженности магнитного поля H (B= mm0 H). Естественно, теорема Гаусса записывается как для основных, так и вспомогательных векторов.
В целях удобного обзора напишем эти уравнения еще раз.
1. Интегральная теорема Гаусса о потоке вектора напряженности E электростатического поля через замкнутую поверхность:
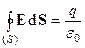 или
или 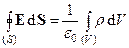 . (1)
. (1)
где q (или q = 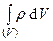 ) - алгебраическая сумма всех зарядов (свободных и связанных) внутри замкнутой поверхности S. Дифференциальная форма теоремы (1):
) - алгебраическая сумма всех зарядов (свободных и связанных) внутри замкнутой поверхности S. Дифференциальная форма теоремы (1):
div E = 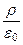 или ÑE =
или ÑE = 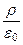 . (2)
. (2)
Дивергенция инвариантна относительно преобразования координат. В частности, дивергенцияE относительно декартовой системы координат запишется в виде: 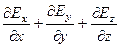 =
= 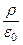 .
.
Теорема Гаусса для вектора смещенияD =ee0E:
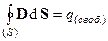 или
или 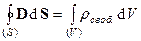 , (3)
, (3)
где rсвоб. – плотность свободных зарядов внутри замкнутой поверхности S. Дифференциальная форма теоремы (3):
ÑD = rсвоб. (4)
В декартовой системе дивергенция D имеет вид:
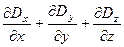 =rсвоб.
=rсвоб.
2. Интегральная теорема Гаусса о потоке вектора индукции B магнитного поля через замкнутую поверхность.
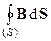 = 0. (5)
= 0. (5)
Соответствующая дифференциальная форма уравнения (4.5) запишется в виде: div B = 0 или ÑB = 0. (6)
Относительно декартовой системы координат дивергенция B имеет вид:
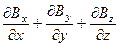 = 0.
= 0.
Можно записать также и интегральную теорему Гаусса для вектора напряженности магнитного поля H:
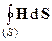 = 0. (7)
= 0. (7)
Соответствующая дифференциальная форма уравнения (4.7) имеет вид:
div H = 0 или ÑH = 0. (8)
Относительно декартовой системы координат дивергенция H имеет вид:
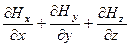 = 0.
= 0.
3.4.3. Циркуляция и ротор вихревого электрического поля
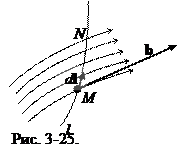 1. Вначале подробнее остановимся на понятии циркуляции вектора. Допустим задано некоторое векторное поле b(x, y, z). На рис. 3-25 показаны силовые линии поля и вектор b в точке M(x, y, z) этого поля. Проведем в векторном поле через точку M некоторую дугу l (дуга может и не совпадать с силовой линией). Направление элементарного перемещения по дуге (здесь в направлении от M к N) определим вектором dl. Модуль dl является дифференциалом дуги. Из векторов bи dl можно образовать скалярное произведение: (b×dl).
1. Вначале подробнее остановимся на понятии циркуляции вектора. Допустим задано некоторое векторное поле b(x, y, z). На рис. 3-25 показаны силовые линии поля и вектор b в точке M(x, y, z) этого поля. Проведем в векторном поле через точку M некоторую дугу l (дуга может и не совпадать с силовой линией). Направление элементарного перемещения по дуге (здесь в направлении от M к N) определим вектором dl. Модуль dl является дифференциалом дуги. Из векторов bи dl можно образовать скалярное произведение: (b×dl).
Содержание этого скалярного произведения в различных векторных полях различно. Например, если в качестве вектора bвзять вектор силы F, то скалярное произведение (F×dl) есть элементарная работа силы F на перемещении dl.
Интеграл по дуге l от точки M до точки N
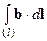 =
= 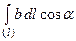 =
= 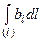
называется криволинейным интегралом. Здесь: a - угол между векторамиb и dl; bl – проекция b на направление вектора dl.
Криволинейный интеграл 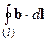 , взятый по замкнутому контуру l, называется циркуляцией вектора b.
, взятый по замкнутому контуру l, называется циркуляцией вектора b.
Ранее мы выяснили, что циркуляция напряженности E электростатического поля равна нулю (§ 3.1.8). Вспомним, это можно показать, воспользовавшись фактом равенства нулю работы A электростатического поля при движении заряда q по замкнутому контуру l:
A = 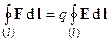 = 0, поэтому
= 0, поэтому 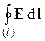 = 0. (9)
= 0. (9)
2. Циркуляция вихревого электрического поля. Опыты Фарадея по электромагнитной индукции показали, что переменное во времени магнитное поле порождает в пространстве вихревое электрическое поле. Силовые линии этого поля замкнуты сами на себя. Циркуляция вихревого электрического поля по любому контуру определяется выражением
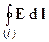 =
= 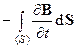 . (10)
. (10)
 Знак минус отражает правило Ленца. Частная производная
Знак минус отражает правило Ленца. Частная производная 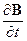 подчеркивает, что произвольный контур l и натянутая на контур произвольная поверхность S неподвижны.
подчеркивает, что произвольный контур l и натянутая на контур произвольная поверхность S неподвижны.
Иллюстрация уравнения Максвелла (10) приведена на рис. 3-26, где показана поверхность S, ограниченная контуром l, и переменное магнитное поле (вектор 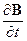 ), пронизывающее поверхность S. Подчеркнем, контур l и охватываемая им поверхность S могут быть любой формы. В общем случае в разных точках поверхности S векторы
), пронизывающее поверхность S. Подчеркнем, контур l и охватываемая им поверхность S могут быть любой формы. В общем случае в разных точках поверхности S векторы 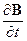 могут различаться по модулю и составлять с поверхностью некоторый угол. Направление вектора E определено правилом правого винта с учетом правила Ленца.
могут различаться по модулю и составлять с поверхностью некоторый угол. Направление вектора E определено правилом правого винта с учетом правила Ленца.
Кольцо из проводника (материализованный контур), находящийся в переменном магнитном поле, позволяет экспериментально обнаружить вихревое электрическое поле по индуцированному в этом кольце электрическому току.
Напомним следующее. Согласно закону Фарадея 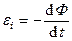 , ЭДС индукции ei в проводнике (например, в форме кольца) возникает при изменении во времени магнитного потока Ф = BS =B S cosα, пронизывающего кольцо. Каквидно из выражения для потока, изменять магнитный поток Ф с течением времени можно тремя способами:
, ЭДС индукции ei в проводнике (например, в форме кольца) возникает при изменении во времени магнитного потока Ф = BS =B S cosα, пронизывающего кольцо. Каквидно из выражения для потока, изменять магнитный поток Ф с течением времени можно тремя способами:
1) используя переменное магнитное поле (изменяя во времени индукцию магнитного поля B); 2) изменяя площадь кольца S в постоянном магнитном поле, деформируя кольцо; 3) изменяя угол α между векторамиBиS, вращая кольцо в постоянном магнитном поле.
Деформация кольца и изменение угла α означают, что соответствующий контур подвижен. Возникновение ЭДС x в процессе деформации кольца или изменения угла α обусловлено действием силы Лоренца на заряды (электроны, ионы) в движущихся частях проводника.
В уравнении Максвелла (10) контур l и натянутая на контур поверхность S неподвижны (взята частная производная 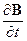 ). Уравнение (10) отражает фундаментальный факт: переменное во времени магнитное поле
). Уравнение (10) отражает фундаментальный факт: переменное во времени магнитное поле 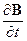 порождает вихревое электрическое поле E
порождает вихревое электрическое поле E
Итак, констатируем, источником электрического поля могут быть:
1) неподвижные заряды, являющиеся источником электростатического поля; циркуляция электростатического поля равна нулю – уравнение (9);
2) переменное во времени магнитное поле, порождающее вихревое электрическое поле; циркуляция вихревого электрического поля не равна нулю и определяется уравнением (10). Силовые линии вихревого электрического поля охватывают вихри в виде переменного магнитного поля 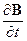 (вихри расположены на поверхности S).
(вихри расположены на поверхности S).
3. Дифференциальная форма уравнения о циркуляции вихревого электрического поля. Ротор вектора E.
Важным в понимании дифференциальной формы уравнения Максвелла о циркуляции электрического поля является то обстоятельство, что циркуляция вектораEпорождается на поверхности S, натянутого на контур. Действительно, из уравнения (10) следует, что циркуляция по контуру l равна интегралу всех 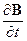 на поверхности S, ограниченной контуром l.
на поверхности S, ограниченной контуром l.
Так как циркуляция порождается на поверхности, то можно говорить о плотности циркуляции в точке (x, y, z) на поверхности S и ввести соответствующую характеристику векторного поля. Эта характеристика называется ротором (вихрем) векторного поля.
Раскроем содержание понятия ротора (вихря) векторного поля E, характеризующего плотность циркуляции в выбранной точке поверхности S.
Введем понятие средней плотности порождения циркуляции на поверхности Sкак отношения циркуляции к площади S:
средняя плотность циркуляции E на поверхности = 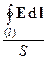 .
.
Рассмотрим на поверхности S некоторую точку M с координатами (x,y,z) и будем стягивать контур l к этой точке. При этом контур все время должен оставаться на поверхности S. Получаемая при стягивании контура бесконечно малая поверхность dS содержит точку M(x,y,z). Предел, к которому стремится средняя плотность циркуляции при стягивании контура к точке M(x,y,z), определяет плотность порождения циркуляции в этой точке M(x,y,z):
плотность циркуляции в точке M(x,y,z) = 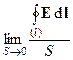 . (11)
. (11)
Плотность циркуляции (скалярная величина!) равна проекции некоторого вектора на направление нормали n к элементарной поверхности dS, содержащей данную точку M(x,y,z). Покажем это, воспользовавшись примером, приведенным в книге: Савельев И.В. Курс общей физики в 5 книгах. Кн.2. Электричество и магнетизм. – М.: Наука, 1998, с. 50-61.
Циркуляция однородного электрического поля, т.е. поля при E = const, равна нулю: 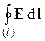 =
= 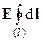 = 0, т.к. сумма замыкающихся на себя векторов равна нулю:
= 0, т.к. сумма замыкающихся на себя векторов равна нулю: 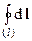 =0. Рассмотрим циркуляцию неоднородного электрического поля.
=0. Рассмотрим циркуляцию неоднородного электрического поля.
Пусть электрическое поле направлено перпендикулярно плоскости Z0Y (на рис. 3-27-а ось 0Z направлена к нам). У такого неоднородного поля отлично от нуля только компонента Ex, следовательно,E = Exi. Допустим, неоднородность поля выражена тем, что компонента Ex линейно растет с координатой y, т.е. компоненту Ex можно представить линейной функцией Ex = ky, где k = const (единица измерения k - 1В/м2). На рис. 3-27-а неоднородностьE отображена изменением густоты силовых линийE с изменением y. Итак, имеем:
E = Exi = kyi.
Определим циркуляциюE по элементарному контуру (1-2-3-4) в форме квадрата со сторонами 2а и площадью контура dS = 4a2 (чтобы определить плотность циркуляции в рассматриваемой точке, необходимо взять бесконечно малый контур). Центр контура имеет по оси 0Y координату y.
Пусть вначале плоскость, охватываемая контуром, параллельна координатной плоскости X0Y , а стороны квадраты (1-4) и (2-3) параллельны оси 0Y.
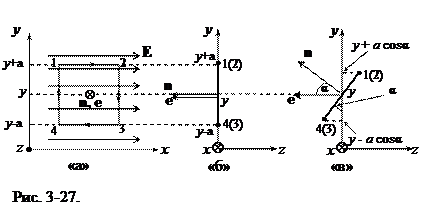 |
В соответствии с выбранным направлением обхода контура, положительная нормаль n к плоскости контура направлена на рис. 3-27-а от нас за чертеж (правило правого винта). На этом же рис. 3-27-а показан фиксированный в данной системе координат единичный вектор e, перпендикулярный плоскости контура и также направленный за чертеж. С помощью фиксированного вектора e будем определять изменение ориентации плоскости контура в выбранной системе координат. Если повернуть плоскость контура, то этот поворот оценивается соответствующим углом между n и e. Рис. 3-27-а дублирован рисунком 3-27-б (на рисунке координатная система рассматривается со стороны координатной плоскости Y0Z и ось 0X на рисункенаправлена от нас). Циркуляция вектора Eпо данному контуруравна (см. рис. 3-27-а):
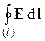 = Exl1-2 + Exl2-3cos900 + Exl3-4 cos1800 + Exl4-1cos900 =
= Exl1-2 + Exl2-3cos900 + Exl3-4 cos1800 + Exl4-1cos900 =
= k(y + a)2a - k(y - a)2a = k4a2 = k dS,
где dS = 4a2 – площадь, охватываемая элементарным контуром. Заметим, так как циркуляция не равна нулю, то это не электростатическое поле.
Поделив, в соответствии с определением плотности циркуляции (11), полученный результат циркуляции(k dS) на площадь dS, получим плотность циркуляции, которая здесь равна k.
Определим циркуляцию относительно того же контура, но повернутого на угол α относительно оси, параллельной 0X и проходящей через середину контура (рис. 3-27-в). В этом случае стороны квадрата (1-4) и (2-3) образуют угол α с направление оси 0Y. Нормаль n к поверхности контура также повернется на угол α относительно фиксированного вектора e. Имеем:
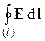 = k(y + a cosα)2a - k(y – a cosα)2a = k4a2 cosα = k dS cosα.
= k(y + a cosα)2a - k(y – a cosα)2a = k4a2 cosα = k dS cosα.
В этом случае плотность циркуляции равна 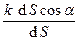 = k cosα.
= k cosα.
Образуем вектор ke. Скалярное произведение ke×n равно проекции вектора ke на нормаль n: ke×n = k cosα.
Из приведенного примера следует, что, плотность циркуляции на поверхности ведет себя как проекция вектора keна нормальnк поверхности, ограниченного контуром. В частности, при α = 0 проекция равна k. Вектор ke называется ротором (или вихрем) векторного поля. Ротор обозначается символом rot. В нашем примере
rot E= ke, а модуль ротора равен k.
Проекция rot E на n в нашем примере: (rot E)n = k cosα .
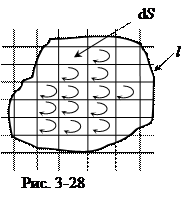 Итак, плотность циркуляции -
Итак, плотность циркуляции - 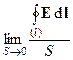 - в данной точке поверхности S, натянутой на контур, является проекцией ротора E на положительную нормаль n к поверхности: (rot E)n =
- в данной точке поверхности S, натянутой на контур, является проекцией ротора E на положительную нормаль n к поверхности: (rot E)n = 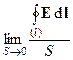 . (12)
. (12)
Еще раз отметим, циркуляция порождается на поверхности контура. Плотность циркуляции максимальна и равна модулю вектора rot E, когда направление ротора совпадает с направлением нормали n. Можно, соответственно, говорить о потоке вектора rot Eчерез поверхность элементарного контура.
Теорема Стокса. Рассмотрим важную интегральную теорему векторного анализа – теорему Стокса. Пусть конечный контур l охватывает поверхность S. Разобьем S на бесконечно малые элементарные площадки dS, охватываемые элементарными контурами dl (рис. 3-28).
Из (12) следует: 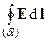 =
= 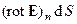 или
или 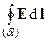 =
= 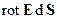 ,
,
где: dS = ndS; dl – здесь это элемент бесконечно малого контура dl. Скалярное произведение ( 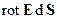 ) является потоком вектора rot Eчерез элементарную площадку dS. Просуммировав (
) является потоком вектора rot Eчерез элементарную площадку dS. Просуммировав ( 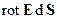 ) по всем dS, получим в пределе интеграл по всей поверхности S. Этот интеграл определяет поток ротора через конечную поверхность S:
) по всем dS, получим в пределе интеграл по всей поверхности S. Этот интеграл определяет поток ротора через конечную поверхность S:
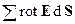 =
= 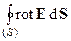 .
.
Сумма циркуляций 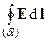 по элементарным контурам dl приводит к циркуляции по контуру l, охватывающему поверхность S (сумма циркуляций от внутренних контуров равна нулю, т.к. при суммировании они входят дважды с противоположными знаками):
по элементарным контурам dl приводит к циркуляции по контуру l, охватывающему поверхность S (сумма циркуляций от внутренних контуров равна нулю, т.к. при суммировании они входят дважды с противоположными знаками):
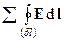 =
= 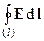
Приходим к уравнению: 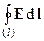 =
= 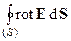 (13)
(13)
Уравнение (13) называется теоремой Стокса. Теорема Стокса (13) утверждает: циркуляция вектора E по произвольному контуру l равна потоку rot Eчерез произвольную поверхность S, ограниченную этим контуром. Теорема связывает поверхностный интеграл с интегралом по контуру. В этом смысле теорема Стокса аналогична теореме Гаусса-Остроградского [см. § 3.1.3, уравнение (1.9)], связывающего объемный интеграл с интегралом по поверхности.
В соответствии с интегральным уравнением Максвелла (10), вихревое электрическое поле порождается переменным магнитным полем. Запишем интегральное уравнение Максвелла (10) еще раз здесь:
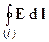 =
= 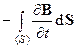 .
.
Сравнивая интегральное уравнение Максвелла с теоремой Стокса (13), получаем дифференциальную форму этого уравнения Максвелла:
rot E = - 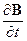 . (14)
. (14)
Ротором (вихрем) электрического поля является взятая с обратным знаком переменная во времени индукция магнитного поля 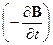 . Ротор
. Ротор 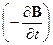 порождает циркуляцию E. Напомним, модуль ротора равен максимальной плотности циркуляции электрического поля в данной точке. Максимальная плотность циркуляции реализуется при условии, когда ротор перпендикулярен поверхности (параллелен нормали n к поверхности).
порождает циркуляцию E. Напомним, модуль ротора равен максимальной плотности циркуляции электрического поля в данной точке. Максимальная плотность циркуляции реализуется при условии, когда ротор перпендикулярен поверхности (параллелен нормали n к поверхности).
4.Явный вид ротора (14) в декартовой системе координат.Запишем ротор в декартовой системе координат:
rot E= (rot E)xi + (rot E)yj + (rot E)zk. (15)
Раскроем явный вид, например, компоненты (rot E)x.
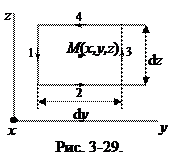 Так как задача заключается в определении x-компоненты ротора, то выберем элементарный контур в виде прямоугольника, параллельного плоскости Y0Z, а нормаль n к плоскости контура направим в положительном направлении оси 0х (на рис. 3-29 ось 0х направлена к нам). При таком направлении вектора n обход контура на рисунке осуществляется против часовой стрелки. Циркуляция по элементарному контуру будет определяться выражением:
Так как задача заключается в определении x-компоненты ротора, то выберем элементарный контур в виде прямоугольника, параллельного плоскости Y0Z, а нормаль n к плоскости контура направим в положительном направлении оси 0х (на рис. 3-29 ось 0х направлена к нам). При таком направлении вектора n обход контура на рисунке осуществляется против часовой стрелки. Циркуляция по элементарному контуру будет определяться выражением:
(Ez3dz - Ez1dz) + (Ey2dy - Ey4dy),
Здесь учтено, что на участках контура (1) и (4) направление обхода противоположно положительным направлениям, соответственно, осей 0z и 0y. На двух других – направления совпадают. Представим выражение для циркуляции в виде:
(Ez3 - Ez1) dz - (Ey4 - Ey2) dy.
Величина (Ez3 - Ez1) – приращение Ez на отрезке dz при смещении этого отрезка на dy. Это приращение можно представить при стягивании контура в точку M(x,y,z) в виде
(Ez3 - Ez1) = 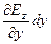 .
.
Аналогично, (Ey4 - Ey2) – приращение Ey на отрезке dy при смещении этого отрезка на dz. Это приращение принимает вид:
(Ey4 - Ey2) = 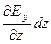 .
.
Подставим полученные соотношения в исходное выражение, получим циркуляцию по элементарному контуру:
( 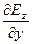 -
- 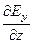 ) dy dz или (
) dy dz или ( 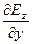 -
- 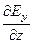 ) dS,
) dS,
где dS = dy dz – площадь элементарного контура.
Плотность циркуляции, т.е. (rot E)x, определяется деление циркуляции на площадь контура [см. (12)]. Разделив циркуляцию на площадь контура, получим выражение для компоненты (rot E)x относительно декартовой системы координат:
(rot E)x = 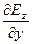 -
- 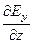 .
.
Аналогично получаются выражения для остальных двух компонент:
(rot E)y = 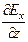 -
- 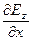 ,
,
(rot E)z = 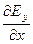 -
- 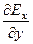 .
.
Таким образом, уравнение Максвелла (14) в декартовой системе координат имеет вид:
( 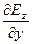 -
- 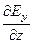 )i+ (
)i+ ( 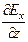 -
- 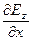 )j+ (
)j+ ( 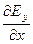 -
- 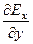 )k = -(
)k = -( 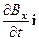 +
+ 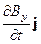 +
+ 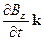 ) (16)
) (16)
Далее нам понадобиться операция векторного произведения векторов. Векторное произведение, например, векторов a и b, будем обозначать символом [a, b], т.е. сомножители поставлены в квадратных скобках через запятую. Приведем форму записи уравнения Максвелла (16) с использованием векторного оператора Гамильтона (оператора набла). Умножим векторно оператор набла Ñ = 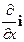 +
+ 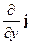 +
+ 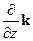 на напряженность электрического поля E = Ex i+ Ey j + Ez k,получим:
на напряженность электрического поля E = Ex i+ Ey j + Ez k,получим:
[Ñ, E] = [( 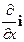 +
+ 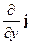 +
+ 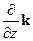 ), ( Exi+ Eyj + Ez k)] =
), ( Exi+ Eyj + Ez k)] =
= ( 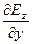 -
- 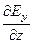 )i+ (
)i+ ( 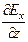 -
- 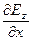 )j+ (
)j+ ( 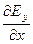 -
- 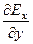 )k.
)k.
Полученное выражение есть ротор вектора E в декартовой системе. Выражение [Ñ, E] читается: ротор вектора E. Теперь уравнение Максвелла (14) можно записать также и в форме:
[Ñ, E] = - 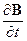 . (17)
. (17)
Отметим, ротор, как и дивергенция, инвариантен относительно выбора системы координат.
3.4.4.Циркуляция и ротор магнитного поля. Гипотеза Максвелла
1.Циркуляция магнитного поля, создаваемого постоянным электрическим током. Теорема о циркуляции вектора индукции B магнитного поля тока, рассмотренного в § 3.2.4, является теоретическим обобщением опытов Эрстеда:
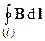 =m0 I или
=m0 I или 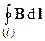 =
= 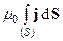 . (18)
. (18)
Соответственно, теорема о циркуляции вектора напряженности магнитного поля имеет вид: 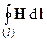 = I или
= I или 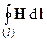 =
= 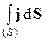 . (19)
. (19)
Напомним: циркуляция вектора B определяется всеми токами в магнетике – и токами проводимости и токами намагничивания; циркуляция вектора H зависит только от токов проводимости.
2. Гипотеза Максвелла.
Исходя из идеи о единстве электрического и магнитного явлений и аналогии с явлением электромагнитной индукции, Максвелл выдвинул гипотезу о том, что источником магнитного поля являются не только электрические токи, но и переменное электрическое поле.
Идея о единстве природы электрического и магнитного явлений была высказана многими физиками задолго до Д.К. Максвелла. Можно вспомнить, например, доклад на тему «Речь о сходстве электрической и магнитной силы» Ф. Эпинуса, помощника М.В. Ломоносова, прочитанный им в 1758 году. Опыты Фарадея по электромагнитной индукции убедили, что переменное магнитное поле порождает электрическое поле. Максвелл выдвинул гипотезу, что в природе реализуется и обратный процесс – переменное электрическое поле должно порождать магнитное поле.
Ток смещения. Гипотезу Максвелла можно проиллюстрировать, например, рассмотрев факт существования переменного электрического тока в цепи, в которой имеется конденсатор.
Предварительно получим уравнение непрерывности в цепи с электрическим током. Выделим внутри проводника, по которому течет электрический ток свободных зарядов, объем V, ограниченный поверхностью S. Поток плотности тока проводимости j из этого объема равен свободным зарядам, выходящим за единицу времени через поверхность S, т.е. равен убыли заряда в единицу времени в объеме V:
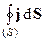 =
= 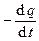 . (20)
. (20)
Уравнение (4.20) отражает закон сохранения заряда и называется уравнением непрерывности.
В случае постоянного тока концентрация зарядов в выделенном объеме не изменяется, - сколько зарядов в единицу времени войдет в выделенный объем, столько же за это же время выйдет. Уравнение непрерывности в случае постоянного тока принимает вид 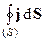 = 0. (20*)
= 0. (20*)
Из этого следует, что линии вектора плотности постоянного токаj замкнуты сами на себя. Таким образом, исходным условием существования постоянного тока является замкнутая цепь. В частности, если в какой-то ветви (части) цепи постоянного тока содержится конденсатор, то в этой ветви ток отсутствует, так как конденсатор представляет собой разрыв цепи.
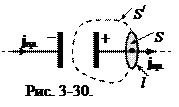 В цепи переменного тока с конденсатором электрический ток существует и может быть измерен амперметром. Подробнее рассмотрим циркуляцию магнитного поля, создаваемого переменным током в ветви цепи, содержащий конденсатор (рис. 3-30). В качестве контура l возьмем замкнутую кривую, охватывающую провод, соединенный с конденсатором. Циркуляция H равна потоку тока проводимости через поверхность S, натянутую на контур (19).
В цепи переменного тока с конденсатором электрический ток существует и может быть измерен амперметром. Подробнее рассмотрим циркуляцию магнитного поля, создаваемого переменным током в ветви цепи, содержащий конденсатор (рис. 3-30). В качестве контура l возьмем замкнутую кривую, охватывающую провод, соединенный с конденсатором. Циркуляция H равна потоку тока проводимости через поверхность S, натянутую на контур (19).
Как было рассмотрено ранее, циркуляция порождается на поверхности, натянутой на контур, и циркуляция не зависит от субъективного выбора формы поверхности. Важно только, чтобы существовал источник циркуляции на поверхности: поверхность должна пронизываться электрическим током. На рисунке приведены две поверхности S и S/, натянутые на один и тот же контур l. Через поверхность S проходит электрический ток (мысленная поверхность S пересекает провод) и уравнение (19) выполняется. Через поверхность S/ ток проводимости отсутствует, и уравнение (19) не выполняется. Получается, что циркуляция зависит от субъективного выбора формы поверхности, что не должно быть. Возникшее противоречие может быть обусловлено только тем, что не учтены особенности поверхности S/, точнее - не учтены особенности пространства между обкладками конденсатора.
Поверхность S/ пронизывается переменным электрическим полем, создаваемым зарядами на обкладках конденсатора (заряды на обкладках периодически изменяются по величине и знаку, т.к. ток переменный). Поток вектора D= ee0E через замкнутую поверхность (S/ + S), охватывающую правую обкладку конденсатора, определяется теоремой Гаусса [§ 3.1.2 (5*)]. Продифференцируем по времени теорему Гаусса, получим:
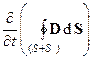 =
= 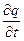 .
.
Полученное уравнение гласит, что изменение потока вектора Dопределяетсяизменением заряда внутри замкнутой поверхности (S/ + S). Поменяем последовательность операций дифференцирования и интегрирования, получим:
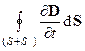 =
= 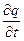 , (21)
, (21)
где размерность интеграла 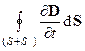 совпадает с размерностью тока и измеряется в амперах,
совпадает с размерностью тока и измеряется в амперах, 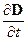 имеет размерность плотности тока, измеряется в А/м2.
имеет размерность плотности тока, измеряется в А/м2.
