Вычисление площади с помощью криволинейного интеграла второго рода
В п.2.5.было установлено, что работа силового поля при перемещении материальной точки вдоль кривой Г выражается криволинейным интегралом второго рода по этой кривой. Применение криволинейного интеграла второго рода к решению физических задач будет изложено в теории поля. Покажем, что криволинейный интеграл может быть использован для вычисления площади плоской фигуры. Пусть D-некоторая область (правильная) с границей L и S- площадь этой области. Рассмотрим криволинейный интеграл 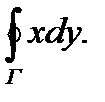 Применив к нему формулу Грина, где
Применив к нему формулу Грина, где 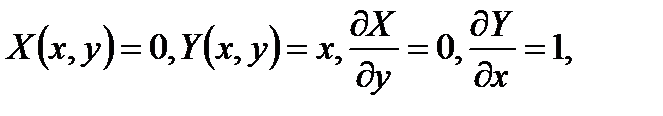 получим
получим
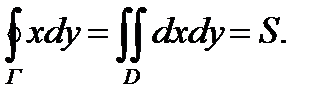

Аналогично получается другая формула
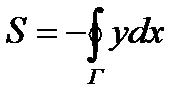
Можно получить иные формулы. Для этого достаточно выбрать функции 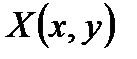 и
и 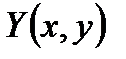 такими, чтобы они удовлетворяли условию
такими, чтобы они удовлетворяли условию
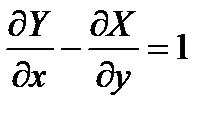
Так, если в интеграле 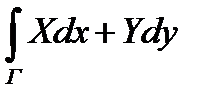 положить
положить 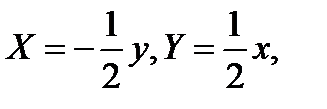 то
то 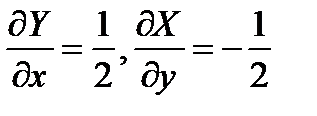 и
и
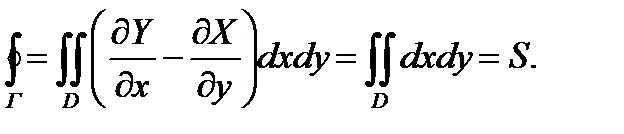
Следовательно,
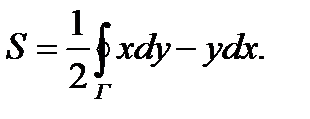
(1)
Формула (1) отличается от предыдущих двух симметричностью формы.
ПРИМЕР 1. Вычислить площадь области, ограниченной астроидой 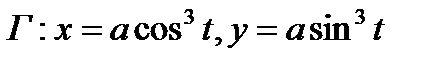 (см. рис.16). Применяя формулу (1), получим
(см. рис.16). Применяя формулу (1), получим
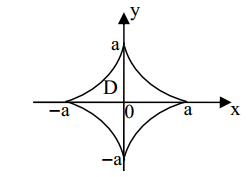
Рис.16. К примеру 1.
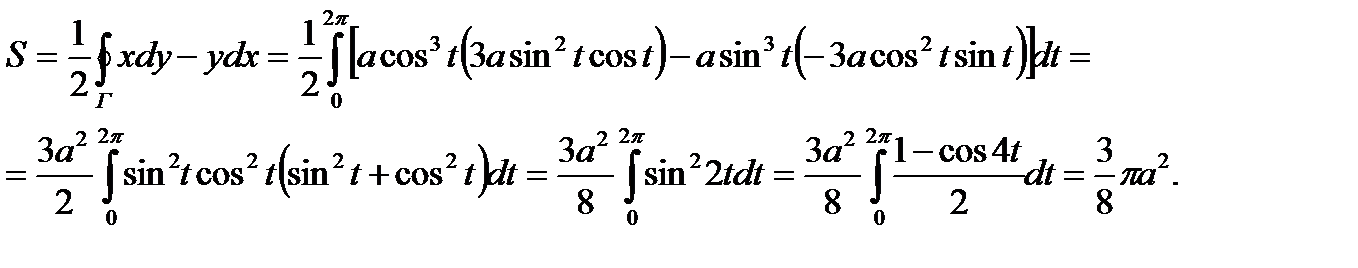



Формула Грина.
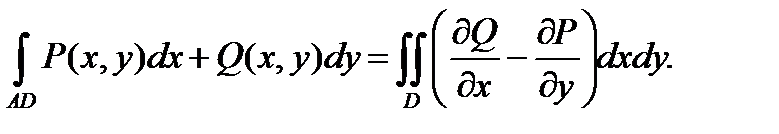
Если D - односвязная область, тоAD (граница области D) - простая замкнутая кривая, обход по которой совершается против часовой стрелки. Если D – неодносвязна, то AD- совокупность замкнутых кривых, обход по которым совершается так, что D остается слева.
Первообразная дифференциального выражения
Если в односвязной области D для функций P и Q выполняется условие Эйлера 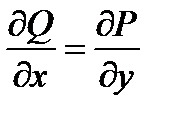 , то дифференциальное выражение
, то дифференциальное выражение 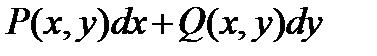 является полным дифференциалом, т. е. существует функции
является полным дифференциалом, т. е. существует функции 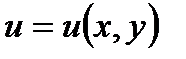 (первообразная), такая, что
(первообразная), такая, что 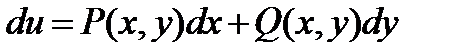 всюду в области D. Первообразная может быть вычислена по одной из формул:
всюду в области D. Первообразная может быть вычислена по одной из формул:
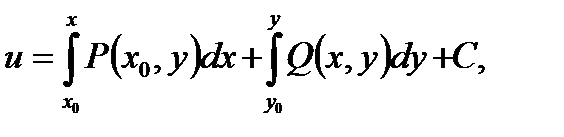
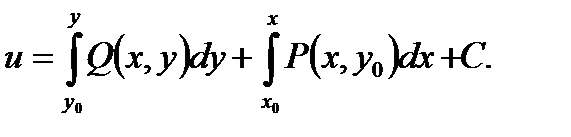
Криволинейный интеграл второго рода от выражения, являющегося полным дифференциалом, не зависит от формы пути, соединяющего точки 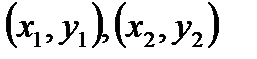 и может быть вычислен с помощью формулы двойной подстановки:
и может быть вычислен с помощью формулы двойной подстановки:
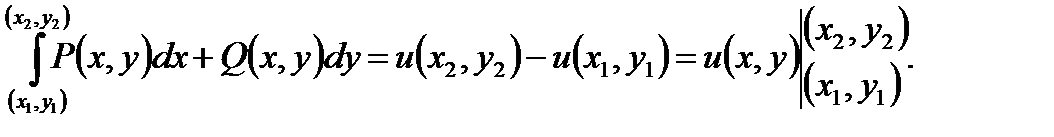
Заключение
В данной курсовой работе на тему «Геометрическое и физическое применение криволинейных интегралов» мы рассмотрели основные теоретические сведения необходимые для глубокого понимания данной темы, а также их применение к решению прикладных задач. С помощью теории криволинейных интегралов изложено нахождение площадей, ограниченных различными кривыми, объёмов, ограниченных различными поверхностями, в том числе нахождение площадей и объёмов тел вращения. А также описано нахождение длины дуги заданной кривой на данном отрезке. Представлены некоторые механические приложения для криволинейных интегралов: нахождение статических моментов, координат центра тяжести кривой, плоской и объёмной фигур, масса кривой с переменной линейной плотностью. Приведены физические приложения, например, нахождение механической работы, работы силового поля и притяжение материальной точки материальной кривой. В работе приведены некоторые применения криволинейных и поверхностных интегралов. Также в ней подробно разобраны наглядные примеры на применение криволинейного интеграла первого и второго рода.
Значимость данной курсовой работы заключается в систематизации материала. Данная работа может быть использована в качестве пособия для самостоятельного изучения данной темы.
Список литературы
1. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. Серия "Математика в техническом университете", вып. 9. М.: МГТУ, 2001.
2. Краснов М.Л., Киселев А.И., и др. Вся высшая математика. Элементы теории поля. Серия "Математика в техническом университете", Т. 4. М.: УРСС, 2000.
3. Кудрявцев Л.Д. Курс математического анализа. Том 2. М.: Дрофа, 2003.
4. Мельников Д.А., Неклюдов А.В., Титов К.В. Криволинейные и поверхностные интегралы. Методические указание к выполнению типового расчета поля. МГТУ, 2002.
5. Соболев С.К., Ильичев А.Т. Исследование и построение плоских кривых, заданных параметрически в полярных координатах. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2004. - 80 с.
