Метод конечных элементов. Метод конечных разностей

Метод конечных разностей

Рассмотрим основные понятия метода конечных разностей (МКР) на примере наиболее простого уравнения – уравнения переноса величины 𝑢(𝑥,𝑡):

𝜕𝑢/𝜕𝑡+𝑐*𝜕𝑢/𝜕𝑥=0,𝑐=𝑐𝑜𝑛𝑠𝑡. (1)

Физический смысл величины 𝑢 может быть различным. Например, это может быть давление в звуковой волне или электрический сигнал.

Физический смысл уравнения (1) заключается в следующем. В начальный момент времени (𝑡=0) функция 𝑢(𝑥,0) имеет некоторый профиль 𝑔(𝑥), т.е. это начальное условие задачи:

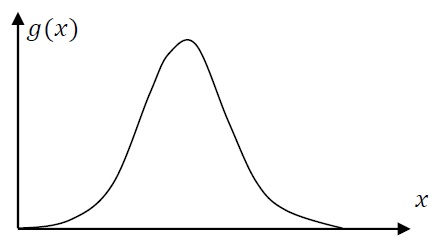
Точное решение уравнения дается выражением 𝑢(𝑥,𝑡)=𝑔(𝑥−𝑐𝑡), т.е. решение представляет собой ту же начальную функцию 𝑔(𝑥), но смещенную относительно начального положения на расстояние 𝑐𝑡:

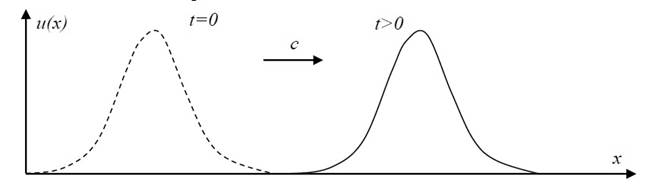
Таким образом, уравнение (1) описывает перемещение начального профиля 𝑔(𝑥) вправо по направлению оси 𝑥 со скоростью 𝑐. Поэтому уравнение называется уравнением переноса.

Применение МКР для решения уравнения переноса

Первым шагом для применения МКР является введение разностной сетки, показанной на рисунке:

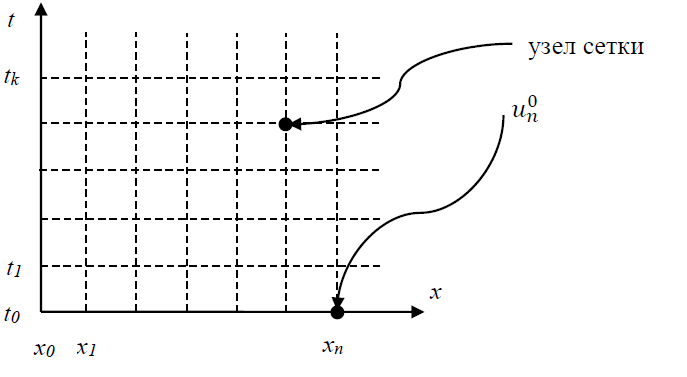
Сетка может быть равномерной (шаги сетки одинаковые) и неравномерной (шаги сетки различны).

Вторым шагом является аппроксимация уравнения на разностной сетке. Это можно сделать различными способами. В зависимости от выбранного способа полученное численное решение может лучше или хуже совпадать с аналитическим (или вообще не совпадать).

Введем обозначение:

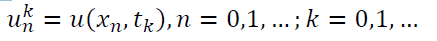
Индекс 𝑘 относится ко времени, индекс 𝑛 – к координате.

Это называется сеточной функцией. Очевидно, что эта функция дискретна, т.к. область ее значений – точки в узлах сетки.

Производные на сетке можно аппроксимировать так (№1):

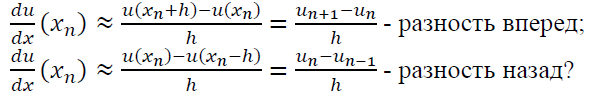
где h – шаг по координате.

Аналогично поступают с производными по времени, где τ – шаг по времени.

Тогда разностную схему для уравнения переноса можно записать следующим образом:

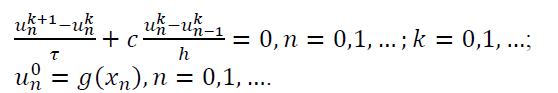
Из этой разностной схемы легко выразить значение 𝑢 на 𝑘+1 слое по времени:

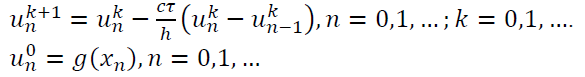
И таким образом вычислить решение итеративно. Поэтому такая схема называется явной.

С другой стороны, можно аппроксимироватьпроизводные иначеи получить другую разностную схему (№2):

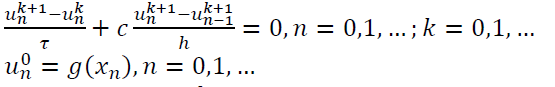
Она содержит значения 𝑢 на 𝑘+1 слое в трех местах, поэтому отсюда его явно выразить нельзя. В результате приходится записывать сразу все уравнения на всей разностной сетке и решать систему уравнений на каждом шаге по времени. Здесь используются методы, рассмотренные нами ранее для решения уравнений и систем уравнений.

Наконец, можно рассмотреть и такую схему (№3):

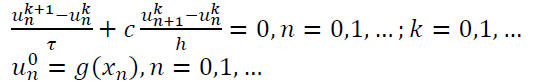
Откуда можно выразить 𝑢_𝑛^𝑘+1.

Метод конечных объемов

Метод конечных объемов подобен методу конечных разностей

Метод конечных элементов

На заре своего существования метод конечных элементов (МКЭ) применялся главным образом в строительной механике. Словосочетание конечный элемент появилось впервые применительно к анализу напряжений в плоскостях. Многие коммерческие пакеты, основанные на методе конечных элементов, изначально предназначались для решения строительных задач. Однако вскоре стало ясно, что методы конечных элементов имеют более широкую область применения: задачи теплопереноса, распределения электростатического потенциала, механики жидкостей, вибрационного анализа и многие другие. С ростом вычислительных возможностей компьютеров расширился диапазон и возросла сложность задач, доступных решению методом конечных элементов. пакеты, основанные на методе конечных элементов, изначально предназначались для решения строительных задач. Однако вскоре стало ясно, что методы конечных элементов имеют более широкую область применения: задачи теплопереноса, распределения электростатического потенциала, механики жидкостей, вибрационного анализа и многие другие. С ростом вычислительных возможностей компьютеров расширился диапазон и возросла сложность задач, доступных решению методом конечных элементов.

Метод конечных элементов (МКЭ, Finite Elements Method, FEM)– это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Идея МКЭ состоит в том, что любую непрерывную величину (температуру, давление, перемещение, др.) можно аппроксимировать дискретной моделью, которая строится из кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений исследуемой непрерывной величины в конечном числе точек рассматриваемой области.

Аппроксимирующие (кусочно-непрерывные) функции чаще всего выбираются в виде линейных, квадратичных или кубических полиномов. Полином, связанный с данным элементом, называется функцией элемента.

Рассмотрим применение МКЭ чуть подробней. В общем случае исследуемая непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. Итак, при построении дискретной модели непрерывной величины поступают следующим образом:

1. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.

2. Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

3. Область определения непрерывной величины разбивается на конечное число подобластей, которые и называются элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

4. Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента. Основная идея МКЭ наглядно показана на одномерном примере заданного распределения температуры в стержне рис. 1

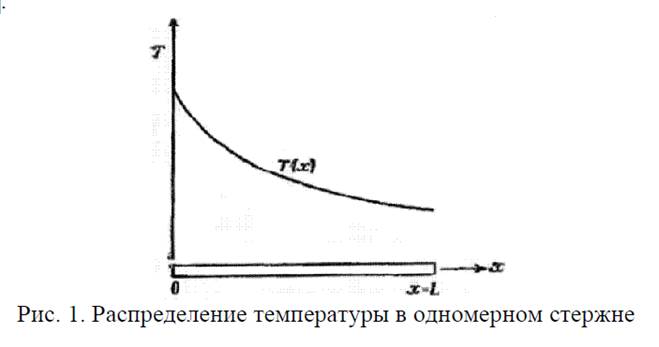
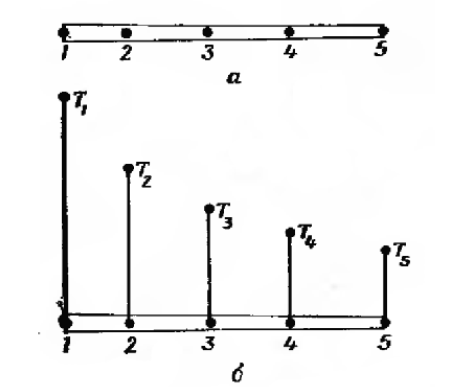
Рассматривается непрерывная величина T(x), область определения которой – отрезок OL вдоль оси х. Фиксированы и пронумерованы пять точек на оси x (рис. 2, а). Это узловые точки. Совсем не обязательно располагать узловые точки на равном расстоянии друг от друга. Очевидно, можно ввести в рассмотрение и более пяти точек, но этих пяти вполне достаточно, чтобы проиллюстрировать основную идею метода. Значения T(x) в данном случае известны в каждой узловой точке. Эти фиксированные значения представлены графически на рис. 2, б и обозначены в соответствии с номерами узловых точек через T₁, T₂, T₃, T₄, T₅.

Разбиение области на элементы может быть проведено двумя различными способами. Можно, например, ограничить каждый элемент двумя соседними узловыми точками, образовав четыре элемента (рис. 3, а), или разбить область на два элемента, каждый из которых содержит три узла (рис.3, б). Соответствующий элементу полином определяется по значениям Т(х) в узловых точках элемента. В случае разбиения области на четыре элемента, когда на каждый элемент приходится по два узла, функция элемента будет линейна по х (две точки однозначно определяют прямую линию).

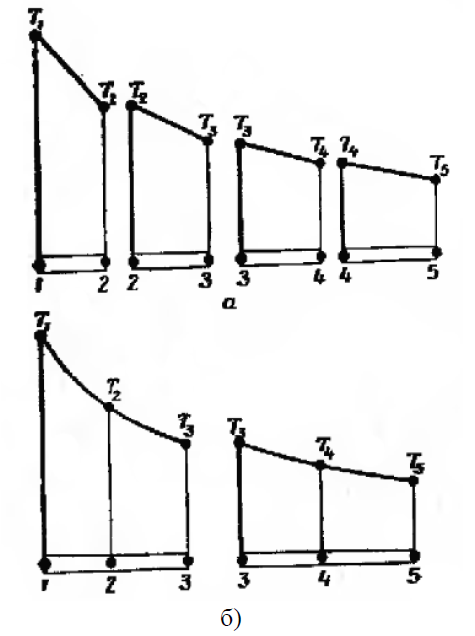
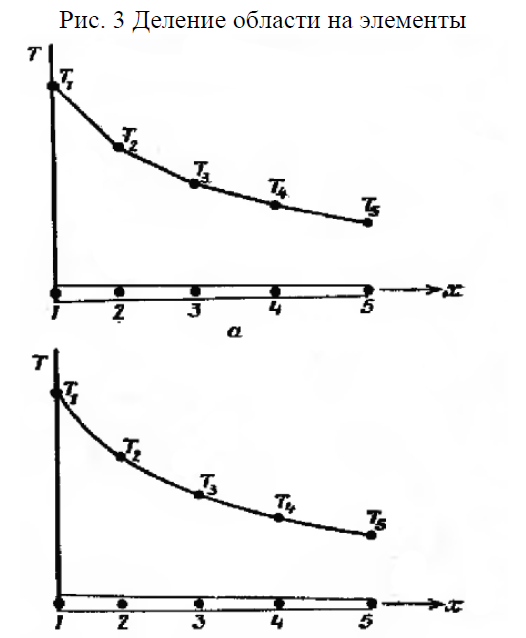
Окончательная аппроксимация Т(х) будет состоять из четырех кусочно-линейных функций, каждая из которых определена на отдельном элементе (рис. 4).

Другой способ разбиения области на два элемента с тремя узловыми точкам приводит к представлению функции элемента в виде полинома второй степени. В этом случае окончательной аппроксимацией Т(х) будет совокупность двух кусочно-непрерывных квадратичных функций. Это приближение будет именно кусочно-непрерывным, так как углы наклона графиков обеих этих функций могут иметь разные значения в третьем узле.

В общем случае распределение температуры неизвестно и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Снова определяются множество узлов и значения температуры в этих узлах T1, T2, T3, которые теперь являются переменными, так как они заранее неизвестны. Область разбивается на элементы, на каждом из которых определяется соответствующая функция элемента. Узловые значения Т(х) должны быть теперь «отрегулированы» таким образом, чтобы обеспечивалось «наилучшее» приближение к истинному распределению температуры. Это «регулирование» осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи. Если рассматривается задача распространения тепла, то минимизируется функционал, связанный с соответствующим дифференциальным уравнением. Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значений Т(х).