Основы специальной теории относительности

Относительность промежутков времени

Цель работы: изучение специальной теории относительности, моделей.

Краткая теория

Специальная (или частная) теория относительности (СТО) представляет собой современную физическую теорию пространства и времени. Наряду с квантовой механикой, СТО служит теоретической базой современной физики и техники. СТО часто называют релятивистской теорией, а специфические явления, описываемые этой теорией, – релятивистскими эффектами. Эти эффекты наиболее отчетливо проявляются при скоростях движения тел, близких к скорости света в вакууме c ≈ 3·10⁸ м/с. Специальная теория относительности была создана А. Эйнштейном (1905 г.). Предшественниками Эйнштейна, очень близко подошедшими к решению проблемы, были нидерландский физик Х. Лоренц и выдающийся французский физик А. Пуанкаре.

Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (υ << c). В нерелятивистской физике принималось как очевидный факт существование единого мирового времени t, одинакового во всех системах отсчета. В основе классической механики лежит механический принцип относительности (или принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета. Этот принцип означает, что законы динамики инвариантны (т. е. неизменны) относительно преобразований Галилея, которые позволяют вычислить координаты движущегося тела в одной инерциальной системе (K), если заданы координаты этого тела в другой инерциальной системе (K'). В частном случае, когда система K' движется со скоростью υ вдоль положительного направления оси x системы K (рис. 1.1), преобразования Галилея имеют вид:

		x = x' + υt, y = y', z = z', t = t'.	(1.1)
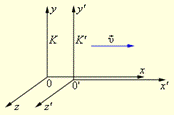Рис. 1.1. Две инерциальные системы отсчета K и K'.	Предполагается, что в начальный момент оси координат обеих систем совпадают. Из преобразований Галилея следует классический закон преобразования скоростей при переходе от одной системы отсчета к другой: ux = u'x + υ, uy = u'y, uz = u'z. (1.2)

Ускорения тела во всех инерциальных системах оказываются одинаковыми:

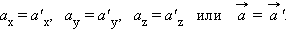(1.3)

Следовательно, уравнение движения классической механики (второй закон Ньютона) 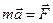не меняет своего вида при переходе от одной инерциальной системы к другой.

К концу XIX века начали накапливаться опытные факты, которые вступили в противоречие с законами классической механики. Большие затруднения возникли при попытках применить механику Ньютона к объяснению распространения света. Предположение о том, что свет распространяется в особой среде – эфире, было опровергнуто многочисленными экспериментами. А. Майкельсон в 1881 году, а затем в 1887 году совместно с Э. Морли (оба – американские физики) пытался обнаружить движение Земли относительно эфира («эфирный ветер») с помощью интерференционного опыта. Упрощенная схема опыта Майкельсона–Морли представлена на рис.1.2.

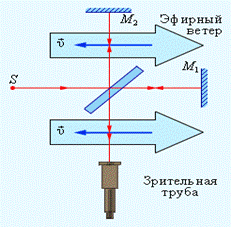Рис. 1.2. Упрощенная схема интерференционного опыта Майкельсона–Морли. 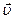– орбитальная скорость Земли.

В этом опыте одно из плеч интерферометра Майкельсона устанавливалось параллельно направлению орбитальной скорости Земли (υ = 30 км/с). Затем прибор поворачивался на 90°, и второе плечо оказывалось ориентированным по направлению орбитальной скорости. Расчеты показывали, что если бы неподвижный эфир существовал, то при повороте прибора интерференционные полосы должны были сместиться на расстояние, пропорциональное (υ / c)2. Опыт Майкельсона–Морли, неоднократно повторенный впоследствии со все более возрастающей точностью, дал

отрицательный результат. Анализ результатов опыта Майкельсона–Морли и ряда других экспериментов позволил сделать вывод о том, что представления об эфире как среде, в которой распространяются световые волны, ошибочно. Следовательно, для света не существует избранной (абсолютной) системы отсчета. Движение Земли по орбите не оказывает влияния на оптические явления на Земле.

Исключительную роль в развитии представлений о пространстве и времени сыграла теория Максвелла. К началу XX века эта теория стала общепризнанной. Предсказанные теорией Максвелла электромагнитные волны, распространяющиеся с конечной скоростью, уже нашли практическое применение – в 1895 году было изобретено радио (А. С. Попов). Но из теории Максвелла следовало, что скорость распространения электромагнитных волн в любой инерциальной системе отсчета имеет одно и то же значение, равное скорости света в вакууме. Отсюда следует, что уравнения, описывающие распространение электромагнитных волн, не инвариантны относительно преобразований Галилея. Если электромагнитная волна (в частности, свет) распространяется в системе отсчета K' (рис. 1.1) в положительном направлении оси x', то в системе K свет должен, согласно галилеевской кинематике распространяться со скоростью c + υ, а не c.

Итак, на рубеже XIX и XX веков физика переживала глубокий кризис. Выход был найден Эйнштейном ценой отказа от классических представлений о пространстве и времени. Наиболее важным шагом на этом пути явился пересмотр используемого в классической физике понятия абсолютного времени. Классические представления, кажущиеся наглядными и очевидными, в действительности оказались несостоятельными. Многие понятия и величины, которые в нерелятивистской физике считались абсолютными, т. е. не зависящими от системы отсчета, в эйнштейновской теории относительности переведены в разряд относительных.

Так как все физические явления происходят в пространстве и во времени, новая концепция пространственно-временных закономерностей не могла не затронуть в итоге всю физику.

В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г.

1. Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.

2. Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

Эти принципы следует рассматривать как обобщение всей совокупности опытных фактов. Следствия из теории, созданной на основе этих принципов, подтверждались бесконечными опытными проверками. СТО позволила разрешить все проблемы «доэйнштейновской» физики и объяснить «противоречивые» результаты известных к тому времени экспериментов в области электродинамики и оптики. В последующее время СТО была подкреплена экспериментальными данными, полученными при изучении движения быстрых частиц в ускорителях, атомных процессов, ядерных реакций и т. п.

Постулаты СТО находятся в явном противоречии с классическими представлениями. Рассмотрим такой мысленный эксперимент: в момент времени t = 0, когда координатные оси двух инерциальных систем K и K' совпадают, в общем начале координат произошла кратковременная вспышка света. За время t системы сместятся относительно друг друга на расстояние υt, а сферический волновой фронт в каждой системе будет иметь радиус ct (рис. 1.3), так как системы равноправны и в каждой из них скорость света равна c.

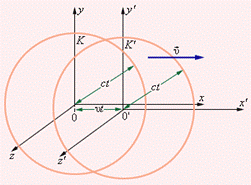Рис. 1.3. Кажущееся противоречие постулатов СТО.

С точки зрения наблюдателя в системе K центр сферы находится в точке O, а с точки зрения наблюдателя в системе K' он будет находиться в точке O'. Следовательно, центр сферического фронта одновременно находится в двух разных точках! Причина возникающего недоразумения лежит не в противоречии между двумя принципами СТО, а в допущении, что положение фронтов сферических волн для обеих систем

относится к одному и тому же моменту времени.

Это допущение заключено в формулах преобразования Галилея, согласно которым время в обеих системах течет одинаково: t = t'. Следовательно, постулаты Эйнштейна находятся в противоречии не друг с другом, а с формулами преобразования Галилея. Поэтому на смену галилеевых преобразований СТО предложила другие формулы преобразования при переходе из одной инерциальной системы в другую – так называемые преобразования Лоренца, которые при скоростях движения, близких к скорости света, позволяют объяснить все релятивисткие эффекты, а при малых скоростях (υ << c) переходят в формулы преобразования Галилея. Таким образом, новая теория (СТО) не отвергла старую классическую механику Ньютона, а только уточнила пределы ее применимости. Такая взаимосвязь между старой и новой, более общей теорией, включающей старую теорию как предельный случай, носит название принципа соответствия.

При выполнении любых физических измерений исключительную роль играют пространственно-временные соотношения между событиями. В СТО событие определяется как физическое явление, происходящее в какой-либо точке пространства в некоторый момент времени в избранной системе отсчета. Таким образом, чтобы полностью охарактеризовать событие, требуется не только выяснить его физическое содержание, но и определить его место и время. Для этого необходимо использовать процедуры измерения расстояний и промежутков времени. Эйнштейн показал, что эти процедуры нуждаются в строгом определении.

Для того чтобы в выбранной системе отсчета выполнять измерения промежутка времени между двумя событиями (например, началом и концом какого-либо процесса), происходящими в одной и той же точке пространства, достаточно иметь эталонные часы. Наибольшей точностью в настоящее время обладают часы, основанные на использовании собственных колебаний молекул аммиака (молекулярные часы) или атомов цезия (атомные часы). Измерение промежутка времени опирается на понятие одновременности: длительность какого-либо процесса определяется путем сравнения с промежутком времени, отделяющим показание часов, одновременное с концом процесса, от показания тех же часов, одновременного с началом процесса. Если же оба события происходят в разных точках системы отсчета, то для измерения промежутков времени между ними в этих точках необходимо иметь синхронизованные часы.

Эйнштейновское определение процедуры синхронизации часов основано на независимости скорости света в пустоте от направления распространения. Пусть из точки A в момент времени t₁ по часам A отправляется короткий световой импульс (рис. 1.4). Пусть время прихода импульса в B и отражения его назад на часах B есть t'. Наконец, пусть отраженный сигнал возвращается в A в момент t₂ по часам A. Тогда по определению часы в A и B идут синхронно, если t' = (t₁ + t₂) / 2.

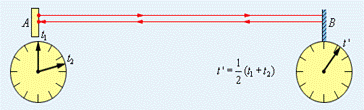Рис. 1.4. Синхронизация часов в СТО.

Существование единого мирового времени, не зависящего от системы отсчета, которое принималось как очевидный факт в классической физике, эквивалентно неявному допущению о возможности

синхронизации часов с помощью сигнала, распространяющегося с бесконечно большой скоростью.

Итак, в разных точках выбранной системы отсчета можно расположить синхронизованные часы. Теперь можно дать определение понятия одновременности событий, происходящих в пространственно-разобщенных точках: эти события одновременны, если синхронизованные часы показывают одинаковое время.

Рассмотрим теперь вторую инерциальную систему K', которая движется с некоторой скоростью υ в положительном направлении оси x системы K. В разных точках этой новой системы отсчета также можно расположить часы и синхронизировать их между собой, используя описанную выше процедуру. Теперь интервал времени между двумя событиями можно измерять как по часам в системе K, так и по часам в системе K'. Будут ли эти интервалы одинаковы? Ответ на этот вопрос должен находиться в согласии с постулатами СТО.

Пусть оба события в системе K' происходят в одной и той же точке и промежуток времени между ними равен τ₀ по часам системы K'. Этот промежуток времени называется собственным временем. Каким будет промежуток времени между этими же событиями, если его измерить по часам системы K?

Для ответа на этот вопрос рассмотрим следующий мысленный эксперимент. На одном конце твердого стержня некоторой длины l расположена импульсная лампа B, а на другом конце – отражающее зеркало M. Стержень расположен, неподвижно в системе K' и ориентирован параллельно оси y' (рис. 1.5). Событие 1 – вспышка лампы, событие 2 – возвращение короткого светового импульса к лампе.

В системе K' оба рассматриваемых события происходят в одной и той же точке. В системе K' оба рассматриваемых события происходят в одной и той же точке.

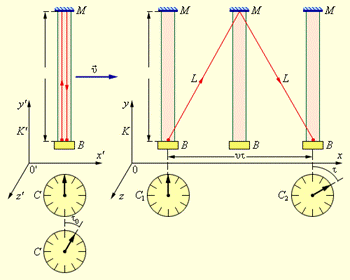Рис. 1.5. Относительность промежутков времени. Моменты наступлений событий в системе K' фиксируются по одним и тем же часам C, а в системе K – по двум синхронизованным пространственно-разнесенным часам C1 и C2. Система K' движется со скоростью υ в положительном направлении оси x системы K.

Промежуток времени между ними (собственное время) равен τ = 2l / c. С точки зрения наблюдателя, находящегося в системе K, световой импульс движется между зеркалами зигзагообразно и проходит путь 2L, равный 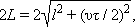где τ – промежуток времени между отправлением светового импульса и его возвращением, измеренный по синхронизованным часам C1 и C2, расположенными в разных точках системы K. Но согласно второму постулату СТО, световой импульс двигался в системе K с той же скоростью c, что и в системе K'. Следовательно, τ = 2L / c.

Из этих соотношений можно найти связь между τ и τ₀:

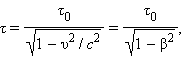(1.4)

где β = υ / c.

Таким образом, промежуток времени между двумя событиями зависит от системы отсчета, т. е. является относительным. Собственное время τ₀ всегда меньше, чем промежуток времени между этими же событиями, измеренный в любой другой системе отсчета. Этот эффект называют релятивистским замедлением времени. Замедление времени является следствием инвариантности скорости света.

Эффект замедления времени является взаимным, в согласии с постулатом о равноправии инерциальных систем K и K': для любого наблюдателя в K или K' медленнее идут часы, связанные с движущейся по отношению к наблюдателю системой. Этот вывод СТО находит непосредственное опытное подтверждение. Например, при исследовании космических лучей в их составе обнаружены μ-мезоны – элементарные частицы с массой, примерно в 200 раз превышающей массу электрона. Эти частицы нестабильны, их среднее собственное время жизни равно τ₀ = 2,2·10^–6 с. Но в космических лучах μ-мезоны движутся со скоростью, близкой к скорости света. Без учета релятивистского эффекта замедления времени они в среднем пролетали бы в атмосфере путь, равный cτ₀ ≈ 660 м. На самом деле, как показывает опыт, мезоны за время жизни успевают пролетать без распада гораздо большие расстояния. Согласно СТО, среднее время жизни мезонов по часам земного наблюдателя равно 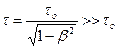, так как β = υ / c близко к единице. Поэтому средний путь υτ, проходимый мезоном в земной системе отсчета, оказывается значительно больше 660 м.

С релятивистским эффектом замедления времени связан так называемый «парадокс близнецов». Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.

Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.

Эффекты замедления времени пренебрежимо малы, если скорость космического корабля гораздо меньше скорости света c. Тем не менее, удалось получить прямое подтверждение этого эффекта в экспериментах с макроскопическими часами. Наиболее точные часы – это атомные часы на пучке атомов цезия. Эти часы «тикают» 9192631770 раз в секунду. Американские физики в 1971 году провели сравнение двух таких часов, причем одни из них находились в полете вокруг Земли на обычных реактивных лайнерах, а другие оставались на Земле в военно-морской обсерватории США. В соответствии с предсказаниями СТО, путешествующие на лайнерах часы должны были отстать от находящихся на Земле часов на (184 ± 23)·10^–9 с. Наблюдаемое отставание составило (203 ± 10)·10^–9 с, т. е. в пределах ошибок измерений. Через несколько лет эксперимент был повторен и дал результат, согласующийся со СТО с точностью 1 %.

В настоящее время уже необходимо принимать во внимание релятивистский эффект замедления хода часов при транспортировке атомных часов на большие расстояния.

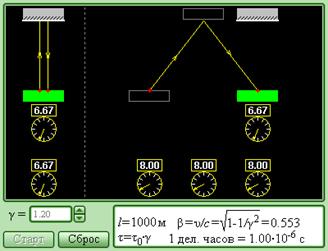Изучите модель «Относительность промежутков времени».

Модель. Относительность промежутков времени.	Относительность промежутков времени – одно из важных следствий специальной теории относительности Эйнштейна. Интервал времени между двумя событиями может быть разным в разных системах отсчета. Если два события происходят в одной и той же точке пространства в некоторой системе отсчета, и интервал времени, измеренный по часам неподвижного наблюдателя, оказался равным τ0, то для наблюдателя в другой системе, которая движется относительно первой с постоянной скоростью υ, интервал времени между двумя этими событиями будет равен τ:

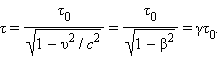Здесь c – скорость света, β = υ / c.Интервал τ всегда больше интервала τ₀, который называется собственным временем. Это означает, в частности, что ход часов, движущихся относительно наблюдателя, замедляется. Этот вывод теории относительности вытекает из постулата о постоянстве скорости света в различных системах отсчета.

Компьютерная модель позволяет познакомиться с одним из важных следствий специальной теории относительности Эйнштейна - относительностью промежутков времени. На экране дисплея представлен эксперимент по измерению интервала времени между двумя событиями наблюдателями в различных системах отсчета. Результаты измерения собственного времени и времени по часам движущегося наблюдателя выводятся на экран дисплея.

В левой части экрана воспроизводится эксперимент по измерению времени распространения светового импульса туда и обратно на неподвижной базеl = 1 км. Событие 1 – (световая вспышка) и событие 2 – (возвращение светового импульса) происходят в одной точке системы отсчета. Поэтому часы измеряют собственное времяτ₀ = 2l / c. В правой части этот эксперимент рассматривается с точки зрения наблюдателя, который движется с некоторой скоростью υ перпендикулярно базе. События 1 и 2 в системе отсчета этого наблюдателя происходят в пространственно разобщенных точках. Время τ = 2L / c, измеренное по синхронизованным часам этой системы, окажется больше собственного времени τ₀.

В компьютерной модели можно изменять величину γ, которая связана со скоростью υ соотношением

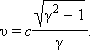При нажатии кнопки «Сброс» на часах в обеих системах отсчета высвечивается время наступления событий 1и 2.

Пусть твердый стержень покоится в системе отсчета K', движущейся со скоростью υ относительно системы отсчета K (рис. 1.6). Стержень ориентирован параллельно оси x'. Его длина, измеренная с помощью эталонной линейки в системе K', равна l₀. Ее называют собственной длиной. Какой будет длина этого стержня, измеренная наблюдателем в системе K? Для ответа на этот вопрос необходимо дать определения процедуры измерения длины дв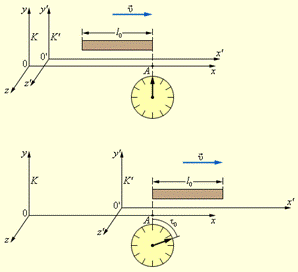ижущегося стержня.

Рис. 1.6. Измерение длины движущегося стержня.

Под длиной l стержня в системе K, относительно которой стержень движется, понимают расстояние между координатами концов стержня, зафиксированными одновременно по часам этой системы. Если известна скорость системы K' относительно K, то измерение длины движущегося стержня можно свести к измерению времени: длина l движущегося со скоростью υ стержня равна произведению υτ0, где τ0 – интервал времени по часам в системе K между прохождением начала стержня и его конца мимо какой-нибудь

неподвижной точки (например, точки A) в системе K (рис. 1.6). Поскольку в системе K оба события (прохождение начала и конца стержня мимо фиксированной точки A) происходят в одной точке, то промежуток времени τ₀ в системе K является собственным временем. Итак, длина l движущегося стержня равна l = υτ₀.

Найдем теперь связь между l и l₀. С точки зрения наблюдателя в системе K', точка A, принадлежащая системе K, движется вдоль неподвижного стержня налево со скоростью υ, поэтому можно записать

l0 = υτ,

(1.5)

где τ есть промежуток времени между моментами прохождения точки A мимо концов стержня, измеренный по синхронизованным часам в K'. Используя связь между промежутками времени τ и τ₀ 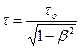, найдем

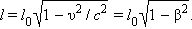(1.6)

Таким образом, длина стержня зависит от системы отсчета, в которой она измеряется, т. е. является относительной величиной. Длина стержня оказывается наибольшей в той системе отсчета, в которой стержень покоится. Движущиеся относительно наблюдателя тела сокращаются в направлении своего движения. Этот релятивистский эффект носит название лоренцева сокращения длины.

Расстояние не является абсолютной величиной, оно зависит от скорости движения тела относительно данной системы отсчета. Сокращение длины не связанно с какими-либо процессами, происходящими в самих телах. Лоренцево сокращение характеризует изменение размера движущегося тела в направлении его движения. Если стержень на рис. 1.6 расположить перпендикулярно оси x, вдоль которой движется система K', то длина стержня оказывается одинаковой для наблюдателей в обеих системах K и K'. Это утверждение находится в соответствии с постулатом о равноправии всех инерциальных систем. Для доказательства можно рассмотреть следующий мысленный эксперимент. Расположим в системах K и K' вдоль осей y и y' два жестких стержня. Стержни имеют одинаковые собственные длины l, измеренные неподвижными по отношению к каждому из стержней наблюдателями в K и K', и один из концов каждого стержня совпадает с началом координат O или O'. В некоторый момент стержни оказываются рядом и представляется возможность сравнить их непосредственно: конец каждого стержня может сделать метку на другом стержне. Если бы эти метки не совпали с концами стержней, то один из них оказался бы длиннее другого с точки зрения обеих систем отсчета. Это противоречило бы принципу относительности.

Следует обратить внимание, что при малых скоростях движения (υ << c) формулы СТО переходят в классические соотношения: l ≈ l₀ и τ ≈ τ₀. Таким образом, классические представления, лежащие в основе механики Ньютона и сформировавшиеся на основе многовекового опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при β = υ / c → 0. В этом проявляется принцип соответствия.

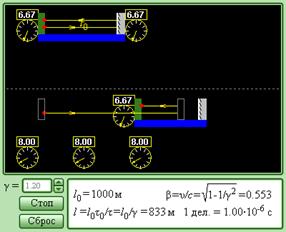Изучите модель «Относительность длины».

Модель. Относительность длины.	Одним из важных следствий специальной теории относительности является вывод об относительности расстояний. Расстояние не является абсолютной величиной, а зависит от скорости движения тела относительно данной системы отсчета. Пусть длина твердого стержня, измеренная в собственной системе отсчета, в которой стержень неподвижен, равна l0. Под длиной l стержня в другой системе отсчета, относительно которой стержень движется с некоторой скоростью υ, понимают расстояние между концами стержня, зафиксированными одновременно по часам этой системы. Тогда согласно теории относительности имеет место соотношение:

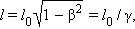где

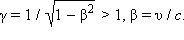
Таким образом, длина движущегося стержня оказывается всегда меньше длины покоящегося стержня.

Относительность расстояний (длин) связана с постоянством скорости света во всех инерциальных системах и с относительностью промежутков времени.

Компьютерная программа моделирует эксперимент по измерению длины твердого стержня двумя наблюдателями, находящимися в различных инерциальных системах. Один из наблюдателей неподвижен по отношению к стержню, другой движется с некоторой скоростью υ вдоль стержня. Эксперимент состоит в измерении времени распространения светового импульса от одного конца стержня до другого и обратно. Событие 1 – короткая световая вспышка на одном конце стержня событие 2 – возвращение светового импульса к лампе! В собственной системе отсчета интервал времени между этими событиями равен τ₀ = 2l₀ / c. В движущейся системе отсчета интервал времени между этими событиями равен

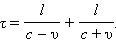Из этих соотношений следует

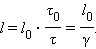В компьютерном эксперименте можно изменять относительную скорость систем отсчета. В верхней части экрана воспроизводится эксперимент по измерению собственного времениτ₀ между событиями в системе, в которой стержень неподвижен. В нижней части экрана этот же эксперимент выполняет наблюдатель в движущейся по отношению к стержню системе отсчета. Результаты измерений промежутков времени τ₀ и τ высвечиваются на часах в обеих системах отсчета.

Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены другими преобразованиями. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x', y', z') и моментом времени t' этого же события, наблюдаемого в системе отсчета K'.

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

K' → K K → K' 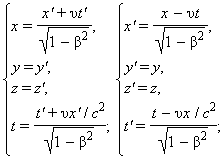β = υ / c.

(1.7)

Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x' системы K' происходит процесс длительностью τ₀ = t'₂ – t'₁ (собственное время), где t'₁ и t'₂ – показания часов в K' в начале и конце процесса. Длительность τ этого процесса в системе K будет равна

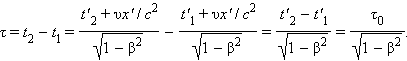(1.8)

Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K' (x'₁ ≠ x'₂) одновременно с точки зрения наблюдателя в K' (t'₁ = t'₂ = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь

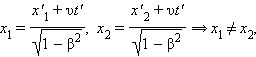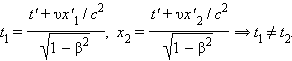(1.9)

Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t₂ – t₁ определяется знаком выражения υ(x'₂ – x'₁), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.

Относительность одновременности пространственно-разобщенных событий можно проиллюстрировать на следующем примере.

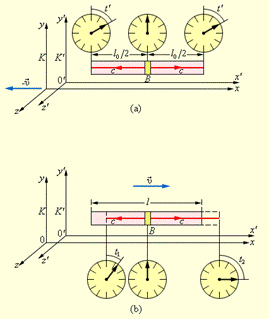Рис. 1.7. Относительность одновременности. Световой импульс достигает концов твердого стержня одновременно в системе отсчета K' (a) и не одновременно в системе отсчета K (b).

Пусть в системе отсчета K' вдоль оси x' неподвижно расположен длинный жесткий стержень. В центре стержня находится импульсная лампа B, а на его концах установлены двое синхронизованных часов (рис. 1.7(a)), система K' движется вдоль оси x системы K со скоростью υ. В некоторый момент времени лампа посылает короткие световые импульсы в направлении концов стержня. В силу равноправия обоих направлений свет в системе K' дойдет до концов стержня одновременно, и часы, закрепленные на концах стержня, покажут одно и то же время t'. Относительно системы K концы стержня движутся со скоростью υ так, что один конец движется навстречу световому импульсу, а другой конец свету приходится догонять. Так как скорости распространения световых импульсов в обоих

направлениях одинаковы и равны c, то, с точки зрения наблюдателя в системе K, свет раньше дойдет до левого конца стержня, чем до правого (рис. 1.7(b)).

Преобразования Лоренца выражают относительный характер промежутков времени и расстояний. Однако, в СТО наряду с утверждением относительного характера пространства и времени важную роль играет установление инвариантных физических величин, которые не изменяются при переходе от одной системе отсчета к другой. Одной из таких величин является скорость света c в вакууме, которая в СТО приобретает абсолютный характер. Другой важной инвариантной величиной, отражающей абсолютный характер пространственно-временных связей, является интервал между событиями.

Пространственно-временной интервал определяется в СТО следующим соотношением:

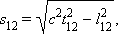(1.10)

где t₁₂ – промежуток времени между событиями в некоторой системе отсчета, а l₁₂ – расстояние между точками, в которых происходят рассматриваемые события, в той же системе отсчета. В частном случае, когда одно из событий происходит в начале координат (x₁ = y₁ = z₁ = 0) системы отсчета в момент времени t₁ = 0, а второе – в точке с координатами x, y, z в момент времени t, пространственно-временной интервал между этими событиями записывается в виде

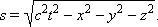(1.11)

С помощью преобразований Лоренца можно доказать, что пространственно-временной интервал между двумя событиями не изменяется при переходе из одной инерциальной системы в другую. Инвариантность интервала означает, что, несмотря на относительность расстояний и промежутков времени, протекание физических процессов носит объективный характер и не зависит от системы отсчета.

Если одно из событий представляет собой вспышку света в начале координат системы отсчета при t = 0, а второе – приход светового фронта в точку с координатами x, y, z в момент времени t (рис. 1.3), то

x2 + y2 + z2 = c2t2,

(1.12)

и, следовательно, интервал для этой пары событий s = 0. В другой системе отсчета координаты и время второго события будут другими, но и в этой системе пространственно-временной интервал s' окажется равным нулю, так как

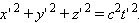(1.13)

Для любых двух событий, связанных между собой световым сигналом, интервал равен нулю.

Из преобразований Лоренца для координат и времени можно получить релятивистский закон сложения скоростей. Пусть, например, в системе отсчета K' вдоль оси x' движется частица со скоростью 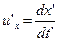. Составляющие скорости частицы u'_x и u'_z равны нулю. Скорость этой частицы в системе K будет равна .

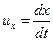С помощью операции дифференцирования из формул преобразований Лоренца можно найти:

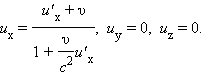(1.14)

Эти соотношения выражают релятивистский закон сложения скоростей для случая, когда частица движется параллельно относительной скорости 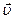систем отсчета K и K'.

При υ << c релятивистские формулы переходят в формулы классической механики: