Сокращенная и тупиковая ДНФ (КНФ)

В совершенной ДНФ каждая единица ФАЛ представляется соответствующей конституентой единицы, являющейся конъюнкцией всех переменных функции. Количество конституент единицы, входящих в СДНФ, равно числу наборов, на которых ФАЛ равна единице.

В отличие от СДНФ в сокращенную ДНФ включают элементарные конъюнкции, которые получаются в результате проведения операции склеивания конституент единицы, входящих в заданную ФАЛ. Такие элементарные конъюнкции заменяют в заданной ФАЛ несколько конституент единицы.

Функцию j, входящую в заданную функцию f, называют ее импликантой.

Вхождение одной функции в другую можно определить с помощью понятия накрытия.

Пусть на каком-либо наборе переменных функция f равна а₁, а функция j на том же наборе равна а₂. Тогда говорят, что на данном наборе функция f своим значением а₁ накрывает значение а₂ функции j.

Функция j входит в функцию f, если все единицы функции j накрываются единицами функции f, а нули функции j могут быть накрыты как нулями, так и единицами функции f. Функцию j, входящую в данную функцию f, называют импликантой функции f.

Простой импликантой функции f называется элементарная конъюнкция, входящая в данную функцию и из которой не может быть получена другая конъюнкция, входящая в эту функцию, исключением из первой какой-либо переменной. Простые импликанты, входящие в заданную ФАЛ, представляют собой элементарные конъюнкции, содержащие наименьшее число переменных, т.е. элементарные конъюнкции наименьшего ранга.

Любая ФАЛ имеет конечное число простых импликант, но не более числа конституент единицы в СДНФ этой функции. Так как простые импликанты – это элементарные конъюнкции, в которые входят все конституенты единицы функции, то дизъюнкция всех простых импликант функции f(х_n, …, х₂, х₁) равна этой функции и называется сокращенной ДНФ.

Любая ФАЛ имеет единственную сокращенную ДНФ. По методу Квайна сокращенную ДНФ (КНФ) можно получить путем преобразования СДНФ (СКНФ) с помощью операций неполного склеивания и поглощения.

Если две элементарные конъюнкции/дизъюнкции( в том числе и конституенты единицы/нуля) одного и того же ранга и одних и тех же переменных отличаются только знаком отрицания одной из переменных 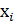, то они склеиваются по этой переменной:

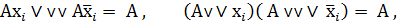
где А - элементарная конъюнкция/дизъюнкция.

Такие элементарные конъюнкции/дизъюнкции называются соседними.

Операции неполного склеивания определяются формулами:

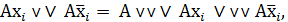
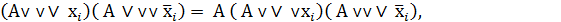(7)

т.е. в правой части равенств (7), кроме члена А, остаются обе склеивающиеся конъюнкции Ах_i и 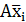или дизъюнкци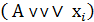и и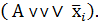

Согласно теореме Квайна, если в СДНФ (СКНФ) ФАЛ выполнить все операции неполного склеивания и затем все операции поглощения, то получится сокращенная ДНФ (КНФ) этой функции.

Одна и та же конституента единицы может склеиваться не с одной, а с несколькими конституентами единицы, в результате чего получаются различные простые импликанты. Поэтому для нахождения всех простых импликант функции выполняется операция неполного склеивания.

В общем случае сокращенная ДНФ не является минимальной, так как некоторые простые импликанты могут накрываться дизъюнкцией других импликант и эти простые импликанты можно исключить.

Дизъюнкция простых импликант, ни одну из которых нельзя исключить, называется тупиковой ДНФ заданной ФАЛ.

ФАЛ может иметь несколько тупиковых форм. Тупиковые формы, содержащие наименьшее количество букв, называются минимальными. Поэтому для нахождения минимальных форм нужно получить все тупиковые формы ФАЛ и из последних выбрать минимальные. Некоторые ФАЛ могут иметь несколько как тупиковых, так и минимальных форм.

Минимизация функций алгебры логики выполняется по методам Квайна, Квайна – Мак-Класки, по методу Квайна с применением карт Карно, по методу Квайна с применением карт Карно и преобразования Петрика и другими методами. Метод Квайна является основополагающим методом минимизации в классе ДНФ и КНФ ФАЛ. Однако трудоемкими этапами минимизации ФАЛ по методу Квайна являются нахождение простых и существенных (ядровых) импликант функций. Карты Карно позволяют существенно сократить количество сравнений конституент единицы и нуля для выявления склеивающихся конъюнкций. Преобразования Петрика позволяют после нахождения простых импликант, т.е. после нахождения сокращенной ДНФ, и существенных импликант найти аналитически все тупиковые и минимальные ДНФ и КНФ.

Для нахождения минимальных КНФ можно рекомендовать два метода:

1. Метод Квайна, в основу которого берется операция склеивания конституент нуля функции. Конституентам нуля на карте Карно соответствуют пустые клетки (или клетки, содержащие нули). Правила склеивания конституент нуля аналогичны правилам склеивания конституент единицы. Для нахождения простых и существенных дизъюнкций и тупиковых и минимальных КНФ можно использовать карты Карно и преобразование Петрика.

2. Минимизация функции, инверсной заданной, и преобразование полученной минимальной ДНФ функции 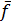по законам инверсии и де Моргана.