Передача теплоты через цилиндрическую стенку

Граничные условия первого рода.Теплопроводность однослойной стенки. Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d₁=2r₁ и наружным d₂=2r_2.

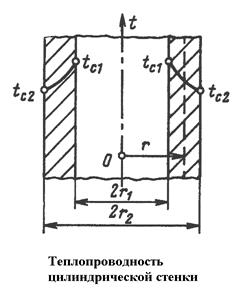На поверхностях стенки заданы постоянные температуры t_c1 и t_c2. В заданном интервале температур коэффициент теплопроводности материала стенки является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.

Дифференциальное уравнение теплопроводности в цилиндрической системе координат

.

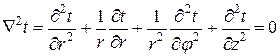При этом ось z совмещена с осью трубы. При заданных условиях температура изменяется только в радиальном направлении и температурное поле будет одномерным

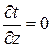и .

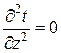Так как температуры на поверхностях неизменны и изотермические поверхности имеют с трубой общую ось, то температура не должна изменяться вдоль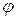

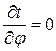и .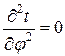

С учетом этого дифференциальное уравнение

.

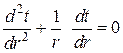Граничные условия: при r=r₁ t=t_c1;

r=r₂ t=t_c2.

После решения дифференциального уравнения получается уравнение температурного поля цилиндрической стенки

.

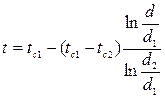Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, объясняется следующим образом. Для плоской стенки плотность теплового потока остается одинаковой для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянное значение. Для цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса.

Для нахождения количества теплоты, проходящего через цилиндрическую поверхность в единицу времени, воспользуемся законом Фурье

Q= .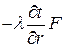

Подставляя в уравнение закона Фурье значение градиента температуры, и учитывая, что F=2 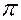rl

,

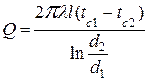где Q измеряется в Вт. Видно, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, не зависит от радиуса.

Тепловой поток может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом плотность теплового потока через единицу внутренней поверхности, Вт/м²

.

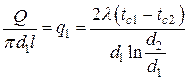Тепловой поток через единицу наружной поверхности, Вт/м²

.

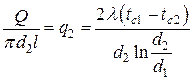Тепловой поток через единицу длины трубы, Вт/м

.

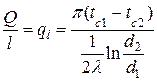Тепловой поток, отнесенный к единице длины трубы, называется линейной плотностью теплового потока. Плотности теплового потока q₁ и q₂ при передаче теплоты через трубы неодинаковы, причем всегда q₁ > q₂.

Связь между линейной плотностью теплового потока и внутренними и наружными поверхностными плотностями теплового потока q_l=πd₂q₂=πd₁q₁.

Граничные условия третьего рода (теплопередача).Теплопередача однослойной стенки.Рассмотрим однородную цилиндрическую стенку с постоянным коэффициентом теплопроводности 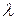. Заданы постоянные температуры подвижных сред t_ж1 и t_ж2 и постоянные значения коэффициента теплоотдачи на внутренней и наружной поверхностях трубы 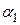и 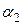. Необходимо найти t_c1; t_c2; q_l.

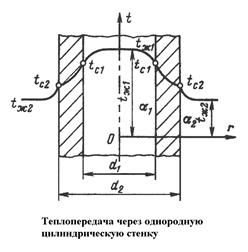Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями с торцов трубы можно пренебречь.

При установившемся тепловом режиме количество теплоты, отдаваемое от горячей жидкости цилиндрической стенке по закону Ньютона-Рихмана

.

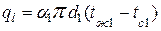Количество теплоты, передаваемое теплопроводностью через стенку

.

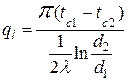Теплота, передаваемая от стенки к холодной жидкости

.

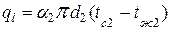Складывая уравнения, входящие в систему, получаем температурный напор

.

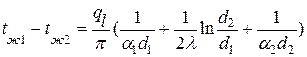Отсюда следует

.

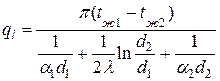Обозначим

.

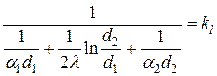С учетом этого уравнение теплопередачи

.

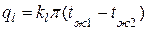Величина k_l называется линейным коэффициентом теплопередачи, Вт/(м∙К). Он характеризует интенсивность передачи теплоты от одной среды к другой через разделяющую стенку. Значение k_l численно равно количеству теплоты, которое проходит через стенку длиной 1 м в единицу времени от одной среды к другой при разности температур между ними в 1К.

Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи

.

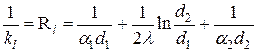Тепловой поток со всей поверхности трубы

.

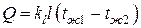Если тепловой поток через цилиндрическую стенку отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, Вт/м², отнесенную к единице соответствующей поверхности трубы

,

,

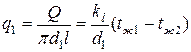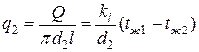где , .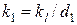

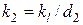Если толщина стенки цилиндра мала по сравнению с диаметром, т.е. 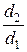<2, тогда для технических расчетов можно пользоваться формулой коэффициента теплопередачи для плоской стенки.

Теплопередача через многослойную стенку. При теплопередаче через многослойную цилиндрическую стенку система равенств должна быть заменена системой, учитывающей сопротивление теплопроводности всех слоев

.

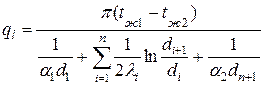Температуры на поверхностях многослойной стенки

,

,

.
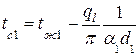
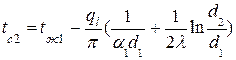
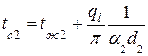