Оценка тесноты связи: коэффициент корреляции, индекс корреляции, коэффициенты эластичности и детерминации

Наряду с построением уравнения регрессии осуществляется оценка тесноты связи

между явлениями (между переменными).

Тесноту связи в случае линейной зависимости характеризуют с помощью

выборочного коэффициента корреляции r_xy

r_xy - коэффициент парной корреляции (-1£ r_xy£1)

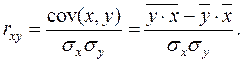
Выборочный коэффициент корреляции r_xy связан с коэффициентом линейной регрессии b соотношением

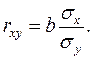
Чем ближе величина r_xy к единице, тем теснее линейная связь и тем лучше линейная зависимость согласуется с данными наблюдений. При r_xy = 1 связь становится функциональной, т. е. соотношение 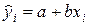выполняется для всех наблюдений.

При r_xy > 0 связь является прямой, при r_xy < 0 – обратной.

Уравнение нелинейной регрессии, также как и в линейной зависимости дополняется показателем тесноты связи между переменными 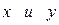, а именно индексом корреляцииR

.

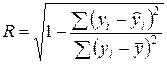Величина данного показателя находится в границах 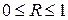; чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

В экономических исследованиях широкое применение находит такой показатель, как коэффициент эластичности, в частности, средний коэффициент эластичности.

Средний коэффициент эластичности 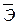показывает, на сколько процентов в среднем по совокупности значений фактора х изменится результат y от своей средней величины при изменении фактора x на 1%:

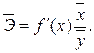
Для линейной функции: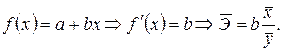

Суммарной мерой общего качества уравнения регрессии (соответствия уравнения

регрессии статистическим данным) является коэффициент детерминации R².

В случае парной регрессии коэффициент детерминации будет совпадать с квадратом коэффициента корреляции:

.

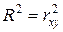В общем случае коэффициент детерминации рассчитывается по формуле:

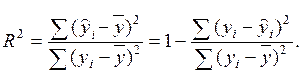(3.12)

Поясним смысл коэффициента детерминации. Пусть эмпирическое уравнение регрессии имеет вид:

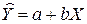
Тогда наблюдаемые (реальные) значения у_i, i = 1, 2, … , n, отличаются от модельных y_i на величину e_i:

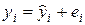
Последнее соотношение можно переписать в следующем виде:

(*)

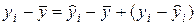где 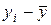− отклонение i-й (наблюдаемой) точки от среднего значения 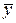зависимой переменной Y;

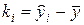− отклонение i-й точки на линии регрессии от ;

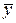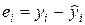− отклонение i-й точки от модельного значения 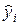, определяемого по линии регрессии.

Все отклонения рассчитываются по оси зависимой переменной (см. рис. 3.3).

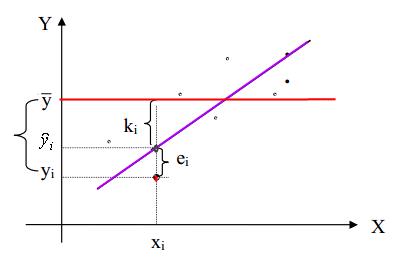
Рис.3.3.

Возведем обе части равенства (*) в квадрат и просуммируем полученные значения по объему выборки n:

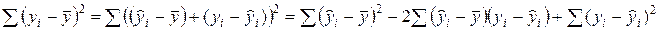
Можно показать, что 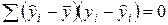(доказательство опускаем для упражнения). Тогда справедливо следующее соотношение:

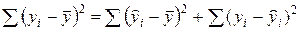(3.13)

Очевидно, что

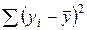− общая (полная) сумма квадратов (может интерпретироваться как мера общего разброса (рассеивания) переменной Y относительно 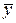). (TSS)

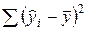− объясненная сумма квадратов, интерпретируемая как мера разброса, объяснимого с помощью регрессии. (ESS)

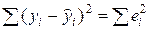− остаточная (необъясненная) сумма квадратов, являющаяся мерой остаточного, необъясненного уравнением регрессии разброса (разброса точек вокруг линии регрессии). (RSS)

Разделив (3.13) на левую его часть, получим:

.

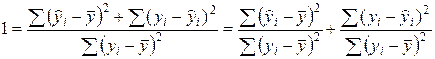Вводя обозначение 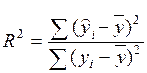, получаем соотношение (3.12). При этом очевидно, что коэффициент детерминации R² определяет долю разброса зависимой переменной, объяснимую регрессией Y на X.

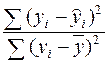определяет долю разброса зависимой переменной, необъясненную регрессией Y на X.

Из проведенных рассуждений следует, что в общем случае справедливо соотношение 0 ≤ R²≤ 1.

Коэффициент детерминации R² является мерой, позволяющей определить, в какой степени найденная прямая регрессии дает лучший результат для объяснения поведения зависимой переменной Y, чем горизонтальная прямая Y = .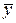

Следовательно, чем теснее линейная связь между Х и Y, тем ближе коэффициент детерминации R² к единице. Чем слабее такая связь, тем R² ближе к нулю.