Основные проблемы гидродинамического моделирования
Известно, что энергетическое состояние нефтяного или нефтегазового резервуара характеризуется полем давлений, а градиент давлений является основной движущей силой процессов фильтрации флюидов. Поэтому расчет и анализ полей давлений – обязательные атрибуты гидродинамического моделирования. Поля давлений, направления и скорости фильтрации флюидов необходимо также анализировать при выборе гидродинамических регулирующих воздействий и других методов повышения нефтеотдачи, включая гидроразрыв пласта, а также при проектировании и бурении вертикальных и наклонных, горизонтальных и многозабойных горизонтально - ветвящихся скважин.
Расчет полей давлений в резервуарах с произвольными системами гидродинамически взаимосвязанных скважин различных профилей представляет существенные трудности для большинства вычислительных методов и их программных реализаций. Эти трудности еще более возрастают при решении задач для резервуаров с тектоническими нарушениями.
При решении задач математического моделирования полей давлений в нефтяных резервуарах с системами скважин используются две технологии:
· Инженерный подход к формированию и анализу карт изобар, который может быть реализован вручную или с привлечением компьютерных технологий. В условиях реального нефтедобывающего производства карты изобар являются регламентными и формируются с периодичностью 3–6 месяцев. По ним производится оперативный анализ падения и роста давлений в отдельных зонах пласта, оцениваются скорости и направления фильтрации флюидов с возможными перемещениями контуров нефтеносности, производится расчет средневзвешенных пластовых давлений по объемам или площадям зон отбора, нагнетания и всей залежи, а также для блоков блочных систем разработки. Процедуру формирования карт изобар можно условно отнести к графо -аналитическим методам моделирования полей давлений.
Одна из основных проблем использования такого метода исследования – низкая информативность используемых исходных данных. В самом деле, для расчетов и построений карт изобар в качестве исходных данных используются, в основном, результаты обработки гидродинамических исследований специально останавливаемых скважин. Однако, сознательно недобирая остановленными скважинами нефть, за период 3 – 6месяцев удается оценить пластовые давления не более чем для 25 – 40% всего работающего фонда скважин. По этим накопившимся данным и формируется карта изобар в предположении, что все данные получены одновременно и адекватно характеризуют состояние резервуара на день её построения.
Другая группа проблем связана с применяемыми методами расчета. Формирование карт изобар обычно сводится к решению классической задачи вычислительной математики – интерполяции значений математической функции – пластовых давлений, заданных в нерегулярно расположенных точках – скважинах. Однако известные методы интерполяции сплайнами, полиномами и т.п. здесь не вполне годятся, так как получаемые результаты зачастую противоречат физическому смыслу решаемой задачи. Так, например, при использовании таких формальных методов можно получить локальные максимумы пластовых давлений между нагнетальными скважинами, а минимумы – между нефтяными скважинами, но не в них. Поэтому на практике обычно используются более простые и надежные, но менее совершенные методы, основанные на триангуляции расчетной области.
Такое графо-аналитическое моделирование затруднено для горизонтальных и горизонтально-ветвящихся скважин, для скважин с трещинами гидроразрыва пласта, для пластов с тектоническими нарушениями. Оно неадекватно отражает поле давлений в системе работающих скважин, где изменения пластовых давлений между нефтяными и нагнетательными скважинами, в соответствии с теорией фильтрации, изменяются по логарифмическому закону и существуют «воронки депрессии», «воронки регрессии». Заметим, что и проведение даже самого простого вычислительного эксперимента, например, какое будет поле давлений, если изменить режим работы одной или нескольких скважин, по этой технологии также невозможно.
· Математическое моделирование процессов фильтрации в нефтяном резервуаре с системой нефтяных, нагнетательных, пьезометрических и других скважин. Такое моделирование имеет значительно более широкие возможности и состоит в постановке и решении систем дифференциальных уравнений, описывающих процессы многофазной фильтрации флюидов в пористой среде. Решение производится одним из численных методов – обычно методом конечных разностей или конечных элементов. Такое моделирование производится в условиях научных или проектных организаций с использованием исследовательских или коммерческих версий соответствующих программных систем. Они являются системообразующим элементом так называемых постоянно действующих геолого - технологических моделей месторождений и остаются уникальными научно - техническими разработками, а их эксплуатация по-прежнему остается более искусством, нежели ремеслом.
Для математического моделирования необходим большой объем достоверных данных о геологической модели залежи, ее фильтрационных свойствах, порядке разбуривания, системе размещения, истории и режимах работы скважин, их интерференции, наличии водонасыщенных и газонасыщенных зон пласта и других факторах. Одним из основных результатов такого моделирования является расчетное поле пластовых давлений. Заметим, что расчет именно этих полей отнимает значительную часть вычислительных ресурсов компьютера: оперативную память и время работы процессора.
Основные проблемы математического моделирования полей пластовых давлений в нефтяных резервуарах с произвольными системами гидродинамически взаимосвязанных скважин:
1. Привлечение математического моделирования для решения задач оптимизации систем разработки нефтегазовых месторождений требует использования гидродинамических моделей, уровень детализации которых позволяет рассматривать скважину в качестве объекта управляющих воздействий. При этом становится возможным имитировать на моделях резервуара различные гидродинамические управляющие воздействия, связанные с изменением схем закачки и отбора жидкости скважинами: перенос фронта нагнетания, изменение направлений фильтрационных потоков, использование очаговых заводнений, перераспределение отборов по рядам скважин и участкам пласта, добуривание нагнетательных и эксплуатационных скважин, переход к более интенсивным системам разработки и др.
Вместе с тем для адекватного описания процесса эксплуатации месторождений, находящихся в разработке длительное время, необходимо иметь полноразмерные модели, способные имитировать работу большого числа гидродинамически взаимосвязанных скважин. Современные программные системы позволяют моделировать до 1500 – 2000 скважин, что становится недостаточно, так как ряд месторождений, например, Повховское, Мамонтовское, Самотлорское и другие месторождения Тюменской области имеют более 3500, 5000, 15000 скважин.
2. Интенсификация разработки нефтяной залежи может достигаться не только за счет создания более высоких градиентов давлений в системах нагнетательных и эксплуатационных скважин, но также и снижением фильтрационных сопротивлений в их призабойных зонах. Для этих целей могут использоваться бурение и эксплуатация скважин с повышенной поверхностью вскрытия продуктивного пласта: горизонтальные, наклонные, горизонтально - ветвящиеся или многозабойные. Большое разнообразие геолого - технических условий, различное состояние разработки месторождений, условия и способы эксплуатации требуют различных профилей, числа и протяженности стволов многозабойных скважин.
Для обоснованного применения горизонтальных и горизонтально–ветвящихся скважин и технологий разработки месторождений с их использованием необходимо исследование взаимодействия многозабойно - горизонтальных скважин как между собой, так и в системе с традиционными вертикальными и наклонно - ориентированными скважинами. В этих случаях расчет технологических показателей процессов разработки и моделирование фильтрационных процессов не могут быть выполнены при помощи обычных формул и моделей, применяемых для расчета взаимодействия более привычных вертикальных скважин. Поэтому создание теоретических основ проектирования разработки месторождений скважинами сложного профиля актуально и сводится, по существу, к разработке методов расчета дебитов и перепадов давлений в работе групп этих скважин.
3. Одним из наиболее эффективных методов повышения продуктивности скважин любого профиля в низкопроницаемых коллекторах является гидроразрыв пласта. При гидроразрыве в призабойных зонах нефтяных и нагнетательных скважин образуется одна или несколько вертикальных трещин, способствующих существенному снижению фильтрационных сопротивлений и увеличению притока жидкости.
Оценка эффективности и влияния гидроразрыва пласта на динамику обводнения скважин связана с анализом сложных фильтрационных процессов в окрестности скважин и вблизи высокопроводящих трещин сложных конфигураций с ускоренным продвижением флюидов по ним.
4. Для большего соответствия реальности математическое моделирование надо проводить для пластов сложных конфигураций, с нетривиальными условиями на внутренних и внешних границах пласта – контурах питания, при наличии тектонических и других нарушений в строении пластов.
5. Попытки учета вышеназванных факторов при математическом моделировании нефтегазовых резервуаров сталкиваются с общими проблемами используемых вычислительных методов.
Прежде всего, эти проблемы связаны с наличием у искомых решений соответствующих математических задач особых точек (в случае вертикальных и наклонно–ориентированных скважин), линий и кривых (для горизонтальных и горизонтально–ветвящихся скважин) или особых поверхностей (для фронтов вытеснения, различных геологических нарушений строения пласта, трещин гидроразрыва, образований макроцеликов).
Так, например, для сеточных методов расчета эти особенности побуждают сгущать расчетные сетки и требуют решения проблем пересечения особых линий и поверхностей нескольких ячеек разностной сетки под произвольными углами. Это затрудняет автоматизацию постановок и решений задач моделирования, приводит к увеличению времени счета и требуемого объема оперативной памяти компьютера, ограничивает сложность решаемых задач вплоть до принципиальной невозможности их решения данным методом.
Поэтому скважины сложного профиля, трещины гидроразрыва – объекты повышенной сложности для численного моделирования. Они требуют отказа от регулярных сеток и перехода к методам конечных элементов, граничных элементов, граничных интегральных уравнений и им подобным.
6. Математическое моделирование предполагает проведение вычислительных экспериментов. Они необходимы для многовариантных расчетов при адаптации (настройке) моделей по известной истории разработки месторождений и при решении оптимизационных задач. Поэтому методы расчета, алгоритмы и их программные реализации должны быть предельно быстрыми, а результаты математического моделирования должны быть надежными и физически содержательными. Это позволит математические модели использовать не только в исследовательских центрах, но и в условиях нефтедобывающего предприятия при формировании, например, карт изобар по ограниченному набору технологических параметров скважин – дебитов, приемистостей и давлений.
Сформулированные выше проблемы не могут быть решены инженерными методиками и трудноразрешимы в рамках привычных математических моделей, включая известные коммерческие программные системы типа ECLIPSE, MORE, VIP и др. Их решение возможно на пути разумных упрощений постановок задач, развития известных численных и численно - аналитических методов и разработки новых подходов.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Сущность моделирования процессов фильтрации флюидов в пластах.
2. Прямые задачи.
3. Обратные задачи.
4. Прямые активные задачи.
5. Прямые пассивные задачи.
6. Обратные активные задачи.
7. Обратные пассивные задачи.
8. Причины необходимости идеализации математической модели.
9. Область использования двухфазной математической модели.
10. Область использования трехфазной математической модели.
11. Область использования композиционной математической модели.
12. Сущность адаптации математической модели к известной истории разработки месторождений и работы скважин.
13. Что позволяет уточнить процесс адаптации?
14. Какие данные требуются для построения геологических моделей.
15. Какие данные требуются для построения фильтрационных моделей?
16. Для чего нужен анализ полей давления и скоростей фильтрации?
17. Инженерный подход моделирования полей давления.
18. Определение поле давления путем математического моделирования процессов фильтрации.
19. Основные проблемы математического моделирования полей пластовых давлений.
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Глава 1
Коллектора –это горные породы, которые могут служить хранилищами нефти, газа, воды и отдавать их при разработке.
Флюид – жидкость, газ, смесь жидкости и газа, то есть всякая текучая среда.
Теория фильтрации – наука, описывающая движение флюида с позиций механики сплошной среды, то есть гипотезы сплошности (неразрывности) течения.
Многофазные системы – два или больше флюида, занимают отдельные четко различимые объёмы (пузырьки газа в жидкости, капли или плёнки в газе) и взаимодействуют на поверхностях раздела.
Однофазные или гомогенные системы –многокомпонентные смеси (природный газ, нефть), в которых взаимодействие происходит на молекулярном уровне и поверхности раздела выделить нельзя.
Напряжение –нагрузка (трение соседних объёмов, внешние силы), отнесённая к единице площади.
Реологическое соотношение (закон) –- соотношение, связывающее деформацию или скорость изменения деформации с напряжением или его градиентом.
Закон Ньютона –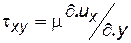 
, где ux– скорость в направлении х; у– направление, перпендикулярное х;μ – коэффициент динамической вязкости.
Фиктивный грунт – среда, состоящая из шариков одного размера, уложенных во всем объёме пористой среды одинаковым образом по элементам из восьми шаров в углах ромбоэдра.
Идеальный грунт – среда, состоящая из трубочек одного размера, уложенных одинаковым образом по элементам из четырех трубочек в углах ромба.
Недеформируемая среда–объём пустот не изменяется или изменяется так, что его изменением можно пренебречь.
Упругая ( кулоновская) среда – деформируется с линейным изменением объёма от напряжения.
Пластичная (глины), текучая(несцементируемые пески) или разрушаемаясреда–деформируется с остаточным изменением объёма, т.е. линия нагружения не совпадает с линией разгружения.
Изотропия – независимость изменения физических параметров от направления.
Анизотропия– различные изменения по отдельным направлениям.
Полная пористость – отношение объема пор к общему объему элемента.
Просветность – отношение площади просветовко всей площади сечения образца.
Открытая пористость– отношение объема открытых пор к общему объему элемента.
Динамическая (эффективная) пористость – отношение объема, занятого подвижной жидкостью, к общему объему элемента.
Эффективный диаметр частиц –диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлические сопротивление, оказываемое фильтрующейся жидкости в реальном и эквивалентном грунте, равны.
Удельная поверхность – суммарная площадь поверхности частиц, содержащихся в единице объёма.
Насыщенность – отношение объёма данного флюида, содержащегося в порах, к объёму пор.
Связанность– отношение объёма, связанного с породой флюида, к объёму пор.
Проницаемость – параметр породы, характеризующий её способность пропускать к забою скважины флюиды.
Абсолютная проницаемость – свойство породы и не зависит от свойств фильтрующегося флюида и перепада давления, если нет взаимодействия флюидов с породой, характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация.
Фазовая проницаемость – проницаемость пород для данного флюида при наличии в порах многофазных систем.
Относительная проницаемость – отношение фазовой проницаемости к абсолютной.
Трещиноватость – отношение объёма трещин ко всему объёму трещинной среды.
Густота трещин – отношение полной длинывсех трещин, находящихся в данном сечении трещинной породы к удвоенной площади сечения.
Раскрытость трещины – ширина трещины.
Скорость фильтрации – среднерасходная скорость, то есть скорость осреднённая по площади сечения породы.
Закон Дарси – линейный закон фильтрации, устанавливающий линейную связь между перепадом напора на единицу длины и объёмным расходом жидкости в грунте или горной породе.
Коэффициент фильтрации – коэффициент закона Дарси, характеризующий среду и жидкость одновременно, т.е. зависящий от размера частиц, от их формы и степени шероховатости, пористости среды, вязкости жидкости.
Критическая скорость фильтрации – скорость фильтрации, при которой нарушается закон Дарси.
Глава 2,3
Установившаяся фильтрация – параметры потока (плотность, скорость фильтрации и так далее) в каждой точке пористой среды постоянны и не зависят от времени.
Потенциальное течение – течение, при котором проекции массовой скорости на оси ортогональной системы координат будут являться производными некоторой функции по направлениям данных осей
Принцип суперпозиции – сложение фильтрационных течений.
Горное давление – давление, возникающее под действием масс горных пород средней плотности над кровлей пласта
Эффективное давление – давление между частицами пористой среды, передающаяся через поверхности контакта зёрен породы.
Одномерный поток – поток, в котором параметры являются функцией только одной пространственной координаты, направленной по линии тока.
Гидродинамически совершенная скважина – скважина, вскрывшая пласт на всю толщину и имеющая открытый забой (не имеющий дополнительного сопротивления).
Прямолинейно–параллельный поток –траектории всех частиц жидкости являются параллельными прямыми, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями, перпендикулярными траекториям.
Плоскорадиальный поток –траектории всех частиц жидкости являются прямолинейными горизонтальными прямыми, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины.
Радиально–сферический поток – траектории всех частиц жидкости являются прямолинейными горизонтальными прямыми, радиально сходящимися к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности.
Соотношение Дюпюи – уравнение притока в случае плоско-радиального течения по закону Дарси.
Индикаторная диаграмма – график зависимости дебита от депрессии.
Индикаторная зависимость –аналитическаязависимость дебита от депрессии.
Коэффициент продуктивности скважины – отношение дебита к депрессии.
Дебит – количество флюида (весовое или объёмное) в единицу времени, то есть изменение дебита на единицу депрессии.
Депрессия– разница между пластовым и забойным давлениями.
Пластовое давление – гидростатическое давление в пласте.
Забойное давление – гидростатическое давление на забое скважины.
Слоистая неоднородность (многослойный пласт) – пласт состоит из нескольких пропластков, имеющих различные фильтрационно-ёмкостные параметры..
Зональная неоднородность – пласт по площади состоит из нескольких зон с различными фильтрационно-ёмкостными параметрами.
Несовершенная скважина по степени вскрытия – скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично
Несовершенная скважина по характеру вскрытия – скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре
Параметр несовершенства – параметр характеризующий степень несовершенства скважины и равный отношению дебита несовершенной скважины к дебиту совершенной
Приведенный радиус – радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации.
Глава 4
Упруговодонапорный режим – приток жидкости поддерживается за счет напора воды, поступающей извне.
Замкнуто–упругий режим – упругий режим, в условиях ограничения залежи либо зонами выклинивания, либо экранами.
Упругий режим эксплуатации –основная форма пластовой энергии – энергия упругой деформации жидкостей и материала пласта
Жестко–водонапорный режим – вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости, а под действием внешней жидкости
Коэффициент объёмной упругости жидкости – характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу
Упругий запас – количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет объёмного расширения жидкости и уменьшения порового пространства пласта.
Коэффициент упругоёмкости пласта – показывает долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу.
Коэффициент пьезопроводности пласта – характеризует скорость распространения возмущений в пласте.
Уравнение кривой восстановления давления (КВД)– уравнение, определяющее изменение забойного давления во времени при остановке скважины.
Глава 5
Капиллярное давление (или капиллярный скачок) –разница между давлением в менее смачиваемой фазе и давлением в более смачиваемой.
Газированная жидкость – смесь жидкой и газовой фаз.
Объемный газовый фактор – отношение объемного газового дебита, приведенного к давлению в 1 ат, к объемному дебиту жидкого компонента, приведенному к тем же условиям.
Объемный коэффициент нефти – характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа, численно равен отношению удельных объемов нефти в пластовых и атмосферных условиях
Показатель «несовершенства» жидкости –характеризует степень отклонения закономерностей фильтрации от тех, какие присущи однородной несжимаемой жидкости.
Глава 6
Модель Рапопорта–Лиса – модель двухфазной фильтрации с учетом капиллярных эффектов.
Модель Баклея - Леверетта –модель двухфазной фильтрациибез учета капиллярных сил
Функция Баклея - Леверетта или функция распределения потоков фаз – отношение скорости фильтрации вытесняющей фазы к суммарной скорости, и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз.
Дисперсия волн – зависимость скорости распространения того или иного значения насыщенности от величины этой насыщенности.
Стационарные реологические жидкости – касательное напряжение зависит только от градиента скорости.
Нестационарные реологические жидкости – касательное напряжение зависит от градиента скорости и времени действия напряжений.
Вязкоупругие жидкости – среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений. Для таких сред зависимость между касательными напряжениями и градиентом скорости включает производные по времени как напряжений, так и градиента скорости.
Глава 7
Плоское движение – течение происходит в плоскостях, параллельных между собой и картина движения во всех плоскостях идентична.
Метод суперпозиции – при совместном действии в пласте нескольких стоков (эксплуатационных скважин) или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником), вычисляется по формуле для единственного стока (источника).
Метод отображения –зеркальное отображение источника (стока) относительно границы контура с присвоением дебиту знака в зависимости от вида границы.
Эксцентриситет – отклонение от центра окружности.
Нейтральные линии круговой батареи – прямые линии тока, сходящиеся в центре батареи и делящие расстояние между двумя соседними скважинами пополам.
Главные линии круговой батареи – семейство прямых линий тока, проходящее через центры скважин и делящее сектор, ограниченный двумя нейтральными линиями, пополам.
Нейтральные линии прямолинейной батареи – прямые линии тока, делящие плоскость теченияна бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями.
Главные линии прямолинейной батареи – семейство прямых линий тока, проходящее через центры скважин параллельно нейтральным линиям.
Метод эквивалентных фильтрационных сопротивлений (метод Борисова) –метод основанный на электро–магнитной аналогии и позволяющий сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки – к одиночно работающей скважине и к одиночно работающей батареи.
Внутреннее фильтрационное сопротивление – местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам за счет искривления линий тока.
Внешнее фильтрационное сопротивление – фильтрационное сопротивление потоку от контура питания к батарее скважин. Эквипотенциаль –линия равных потенциалов.
Коэффициент суммарного взаимодействия ¾ отношение суммарного дебита группы совместно действующих скважин к дебиту одиночной скважины.
Глава 8
Прямые задачи – задачи, в которых свойства пласта и жидкостей, «начальные и граничные» условия считаются известными, а определяются поля давлений, нефтенасыщенности и водонасыщенности в нефтяном пласте .
Прямые пассивные задачи – определение конфигурации подвижной границы нефтяной зоны и скорости ее продвижения с целью установления сроков прорыва вытесняющего флюида в скважины и вычисления текущего коэффициента нефтеотдачи.
Обратные задачи– определение свойств пласта и жидкостей, а также граничных и начальных условий по полям давлений, нефтенасыщенности и водонасыщенности в нефтяном пласте.
Обратные «пассивных» задачи – распознавание объектов разработки и уточнение представления о состоянии и свойствах пластовой системы.
Обратные «активные» задачи – задачи управления, регулирования процесса разработки пласта или месторождения.
Двухфазная математическая модель фильтрационного течения – моделирование процессов вытеснения нефти водой при давлениях, выше давления насыщения нефти газом.
Трехфазная математическая модель фильтрационного течения – моделирование процессов разработки нефтегазовых залежей при существенном влиянии гравитационного разделения фаз на процесс разработки.
Композиционная математическая модель фильтрационного течения – моделирование процесса разработки с учетом фазовых переходов
Адаптация математической модели к известной истории разработки месторождений и работы скважин – согласование результатов расчетов технологических показателей предшествующего периода разработки с фактической динамикой разбуривания объектов, добычи нефти, закачки воды, пластовых и забойных давлений, обводненности продукции скважин и газовых факторов.
СПИСОК ЛИТЕРАТУРЫ
1. Басниев В.С. и др. Подземная гидравлика. – М.: Недра,1986.-300с.
2. Пыхачев Г.Б., Исаев Р.Г. Подземная гидравлика. – М.: Недра,1973.– 359с.
3. Чарный И.А. Подземная гидрогазодинамика. – М.: Изд-во нефтяной и горно-топливной лит-ры, 1963. – 396с.
4. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. – М.: Недра, 1984.– 211с.
5. Евдокимова В.А., Кочина И.Н. Сборник задач по подземной гидравлике.– М.: Недра,1973.– 166 с.
6. Щелкачев В.Н., Лапук Б.Б. Подземная гидравлика. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.– 736 с.
7. Костюченко С.В., Ямпольский В.З. Мониторинг и моделирование нефтяных залежей. Томск: Изд-во НТЛ, 2000.–240с.
СОДЕРЖАНИЕ
ОБОЗНАЧЕНИЯ И РАЗМЕРНОСТИ.. 3
ВВЕДЕНИЕ. 7
1.ФИЗИЧЕСКИЕ ОСНОВЫ ПОДЗЕМНОЙ ГИДРОМЕХАНИКИ.. 7
1.1. Понятие о моделировании. 7
1.2. Модели фильтрационного течения, флюидов и коллекторов. 8
1.2.1. Модели фильтрационного течения. 8
1.2.2. Модели флюидов. 9
1.2.3. Модели коллекторов. 10
1.2.4. Характеристики коллекторов. 13
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 19
2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ФИЛЬТРАЦИИ.. 20
2.1. Скорость фильтрации. 20
2.2. Общая система уравнений подземной гидромеханики. 21
2.3. Закон Дарси (линейный закон фильтрации) 23
2.3.1. Пористая среда. 23
2.3.2. Трещинная среда. 26
2.4. Уравнения потенциального движения для пористой среды.. 27
2.5. Уравнения фильтрации для трещинно-пористой среды.. 28
2.6. Начальные и граничные условия. 29
2.6.1. Начальные условия. 29
2.6.2. Граничные условия. 30
2.7. Замыкающие соотношения. 31
2.7.1. Зависимость плотности от давления. 31
2.7.2. Зависимость вязкости от давления. 31
2.7.3. Зависимость пористости от давления. 32
2.7.4. Зависимость проницаемости от давления. 32
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 32
3. УСТАНОВИВШАЯСЯ ПОТЕНЦИАЛЬНАЯ ОДНОМЕРНАЯ ФИЛЬТРАЦИЯ 34
3.1. Виды одномерных потоков. 34
3.1.1. Прямолинейно-параллельный поток. 34
3.1.2. Плоскорадиальный поток. 35
3.1.3. Радиально-сферический поток. 36
3.2. Исследование одномерных течений. 37
3.2.1. Задача исследования. 37
3.2.2. Общее дифференциальное уравнение 37
3.2.3. Потенциальные функции. 39
3.2.4. Анализ основных видов одномерного течения. 41
3.2.5. Анализ одномерных потоков при нелинейных законах фильтрации 50
3.3. Фильтрация в неоднородных средах. 55
3.4. Приток к несовершенным скважинам. 57
3.4.1. Виды и параметры несовершенств скважин. 57
3.4.2. Исследования притока жидкости к несовершенной скважине. 59
3.5. Влияние радиуса скважины на её производительность. 62
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 63
4. НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ УПРУГОЙ ЖИДКОСТИ И ГАЗА 65
4.1. Упругая жидкость. 65
4.1.1. Понятия об упругом режиме пласта. 65
4.1.2. Основные параметры теории упругого режима. 66
4.1.3. Уравнение пьезопроводности. 67
4.1.4. Приток к скважине в пласте неограниченных размеров. 68
4.1.5. Приток к скважине в пласте конечных размеров в условиях упруговодонапорного и замкнутоупругого режимов. 72
4.1.6. Периодически работающая скважина. 75
4.1.7. Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами. 76
4.2. Неустановившаяся фильтрация газа в пористой среде. 78
4.2.1. Уравнение Лейбензона. 78
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 79
5.ОСНОВЫ ТЕОРИИ ФИЛЬТРАЦИИ МНОГОФАЗНЫХ СИСТЕМ.. 81
5.1. Связь с проблемой нефтегазоотдачи пластов. 81
5.2. Основные характеристики многофазной фильтрации. 81
5.3. Исходные уравнения многофазной фильтрации. 86
5.4. Потенциальное движение газированной жидкости. 87
5.5. Фильтрация водонефтяной смеси и многофазной жидкости. 93
5.6. Одномерные модели вытеснения несмешивающихся жидкостей. 95
5.6.1. Задача Баклея - Леверетта и ее обобщения. 97
5.6.2. Задача Рапопорта – Лиса. 99
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 100
6.ОСНОВЫ ФИЛЬТРАЦИИ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ.. 102
6.1. Реологические модели фильтрующихся жидкостей и нелинейныезаконы фильтрации 102
6.2. Одномерные задачи фильтрации вязкопластичной жидкости. 105
6.3. Образование застойных зон при вытеснении нефти водой. 108
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 109
7. УСТАНОВИВШАЯСЯ ПОТЕНЦИАЛЬНАЯ ПЛОСКАЯ (ДВУХМЕРНАЯ) ФИЛЬТРАЦИЯ.. 110
7.1. Метод суперпозиции (потенциалов) 111
7.1.1. Фильтрационный поток от нагнетательной скважины к эксплуатационной 113
7.1.2. Приток к группе скважин с удаленным контуром питания. 115
7.1.3. Приток к скважине в пласте с прямолинейным контуром питания 116
7.1.4. Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы.. 117
7.1.5. Приток к скважине в пласте с произвольным контуром питания 118
7.1.6. Приток к бесконечным цепочкам и кольцевым батареям скважин 119
7.2. Метод эквивалентных фильтрационных сопротивлений. 125
7.3. Интерференция несовершенных скважин. 130
7.3.1. Взаимодействие скважин в анизотропном пласте. 130
7.3.2. Взаимодействие скважин при нестационарных процессах. 132
7.4. Решение плоских задач фильтрации методами теории функций комплексного переменного. 134
7.4.1.Общие положения теории функций комплексного переменного. 134
7.4.2. Характеристическая функция, потенциал и функция тока. 135
7.4.3. Характеристические функции некоторых основных типов плоского потока 138
7.4.4. Характеристическая функция течения при совместном действии источника и стока. 142
7.4.5. Характеристическая функция течения для кольцевой батареи скважин 144
7.4.6. Подсчет времени движения частицы несжимаемой жидкости вдоль линии тока. 146
7.4.7. Стягивание контура нефтеносности к эксплуатационной кольцевой батарее 147
7.5. Метод конформного отображения. 151
7.5.1. Общие положения. 151
7.5.2. Вывод некоторых формул для притока к скважинам при помощи конформного отображения. 152
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 157
8. ОСНОВЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ 159
8.1. Сущность математического моделирования. 160
8.2. Основные проблемы гидродинамического моделирования. 163
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.. 168
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ.. 170
СПИСОК ЛИТЕРАТУРЫ..... 178