Основные свойства математического ожидания и дисперсии

Свойство 1. Математическое ожидание постоянной равно этой постоянной:

.

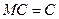Доказательство. Постоянную C можно рассматривать как дискретную случайную величину, принимающую единственное значение с вероятностью единица, поэтому MС = 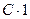= 1.

Свойство 2. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:

M(X + Y) = MX + MY.

Следствие. Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий.

Свойство 3. Математическое ожидание произведения независимых случайных величин X и Y равно произведению математических ожиданий этих величин. Пусть случайные величины X и Y заданы рядами распределения. Ряд распределения для произведения случайных величин выглядит следующим образом:

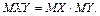
Причем в силу независимости случайных величин X и Y события независимы.

Следствие. Постоянный множитель можно выносить за знак математического ожидания:

M(cX) = cMX.

Доказательство. Постоянную c можно рассматривать как случайную величину, причем c и X – независимые случайные величины, поэтому

M(cX) = McMX = СМХ.

Свойство 4. Дисперсия постоянной величины равна нулю:

D(C) = 0.

Доказательство. Согласно свойству 1,

.

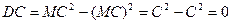Свойство 5. Постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат, т. е.

D(c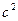X) = D(X).

Свойство 6. Дисперсия суммы (разности) независимых случайных величин X и Y равна сумме их дисперсии:

D(X + Y) = D(X) + D(Y),

D(X – Y) = D(X) + D(Y).

Задача. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

Х	– 5
Р	– 0,4	0,3	0,1	0,2

Решение: Можно вычислить дисперсию, исходя из определения дисперсии, однако мы воспользуемся формулой D(X) = M(X²) – (M(X))². Найдем математическое ожидание Х:

М(Х) = –5×0,4 + 2×0,3 + 3×0,1 + 4×0,2 = –0,3.

Напишем закон распределения Х²:

Х2	– 25
Р	– 0,4	0,3	0,1	0,2

Найдем математическое ожидание Х²:

М(Х²) = 25×0,4 + 4×0,3 + 9×0,1 + 16×0,2 = 15,3.

Найдем искомую дисперсию:

D(X) = M(X²) – (M(X))² = 15,3 – (–0,3)² = 15,21.

Моменты случайной величины

1. 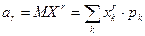– начальный момент,

2. 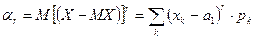– центральный момент,

3. 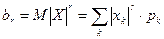– абсолютный,

4. 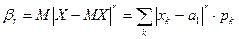– абсолютный центральный.

Первые моменты играют важную роль в статистике при нахождении параметров функции распределения.

Если кривая распределения f(x) непрерывной случайной величины X симметрично расположена относительно оси, проходящей через M(X), то все центральные моменты нечетного порядка равны нулю. То же самое заключение можно сделать по поводу дискретной случайной величины X, если ее полигон симметричен относительно оси, проходящей через среднее значение случайной величины.