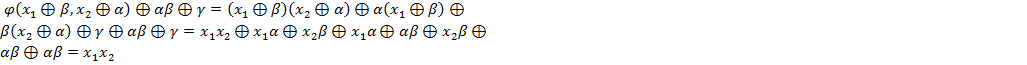Замыкание. Основные замкнутые классы
Полином Жегалкина
Конъюнкция вида 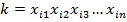 называется монотонной конъюнкцией (отсутствует отрицание переменных).
называется монотонной конъюнкцией (отсутствует отрицание переменных).
Полиномом Жегалкина от n переменных называется сумма по модулю 2 различных монотонных конъюнкций, составленных из этих переменных.
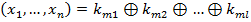 ,
, 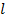 – длина полинома.
– длина полинома.
Жегалкин рассматривал только операции конъюнкции и сложения по модулю 2.
В алгебре с этими операциями справедливо:
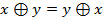
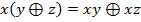
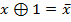
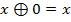
Теорема: для любой булевой функции существует полином Жегалкина, представляющий данную функцию и причём только один.
Доказательство: существование следует из того, что для любой булевой функции можно построить СДНФ, далее дизъюнкцию и отрицание можно заменить на конъюнкцию и сложение по модулю 2.
Докажем единственность. Рассмотрим множество булевых функций от 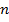 переменных -
переменных - 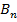 . Число булевых функций равно
. Число булевых функций равно 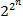 . Покажем, что число полиномов Жегалкина от
. Покажем, что число полиномов Жегалкина от 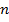 переменных тоже
переменных тоже 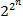 и тогда, так как для любой функции существует полином Жегалкина, для каждой функции такой полином будет единственный.
и тогда, так как для любой функции существует полином Жегалкина, для каждой функции такой полином будет единственный.
Общий вид полинома Жегалкина от трёх переменных:
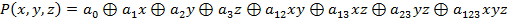
 перестановок
перестановок
Полином Жегалкина от 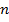 переменных мы представим как
переменных мы представим как
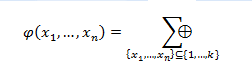
т.к. число слагаемых равно числу подмножество множества из 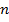 элементов, то оно будет равно
элементов, то оно будет равно 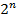 . Каждый
. Каждый 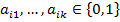 поэтому число полиномов Жегалкина совпадает с числом
поэтому число полиномов Жегалкина совпадает с числом 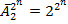 .
.
Замыкание. Основные замкнутые классы.
Рассмотрим множество 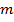 булевых функций
булевых функций 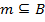
Замыканием класса 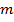 называется множество функций, представляющих собой суперпозиции различных функций класса
называется множество функций, представляющих собой суперпозиции различных функций класса 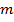
(само 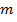 входит). Обозначение:
входит). Обозначение: 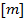
Свойства:
1. 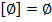
2. 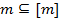
3. 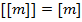
4. 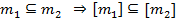
5. 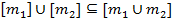
Класс функций 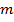 называется замкнутым, если он совпадает со своим замыканием.
называется замкнутым, если он совпадает со своим замыканием. 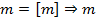 - замкнутый.
- замкнутый.
Основные замкнутые классы:
1. Класс 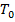 (булевы функции, сохраняющие константу 0)
(булевы функции, сохраняющие константу 0)
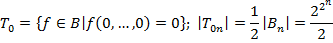
Лемма: класс 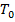 замкнут.
замкнут.
Доказательство: возьмём 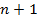 функцию:
функцию: 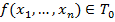 и
и 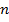 функций от
функций от 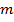 переменных вида
переменных вида 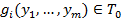
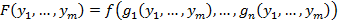
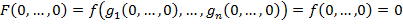
2. Класс 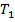 (булевы функции, сохраняющие константу 1)
(булевы функции, сохраняющие константу 1)
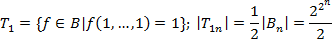
Лемма: класс 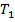 замкнут.
замкнут.
Доказательство: возьмём 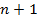 функцию:
функцию: 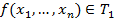 и
и 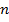 функций от
функций от 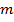 переменных вида
переменных вида 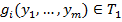
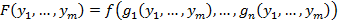
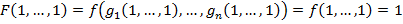
3. Класс S (самодвойственные функции).
Функция называется самодвойственной, если она совпадает со своей двойственной (на противоположенном наборе принимает противоположенное значение).
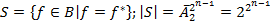
Лемма: класс 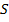 замкнут.
замкнут.
Доказательство: возьмём 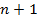 функцию:
функцию: 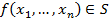 и
и 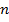 функций от
функций от 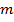 переменных вида
переменных вида 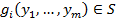
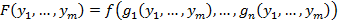
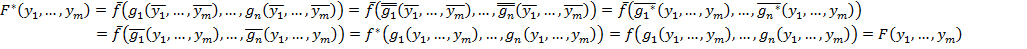
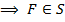
Лемма: (о несамодвойственной функции)
Пусть 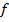 – несамодвойственная функция
– несамодвойственная функция 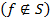 , тогда из неё путём подстановки вместо её переменных
, тогда из неё путём подстановки вместо её переменных  выражение
выражение 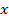 или
или 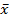 можно получить несамодвойственную функцию одной переменной, т.е. константу.
можно получить несамодвойственную функцию одной переменной, т.е. константу.
Доказательство: 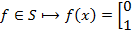
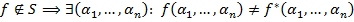
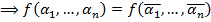
С использованием набора  формируем функцию
формируем функцию
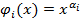 , это функция от одной переменной
, это функция от одной переменной 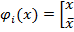
Формируем функцию 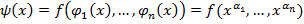
Покажем, что данная функция является константой.
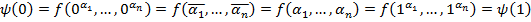
4. Класс 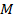 (монотонные функции)
(монотонные функции)
Рассмотрим 2 набора 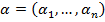 и
и 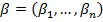 из
из 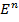 ; будем говорить, что
; будем говорить, что 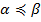 (
( 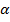 предшествует
предшествует 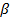 ), если
), если 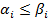
Таким образом на множестве 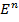 мы ввели бинарное отношение предшествования, которое является отношением частичного порядка.
мы ввели бинарное отношение предшествования, которое является отношением частичного порядка.
Булева функция 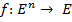 называется монотонной, если
называется монотонной, если
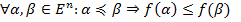
Лемма: класс 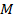 является замкнутым.
является замкнутым.
Доказательство: возьмём 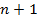 функцию:
функцию: 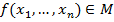 и
и 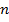 функций от
функций от 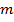 переменных вида
переменных вида 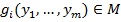
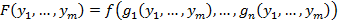
Рассмотрим 2 набора 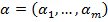 и
и 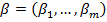 , такие, что
, такие, что 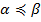 ; так как
; так как 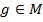
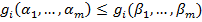
Обозначим значения 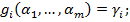
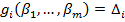 , то есть
, то есть 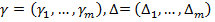 и
и 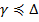 по предположению.
по предположению.
В силу монотонности 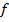
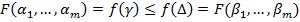
Таким образом, из того, что 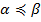 мы получили
мы получили 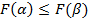 , значит
, значит  - монотонна.
- монотонна.
Лемма: (о немонотонной функции)
Если функция 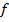 не является монотонной, то из неё путём подстановки вместо её переменных
не является монотонной, то из неё путём подстановки вместо её переменных  констант 0,1 и функции
констант 0,1 и функции 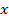 можно получить немонотонную функцию одной переменной, т.е. константу.
можно получить немонотонную функцию одной переменной, т.е. константу.
Доказательство: рассмотрим функцию 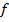 , тогда
, тогда 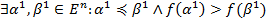 . Покажем, что в этом случае существуют 2 соседних набора
. Покажем, что в этом случае существуют 2 соседних набора 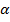 и
и 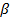 :
: 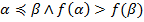
1) Если 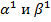 уже соседние, то
уже соседние, то 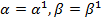
2) Пусть 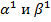 не соседние и пусть они отличаются на t координат (у
не соседние и пусть они отличаются на t координат (у 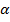 - это 0, а у
- это 0, а у 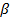 - это 1). Строим цепочку соседних наборов. Переходим с помощью соседних наборов.
- это 1). Строим цепочку соседних наборов. Переходим с помощью соседних наборов. 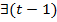 набор
набор 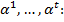
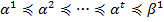 и каждая пара связана соседством. При чём, так как
и каждая пара связана соседством. При чём, так как 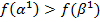 , то по хотя бы на одной паре двух соседних наборов, которые обозначаются как
, то по хотя бы на одной паре двух соседних наборов, которые обозначаются как 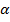 и
и 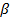 выполняется такое же неравенство
выполняется такое же неравенство 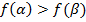 . Предположим, что полученные нами
. Предположим, что полученные нами 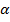 и
и 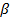 отличаются по s-той координате, т.е.
отличаются по s-той координате, т.е. 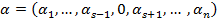 и
и 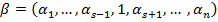 . Рассмотрим функцию
. Рассмотрим функцию 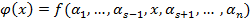 , тогда,
, тогда, 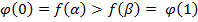 . Мы получили, что
. Мы получили, что 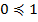 , но
, но 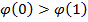 , таким образом
, таким образом 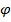 - немонотонная функция одной переменной
- немонотонная функция одной переменной 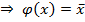
5. Класс 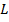 (линейные функции)
(линейные функции)
Функция 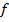 называется линейной, если её полином Жегалкина имеет степень не больше 1.
называется линейной, если её полином Жегалкина имеет степень не больше 1.
Лемма: пусть 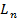 - множество линейных функций от
- множество линейных функций от 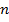 переменных, тогда мощность этого множества
переменных, тогда мощность этого множества 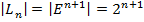
Доказательство: множество функций однозначно определяется набором своих коэффициентов 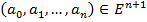
Лемма: класс 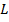 замкнут
замкнут
Доказательство:
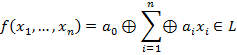
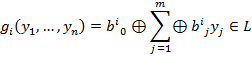
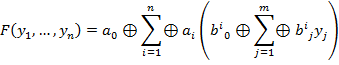
При раскрытии знаков суммирования, переменные сохраняют первую степень.
Лемма: (о нелинейной функции)
Пусть 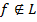 тогда из этой функции путем подстановки вместо её переменных
тогда из этой функции путем подстановки вместо её переменных  констант 0,1 и функций
констант 0,1 и функций 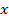 или
или 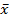 , а так же, если необходимо, взятия отрицания над всей функцией, можно получить нелинейную функцию
, а так же, если необходимо, взятия отрицания над всей функцией, можно получить нелинейную функцию 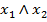 .
.
Доказательство: 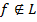 тогда её полином Жегалкина включает слагаемые, имеющие 2 и более сомножителей. Пусть среди таких слагаемых есть слагаемые, включающие
тогда её полином Жегалкина включает слагаемые, имеющие 2 и более сомножителей. Пусть среди таких слагаемых есть слагаемые, включающие 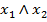 , тогда представим функцию
, тогда представим функцию 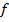 в виде:
в виде:
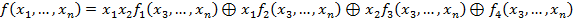
В силу того, что полином Жегалкина для 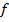 – единственный
– единственный
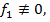 тогда
тогда 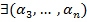 :
: 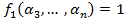 . Берем этот набор и вычитаем от него значение других функций:
. Берем этот набор и вычитаем от него значение других функций: 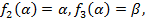
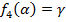 .
.
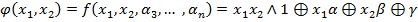
На базе 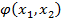 построим
построим 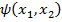 =
=