Тематика письменных работ по курсу. 1. Нормальный закон распределения

Тематика рефератов:

1. Нормальный закон распределения.

2. Теорема Чебышева и ее практическое значение.

Тематика контрольных работ:

1. Элементы комбинаторики. Непосредственное вычисление вероятностей.

2. Основные теоремы теории вероятностей.Повторные независимые испытания.

Дискретные случайные величины.

3. Числовые характеристики вариационных рядов.

4 .Статистические оценки параметров распределения.Методы нахождения оценок.

Тестовые задания для самоконтроля:

1. В урне содержится 4 белых , 5 красных и 6 черных шаров. Наудачу вынимают один шар. Какова вероятность того, что он красный?

A) 1/3

B) 1/5

C) 1/4

D) 2/3

E) 1

2. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна семи.

A) 1/3

B) 2/3

C)1/2

D)1/6

E) 1/10

3. Сколько различных шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если цифры не повторяются?

A) 720

B) 360

C) 120

D) 180

E) 240

4. Сколькими способами можно выбрать три сотрудника на три одинаковые должности из десяти претендентов?

A) 720

B) 360

C) 120

D) 180

E) 240

5. Сколькими способами можно выбрать три сотрудника на три различные должности из десяти претендентов?

A) 720

B) 360

C) 120

D) 180

E) 240

6. В урне содержится 3 белых и 7 черных шаров. Из урны вынули два шара (не возвращая вынутый шар в урну). Какова вероятность того, что оба шара окажутся черными?

A) 6/15

B) 8/15

C) 7/10

D) 9/15

E) 7/15

7. Два стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,7, для второго - 0,8. Какова вероятность того, что цель будет поражена?

A) 0,38

B) 0,56

C) 0,06

D) 0,94

E) 0,96

8. Всхожесть семян пшеницы составляет 80 %. Найти вероятность того, что из 5 посеянных семян взойдут ровно 3.

A) 0,496

B) 0,008

C) 0,7952

D) 0,512

E) 0,2048

9. Математическое ожидание М(X) случайной величины Х, заданной законом распределения

Х		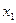	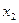…	xn
P		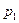	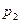…	pn

определяется равенством:

A)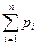

B)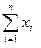

C)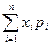

D)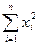

E)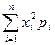

10. Дисперсией случайной величины Х называют:

A) M[X – M(X)]²

B) M(X ²)

C) M ²(X)

D) M(Х ²) – M(X)

E) M[X – M(X ²)]

11. Найти математическое ожидание М(X) случайной величины Х, зная закон её распределения:

Х
P	0,2	0,3	0,5

A) 3,4

B) 2,6

С) 2,8

D) 2,4

E) 0,76

12. Найти дисперсию D(X) случайной величины Х, зная закон её распределения:

Х
P	0,3	0,2	0,5

A) 3,4

B) 2,6

С) 2,8

D) 2,4

E) 0,76

13. Случайная величина X задана функцией распределения:

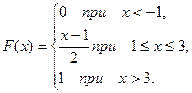
Вычислить вероятность попадания случайной величины X в интервал (1,5; 2,5).

A) 2

B) 1

C)1/2

D)1/6

E) 1/3

14. Случайная величина Х задана функцией распределения:

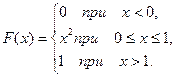
Найти плотность вероятности 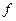(х) на интервале (0,1).

A)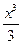

B) х²

C) 0

D) 2х

E) 1

15. Случайная величина Х задана функцией распределения:

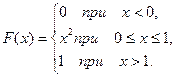
Найти математическое ожидание М(X).

A) 2/3

B) 1

C) 1/3

D)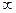

E) 0

16. Случайная величина Х задана функцией распределения:

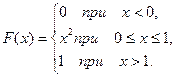
Найти дисперсию D(X).

A) 2/3

B) 1/2

C) 0

D) 1/4

E) 1/18

17. Математическое ожидание и дисперсия случайной величины X, распределённой по биномиальному закону, находятся по формулам:

A) M(X) = a, D(X) = 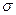²

B) M(X) = np, D(X) = npq

C) M(X) = p, D(X) = q

D) M(X) = npq, D(X) = np

E) M(X) = 1, D(X) = 0

18. Выборка задана следующей таблицей:

xi
ni

Найти выборочную среднюю .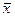

A) 5

B) 6

C) 5,76

D) 4,65

E) 3

19. Из генеральной совокупности извлечена выборка:

xi
ni

Найти несмещенную оценку генеральной средней (выборочную среднюю ).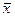

A) 18

B) 4

C) 3

D) 6

E) 30

20. Выборка задана следующей таблицей:

xi	0,5	–2
ni

Найти несмещенную оценку дисперсии (исправленную дисперсию).

A) 5

B) 6

C) 10,95

D) 4,65

E) 1

21. Дан дискретный вариационный ряд выборки:

xi
ni

Найти моду вариационного ряда:

A) 20

B) 10

C) 16

D) 3

E) 4

22. Дан дискретный вариационный ряд выборки:

xi
ni

Найти медиану вариационного ряда.

A) 1

B) 3

C) 20

D) 2

E) 2,5

23. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 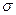= 9. Найти доверительный интервал для оценки неизвестного математического ожидания а по выборочной средней 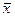=18,31, если объем выборки п = 49 и задана надежность оценки 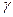= 0,95. (По таблице найдено

t = 1,96).

A) (15,79; 20,83)

B) (17,138; 19,882)

C) (16,23; 18,65)

D) (14,83; 17,12)

E) (15,8; 21,02

24. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 9 найдены выборочная средняя 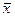=30,1 и «исправленное» среднее квадратическое отклонение 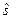= 6. Оценить математическое ожидание при помощи доверительного интервала с надежностью 0,99. (По таблице найдено 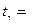3,36).

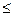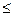A) 24,23 a 39,37

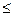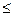B) 22,04 a 35,96

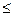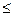C) 23,38 a 36,82

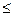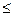D) 23,63 a 42,77

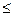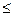E) 25,25 a 36,7

25. Случайная величина Х распределена по нормальному закону. Найти методом максимального правдоподо­бия точечную оценку неизвестного параметра а нормального распределения по выборке:

xi
ni

A) 3,3

B) 4

C) 0,5

D) 0,59

E) 0,9