Изучение механических моделей тканей
Пассивные механические свойства биологических тканей (не связанные с процессами сокращения мышц) характеризуются двумя величинами:
- ...................................,………………………………………….
- .....................................................................................................

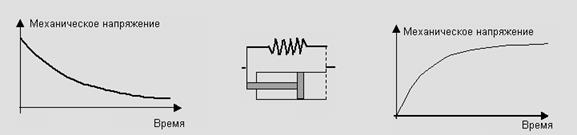
Поясните рисунки………………………………………………………
…………………………………………………………………………...
…………………………………………………………………………...
…………………………………………………………………………
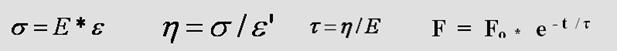
Поясните формулы……………………………………………………..
…………………………………………………………………………...
…………………………………………………………………………...
…………………………………………………………………………...
…………………………………………………………………………...
Запишите и сформулируйте закон Гука……………………………
…………………………………………………………………………
…………………………………………………………………………
Запишите и сформулируйте закон пластической деформации.......
………………………………………………………………………..
………………………………………………………………………..
……..…………………………………………………………………
Практическая часть.
1.Для упругого элемента, считая пружину в виде упругого жгута с соответствующими размерами, которые необходимо измерить, определите значение модуля юнга…………………………………
………………………………………………………………………..
………………………………………………………………………..
………………………………………………………………………….
2.Для пластичного элемента, считая пружину в виде упругого жгута с соответствующими размерами, которые необходимо измерить, определите значение модуля юнга………………….
………………………………………………………………………..
………………………………………………………………………….
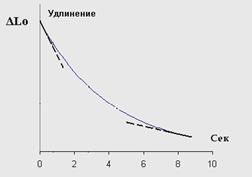
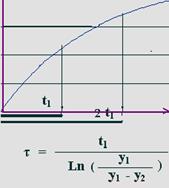
3. Для модели Максвелла измерьте время, за которое удлинение упругого элемента (как и механическое напряжение) уменьшается от значения Х1. до значения Х2. и далее до значения X3. Опыт проведите три раза и возьмите средние значения по проведенным измерениям. Например, получились такие данные: В момент времени t = 0, сила упругости динамометра была равна F0 = 3,2 Н. В момент t1 = 2,1 c мы получили показание динамометра 3,1 Н. Тогда в соответствии с последним уравнением
3,1 = 3,2 * eхр ( - t1/ τ ), выражаем тау:
τ = 2,1 / (Ln(3,2) - Ln(3,1).
 | …………………………………………. …………………………………………. …………………………………………. …………………………………………. …………………………………………. …………………………………………. …………………………………………. |
Полупроводниковый терморезистор
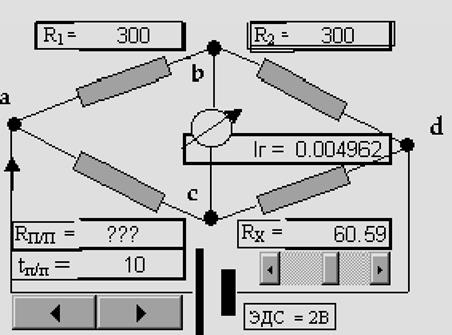
Вывод формулы компенсационного метода:
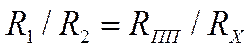
Выберем точку наименьшего потенциала для приведенной схемы на рисунке за точку нулевого потенциала: это точка d. Тогда потенциал точки в (φв) равен напряжению на резисторе R2.
φв = U2. Потенциал точки с (φс) равен напряжению на резисторе Rх. φс = Uх. Разность потенциалов между точками в и с выражается, поэтому как разность напряжение (U2- Uх):
φв – φс = (U2- Uх).
Выразим эти напряжения по закону Ома:
U2 = Iabd * R2,
UX = Iacd * RX.
Здесь токи Iabd , Iacd, это токи, которые протекают в верхней и нижней ветви схемы. Эти токи можно выразить по закону Ома для замкнутых контуров, включающих источник ЭДС с внутренним сопротивлением, которым можно пренебречь.
Iabd =Е / (R1+R2),
Iacd = Е / (RПП+RХ).
Подставим эти формулы в формулу для разности потенциалов между точками в и с:
φв – φс = (U2- Uх) = (Iabd * R2) – (Iacd * RX) = (Е* R2) / (R1+R2) – (Е * RX)/ (RПП+RХ) =
{Е * R2* (RПП+RХ) - Е * RX * (R1+R2)} / {(R1+R2) * (RПП+RХ)}. Теперь чтобы убедиться, когда эта разность потенциалов будет равна нулю, достаточно приравнять нулю числитель правой части этого уравнения: {Е * R2* (RПП+RХ) - Е * RX * (R1+R2)} = 0. После соответствующих преобразований получается формула: 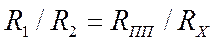
Практическая часть.
Вам требуется получить в опыте график зависимости , приведенный на рисунке. И по измеренному значению сопротивления найти неизвестную температуру обрахца…
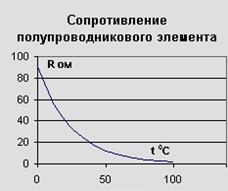
………………………………………………………………………..
………………………………………………………………………….
………………………………………………………………………..
………………………………………………………………………….
………………………………………………………………………..
………………………………………………………………………….
………………………………………………………………………..
………………………………………………………………………….
………………………………………………………………………..
………………………………………………………………………….
………………………………………………………………………..
…………………………………………(Вклеить полученный график)
