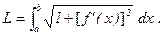Асимптоты графиков функций.

а) Вертикальные асимптоты. Прямая х=х₀ называется вертикальной асимптотой кривой y=f(x), если хотя бы один из пределов 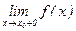, , 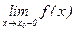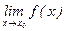равен бесконечности.

Примеры.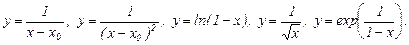

ПРАВИЛО. Для определения вертикальных асимптот графика следует найти особые точки функции и затем найти пределs в этих особых точках.

Пример.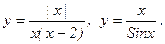

б) Горизонтальная асимптота. Прямая y=h называется правой горизонтальной асимптотой кривой y=f(x) , если 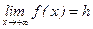. Аналогично определяется левая горизонтальнаяасимптота.

Примеры. .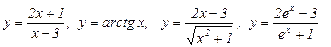

б) Наклонная асимптота.

Определение. Прямая у=кх+b называется правой (при х®+¥) асимптотой кривой y=f(x), если

f(x)=kx+b+a(x) при х®+¥.

Аналогично дается определение левой асимптоты (при х® – ¥).

Примеры.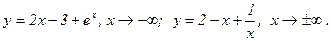

Примечание. Для рациональных функций правая и левая асимптоты совпадают.

Примечание. Горизонтальная асимптота представляет собой ЧАСТНЫЙ СЛУЧАЙ наклонной асимптоты.

Методы нахождения наклонных асимптот.

1) Деление уголком для рациональных функций. Случаи а) [cт. числителя] – [ст. знаменателя] ³ 2, нет асимптоты, б) [ст. числ.] – [ст. знам.] = 1, есть наклонная асимптота, в) [ст. числ.] = [ст. знам.] есть горизонтальная асимптота, параллельная оси Х, г) [ст. числ.] < [ст. знам.], асимптотой является ось Х. Правые и левые асимптоты для рациональных функций совпадают.

2) Общий метод. Используя определение f(x)=kx+b+a(x), х® ¥ , вывести формулы для коэффициентов k , b. ,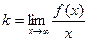

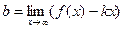
Примеры.

Приме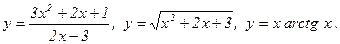чание. Если хотя бы один из пределов не существует, то асимптоты нет:

.

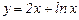3) Использование стандартных разложений Маклорена для нахождения асимптот (при наличии времени).

Примеры.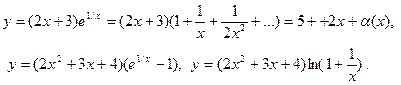

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Обратные операции.

рассмотрим равенство SinA = B. Перекинем операцию Sin в правую часть равенства и заменим её на обратную. Получим A=arcsinB. Аналогичные действия можно проделать с операцией взятия дифференциала. В этом случае обратная операция - это интеграл

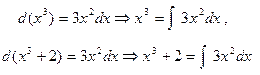
При таком определении не нужно объяснять, зачем под знаком интеграла нужно писать этот дурацкий и никому не нужный dx

Примечание. Нет однозначности для обратной операции.

Определение. Функция F(x) называется первообразной функции f(x) на отрезке (a, b), если F’(x)ºf(x) для всех xÎ(a, b). Примеры. Путь (перемещение) S(t) – первообразная для скорости V(t)

ЛЕММА (необходимое и достаточное условие постоянства функции на интервале). Для того чтобы функция Ф(х) была постоянна на интервале (а,b) необходимо и достаточно, чтобы её производная была равна нулю на этом интервале.

Д-во: 1) Ф(х)=С Þ Ф’(x)=0 . 2) Ф’(x)º0 Þ Ф(х₂)–Ф(х₁)=Ф’(c)(x₂–x₁)=0 или Ф(х₂) = Ф(х₁).

Следствие. Разность двух первообразных данной функции постоянна. Д-во.

Вывод. Множество всех первообразных данной функции имеет вид F(x) + C.

Определение. Множество всех первообразных данной функции называется неопределенным интегралом; запись 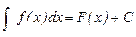. Терминология: подынтегральная функция f(x), подынтегральное выражение f(x)dx.

Задача: Найти f(x), если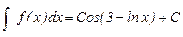

Свойства неопределенного интеграла.

а) Производная от неопределенного интеграла равна подынтегральной функции.

б) Дифференциал от неопределенного интеграла равен подынтегральному выражению. Д-ВО.

в) Линейность

ТАБЛИЧНЫЕ ИНТЕГРАЛЫ (14 штук)

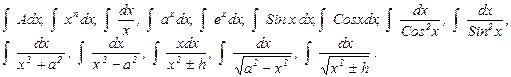
Доказательство любого интегрального равенства – дифференцирование с использованием свойства а).

Теорема о линейной подстановке.

Если 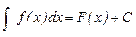, то 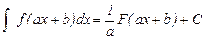. Д-во.

Примечание. Множитель 1/а называется поправкой интегрирования.

Примеры.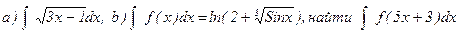

Замена переменной.

Равенство 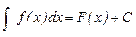останется справедливым, если независимую переменную заменить произвольной дифференцируемой функцией, т.е.

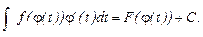Д-во

Пример. 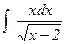. Замена x = t² + 2.

Рекомендации. Если в подынтегральном выражении имеется 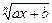, то его обозначают через t .

Если в подынтегральном выражении имеется квадратный трехчлен, то можно попробовать сделать замену х = t – b/2a.

Пример (форма записи).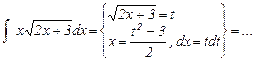

Подведение под знак дифференциала.

Равенство d(Sinx) = Cosx dx можно читать справа налево: Cosx dx = d(Sinx). В этом случае можно говорить о подведении функции Cosx под знак дифференциала. Популярные подведения под d( )

xdx, (1/x)dx, e^xdx, Sinx dx, Cosx dx .

Пример. 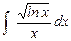. Подведение под знак дифференциала – это форма замены переменной!!!

Теорема о линейной подстановке – частный случай подведения под знак дифференциала!!!

Интегрирование по частям.

Вывод формулы: .

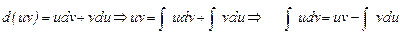Пример (форма записи):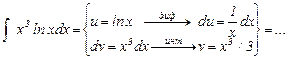

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ

а) Интегрирование многочленов сводится к табличным интегралам.

б) Неправильная рациональная дробь = многочлену + правильная дробь.

в) Вывод: нужно научиться интегрировать правильную дробь.

г) Разложение многочлена на множители. Случай простых действительных корней знаменателя.

Теорема. Правильная рациональная дробь с простыми корнями в знаменателе равна сумме своих асимптотик в особых точках.

Асимптотики находятся методом «затыкания» (в знаменателе закрываем линейный множитель и подставляем во всю дробь то, что раньше нельзя было подставить.

Иллюстрация на примере

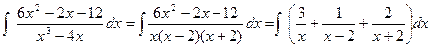
Простейшие дроби I типа и их интегрирование.

д) Разложение многочлена на множители. Случай кратных действительных корней знаменателя.

Простейшие дроби II типа и их интегрирование.

Метод разложения правильной дроби на простейшие.

е) Разложение многочлена на множители. Случай комплексно-сопряженных корней знаменателя.

Простейшие дроби III типа и их интегрирование.

Метод разложения правильной дроби на простейшие.

KANT LIVANOV , 2011

Для особо одаренных лохов..

Производные

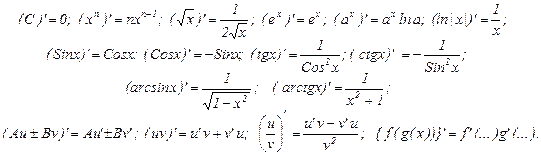
Для «особо одарённых»: – это не дробь!!! Это .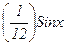

Интегралы

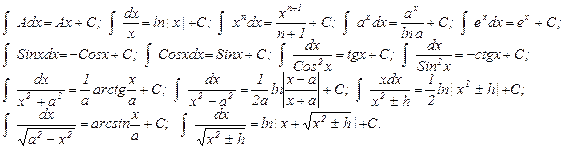
Память о школьной Мариванне:

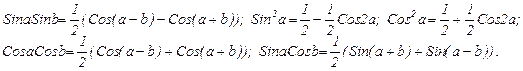
Линейная подстановка 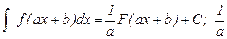– поправка интегрирования.

Популярные замены переменных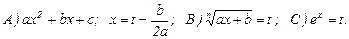

Популярные подведения под знак дифференциала

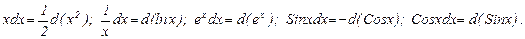
Интегрирование по частям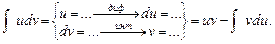

Интегрирование ПРАВИЛЬНОЙ рациональной дроби с ПРОСТЫМИ корнями в знаменателе

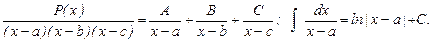
Коэффициенты А, В, С находятся методом «затыкания».

Для разложения знаменателя на множители вспомним родную Мариванну

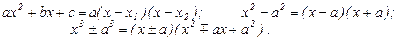
Приложения определенного интеграла необходимые для ДР

Теорема об оценке 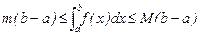. Площадь фигуры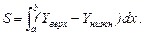

Объем тела с переменным сечением .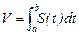

Объём тела вращения 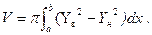Длина дуги