Практика 2. Действия над матрицами, сложение, умножение.

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Математика

(1 семестр, часть 1)

Учебно-методическое пособие

для специальностей:

09.03.03 «прикладная информатика в экономике»

(группы 446-1 и 446-2)

Томск

ТУСУР

Электронное учебное пособие составлено и скорректировано с учётом реального проведения практических занятий на ФСУ в группах 446-1, 446-2 осенью 2016 года. В осеннем семестре, согласно рабочим программам, на специальности 09.03.03 изучаются следующие темы: линейная алгебра, аналитическая геометрия, введение в математический анализ, дифференциальное исчсиление. Даны с подробным разбором задачи, которые решались на каждом практическим занятии. Задачи для домашнего задания даны в контексте рассмотрения темы, по ходу урока, то есть видно, после разбора каких задач будет сразу легко понять, как решить это домашнее задание. Может представлять методический интерес для преподавателей, работающих на аналогичных специальностях, как материал для планирования занятий.

Номера практик по датам для групп 446-1, 446-2 согласно расписанию

Практика №	446-1	446-2
	02.09.16	03.09.16
	06.09.16	03.09.16
	09.09.16	09.09.16
	16.09.16	17.09.16
	20.09.16	17.09.16
	23.09.16	23.09.16
	30.09.16	27.09.16
	04.10.16	27.09.16
	07.10.16	07.10.16
	14.10.16	11.10.16
	18.10.16	11.10.16
	21.10.16	21.10.16
	25.10.16	25.10.16
	28.10.16	25.10.16

Практика 1.Входной тест по школьной программе.

(неравенства с модулем, логарифмические неравенства, задачи на движение).

Практика 2. Действия над матрицами, сложение, умножение.

Задача 1.Найти произведение матриц , .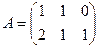

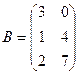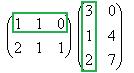
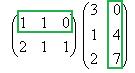
Решение.Запишем эти матрицы. Если первую разбить на строки, а вторую на столбцы, то видно, что есть всего 4 варината скалярно умножить друг на друга вектор-строку их первой на вектор-столбец из второй.

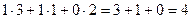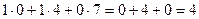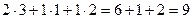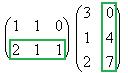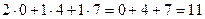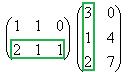
Например, если умножаем строку номер 1 на столбец номер 2, то и число, которое при этом получается, ставим в 1 строку 2 столбец новой матрицы. Итак,

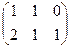
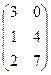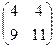= . Ответ. .

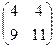Задача 2. Даны матрицы

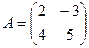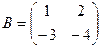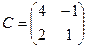, , . Найти .

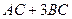Решение. Так как матрица С находится справа во всех слагаемых, то для удобства можно использовать приведение подобных 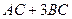= 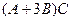- тогда умножение надо будет проводить всего один раз, а не два.

Сначала запишем .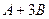

= = .

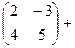
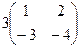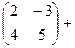
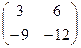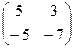Теперь умножим на матрицу С. Точно так же, как и в прошлом примере, мысленно обведём строку из 1-й матрицы на столбец из 2-й.

Есть 4 варианта это сделать:

= = = .

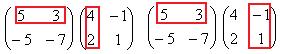
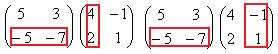
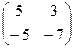
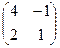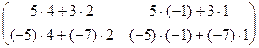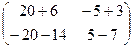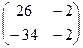Ответ. .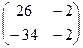

Задача 3. Дана матрица 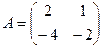найти .

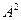Решение. Умножим матрицу саму на себя, то есть две её копии напишем рядом и умножим их.

= =

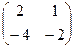
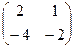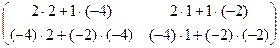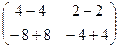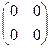= . Ответ. .

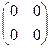Как видно из этого примера, для матриц, в отличие от чисел, возможно, что получается нулевой объект в ответе, притом что в исходной матрице вообще ни одного нуля не было. Это из-за особенностей её строения: правый столбец в 2 раза меньше, чем левый, а нижняя строка в минус 2 раза больше, чем верхняя. И вообще, если взять пару матриц, где у первой будет пропорциональность строк (в k раз больше) а у второй - столбцов (в минус k раз меньше) получим такой же эффект.

Домашняя задача №1.

Найти произведение матриц .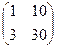

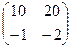Ответом здесь тоже будет служить нулевая матрица.

Задача 4. Даны матрицы 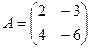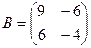. Найти .

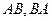Решение. = = .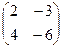

= = .

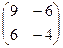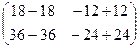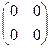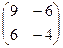
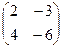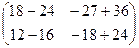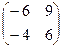Ответ. .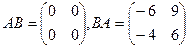

Задача 5. Даны матрицы:

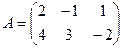
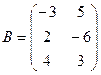Найти .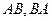

Решение.

= = .

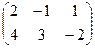
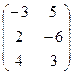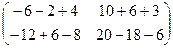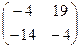Теперь поставим их наоборот, но при этом произведением будет уже не матрица 2 порядка, а матрица 3 порядка: теперь у первой 3 строки, но более коротких, а у второй 3 столбца. Вариантов умножить строку на столбец будет 9.

= = .

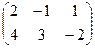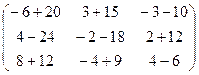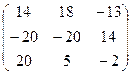Ответ. , .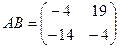

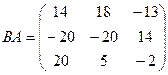Задача 6. Даны матрицы 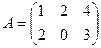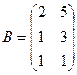. Найти .

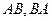Решение.

= = .

= = .

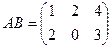
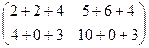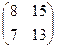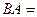
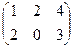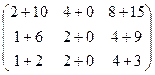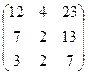Ответ. , .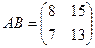

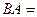
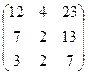Задача 7. Дана матрица 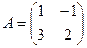. Найти .

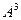Решение. Сначала умножим две, и найдём .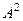

= = .

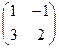
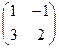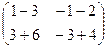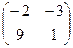Теперь домножим ещё на одну матрицу А, чтобы найти .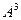

= = .

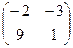
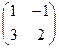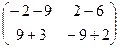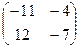Ответ. .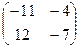

Домашняя задача № 2. Найти 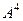для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить 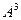, полученную в прошлой задаче, ещё раз на 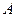, либо взять 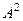, полученную на первом этапе, и её умножить саму на себя. Ответ. .

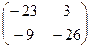Задача 8. Вычислить матрицу 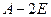для какой-нибудь матрицы 3-го порядка. (Операции типа 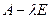понадобятся изучении следующих тем: собственные числа линейного оператора).

= =

= .

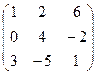
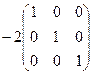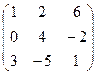
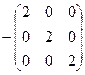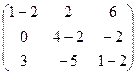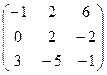Задача 9. Решить уравнение 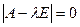для матрицы .

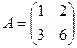Решение. = .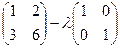

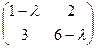Найдём определитель 2 порядка.

= .

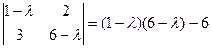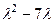Уравнение 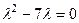, что равно 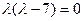, имеет 2 корня 0 и 7.

Ответ. Параметр 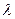может принимать значения 0 и 7.

Замечание. Фактически, здесь мы нашли все такие числа, что если их вычесть из главной диагонали, то строки будут пропорциональны. Одно из них 0 только потому, что строки и так изначально пропорциональны, т.е. можно вычесть 0. А если вычесть 7, получим:

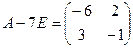тоже как строки, так и столбцы пропорциональны. Никакого третьего числа, обладающего таким свойством, для матриц 2 порядка нет, так как соответствующее уравнение (в будущем будем называть его характеристическим уравнением) 2 степени, и количество корней максимум 2. А вот для матрицы 3 порядка могло быть и 3 корня.

Задача 10. Найти определитель .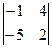

Решение. = .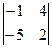

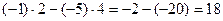Ответ. 18.

Замечание. Если построить пару векторов в плоскости, то площадь получившегося параллелограмма будет 18.

Задача 11. Найти определитель .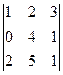

Решение.Допишем копии первых двух столбцов, проведём 3 параллельных линии (главная диагональ и ещё две). Перемножим все эти тройки элементов и внесём в общую сумму с их исходным знаком. А вот для побочной диагонали и линий, ей параллельных, со сменой знака.

=

.

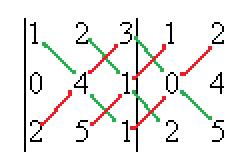
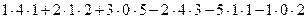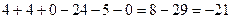Ответ. .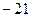

Замечание. Модуль этой величины равен объёму параллелепипеда, построенного на 3 векторах, если в качестве векторов рассматривать строки либо столбцы.

Так, эквивалентная формулировка этой задачи может быть: найти объём параллелепипеда, одна из верших которого (0,0,0), и 3 ребра расположены по радиус-векторам (1,0,2), (2,4,5), (3,1,1). Ответ: 21.

Если надо найти объём тетраэдра, то дополнительно разделить на 6.

Найти объём тетраэдра с вершинами (0,0,0), (1,0,2), (2,4,5), (3,1,1).

Ответ: 21 / 6 = 3,5. Дело в том, что площадь основания тетраэдра в 2 раза меньше, чем для параллелепипеда, а кроме того, в формуле объёма таких фигур, как пирамида, конус, тетраэдр есть коэффициент 1/3, итого в 6 раз меньше, чем для параллелепипеда.

Задача 12. Найти определитель .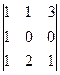

Решение проводится аналогичным образом,

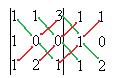
То, что перемножено по зелёным линиям, включим в сумму со знаком плюс, а по красным - со знаком минус.

= .

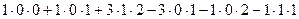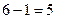Ответ. 5.

Задача 13. Найти определитель .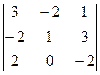

Решение.

.

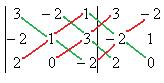
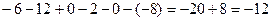Ответ. .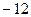

Задача 14. Найти определитель .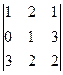

Решение.

.

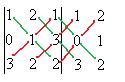
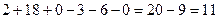Ответ. 11.