Основные понятия теории вероятностей

ОСНОВЫ

ТЕОРИИ ВЕРОЯТНОСТЕЙ

Методическое пособие для студентов - заочников

Великое множество событий совершается в окружающем нас мире. События взаимосвязаны – одни из них являются следствием (исходом) других и, в свою очередь, служат причиной третьих. Вглядываясь в гигантский водоворот взаимосвязанных явлений, можно сделать два важных вывода. Во-первых, наряду с совершенно определенными, однозначными исходами встречаются неоднозначные. Если первые можно предсказать точно, то вторые допускают лишь вероятные предсказания. Во-вторых, неоднозначные исходы встречаются чаще чем однозначные.

Вы нажимаете кнопку настольной лампы, и она зажигается. Здесь второе событие (загорелась лампа) является однозначным исходом первого события (нажата кнопка). Такое событие называется строго детерминированным. Другой пример: вы подбрасываете игральный кубик, на разных гранях которого изображены различные числа; и кубик падает так, что на верхней грани оказывается 4 очка. В данном случае второе событие (выпала четверка) уже не является однозначным исходом первого события (подброшен кубик). Ведь могло выпасть любое число от 1 до 6. Выпадение того или иного числа очков есть пример случайного события. Из приведенных примеров хорошо видно различие между строго детерминированными и случайными событиями.

Со случайными событиями (и вообще со случайностями разного рода) мы встречаемся очень часто, значительно чаще, чем это обычно принято считать. Случаен результат встречи двух спортивных команд одного и того же уровня подготовки, количество солнечных дней в данной местности изменяется от года к году случайным образом .

Совокупность случайных факторов лежит в основе любого процесса массового обслуживания – торговли, телефонной связи, транспорта, медицинской помощи и т . д .

ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ НАВЫКОВ К ЗАЧЕТУ

1. Студент должен уметь решать задачи:

· на вычисление вероятности случайного события по классическому, статистическому и геометрическому определению;

· на вычисление вероятности случайного события с использованием теорем суммы, произведения и полной вероятности;

· на вычисление вероятности по формулам Байеса, Бернулли, Муавра -Лапласа, Пуассона;

· на нахождение законов распределения и числовых характеристик дискретных и непрерывных случайных величин;

· на закон нормального распределения Гаусса.

ТЕОРИИ СЛУЧАЙНЫХ СОБЫТИЙ

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

1.Испытанием или опытом в теории вероятностей называется любая совокупность условий, которая может без изменения повторяться сколько угодно большое число раз.

2.Результат испытания называется исходом.

3.Исход, интересующий нас в данном испытании называется событием.

Для обозначения событий используют заглавные (прописные) буквы латинского, реже русского, алфавита.

Пример 1:

Испытание: бросание игральной кости (кубика с пронумерованными от 1 до 6 очков гранями).

Всевозможные исходы этого испытания:

· Появление 1 очка на верхней грани;

· Появление 2 очков на верхней грани;

· Появление 3 очков на верхней грани;

· Появление 4 очков на верхней грани;

· Появление 5 очков на верхней грани;

· Появление 6 очков на верхней грани.

Событие А₁ - появление 1 очка на верхней грани;

Событие А₂ - появление 2 очков на верхней грани;

Событие А₃ - появление 3 очков на верхней грани;

Событие А₄ - появление 4 очков на верхней грани;

Событие А₅ - появление 5 очков на верхней грани;

Событие А₆ - появление 6 очков на верхней грани;

Событие В - появление четного числа очков на верхней грани;

Событие С - появление нечетного числа очков на верхней грани;

Событие D - появление 4 очков на верхней грани и т.п.

4. Классическое определение вероятности.

Вероятностью события называется отношение числа исходов, в которых может появиться данное событие (благоприятных для появления события), к общему числу всевозможных исходов испытания.

Вероятность события обозначается прописной латинской буквой Р с указанием в скобках обозначения события, например: вероятность события А – Р(А), число всевозможных исходов испытания обозначается буквой n, а число благоприятных исходов – буквой m или, конкретизируя какому именно событию благоприятствуют данные исходы, - m_А, значение (величина) вероятности обозначается строчной латинской буквой p.

,

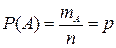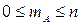
Пример 2:

· При бросании кубика (смотри пример 1) появлению события А будет благоприятствовать один исход (m=1) из 6 возможных (n=6), значит вероятность этого события будет равна ;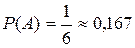

· Появлению события В будут благоприятствовать 3 исхода (m=3) из 6 возможных, т.е. благоприятными будут исходы с появлением четных цифр 2, 4, 6, значит вероятность появления этого события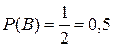

5. Событие называется случайным, если оно может появиться или не появиться в результате данного испытания. Если событие обязательно происходит в каждом исходе данного испытания, оно называется достоверным событием, если же событие не может произойти ни при одном исходе – оно называется невозможным.

6. Событие называется противоположным данному событию, если в результате испытания могут произойти только эти два события и они не могут появиться одновременно. Событие, противоположное данному событию А обозначается той же самой буквой, но с чертой над ней: 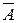, значение вероятности противоположного события .

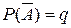Пример 3:

При бросании монеты возможны два события:

· Событие А – появление «орла»;

· Событие В – появление «решки» или, иначе, не появление «орла».

Значит событие В можно считать противоположным событию А, т.е. .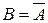

7. Основные свойства вероятности:

· Вероятность случайного события является неотрицательным числом и не превышает единицы: 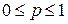, т.к. .

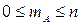· Вероятность достоверного события равна единице: 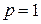, т.к. .

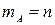· Вероятность невозможного события равна нулю: 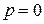, т.к. .

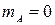· Сумма вероятностей данного и противоположного событий равна единице: .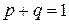

8. Два события называются равновозможными, если в результате опыта вероятности их появления равны.

9.Случайные события образуют полную группу, если при каждом испытании может осуществиться любое из них и не может осуществиться событие несовместимое с ним.

Пример 4.

· Выпадение ‘орла’ или ‘решки’ при бросании монеты один раз.

· Выпадение 1,2,3,4,5 или 6 очков при бросании кубика один раз.

События, образующие полную группу иногда называют элементарными событиями.

10. Два события называются совместными, если в результате опыта появление одного из них не противоречит появлению другого, т.е. они могут появиться одновременно. События, которые не могут ни при каких условиях появиться одновременно, т.е. появление одного из событий исключает появление другого, называются несовместными.

11. Два события называются зависимыми если вероятность появления одного из них зависит от того, произошло предварительно другое событие или нет, в противном случае, т.е. когда вероятность появления одного события не зависит от наступления другого, события называются независимыми.

Вероятность наступления события А, которое зависит от события В, называетсяусловной вероятностью и обозначается .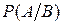

12. Суммой двух событий (А + В) называется событие С, которое заключается в наступлении по крайней мере (хотя бы) одного из этих событий, т.е. или первого, или второго, или обоих событий одновременно С = А + В = А или В.

13. Произведением двух событий (А * В) называется событие Д, которое заключается в одновременном наступлении обоих событий, т.е. и первого, и второго.