Неопределённость «бесконечность минус бесконечность»
Популярная неопределённость 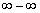 устраняется тремя распространёнными способами:
устраняется тремя распространёнными способами:
– приведением выражения под знаком предела к общему знаменателю;
– умножением/делением на сопряжённое выражение;
– преобразованием логарифмов.
Рассмотрим первый случай, о котором я ещё не рассказывал:
Пример 9
Вычислить предел
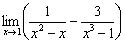
В данном пределе имеет место неопределённость 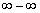 , и общий алгоритм решения незамысловат: необходимо привести выражение к общему знаменателю, а затем попытаться что-нибудь сократить:
, и общий алгоритм решения незамысловат: необходимо привести выражение к общему знаменателю, а затем попытаться что-нибудь сократить:
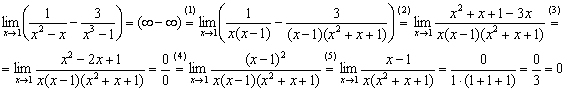
(1) Раскладываем знаменатели на множители: в первом знаменателе выносим «икс» за скобки, во втором знаменателе используем формулу разности кубов 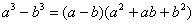 . Данный шаг можно было пропустить, но этим пришлось бы заниматься потом, и, на мой взгляд, разложение на множители удобнее провести сразу же.
. Данный шаг можно было пропустить, но этим пришлось бы заниматься потом, и, на мой взгляд, разложение на множители удобнее провести сразу же.
(2) Приводим выражение к общему знаменателю.
(3) Приводим подобные слагаемые в числителе. Неопределённость 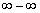 трансформировалась в неопределённость
трансформировалась в неопределённость 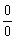 , которая стандартно раскрывается разложением числителя и знаменателя на множители.
, которая стандартно раскрывается разложением числителя и знаменателя на множители.
(4) Знаменатель уже разложен на множители. Раскладываем на множители числитель, в данном случае использована формула 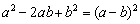 .
.
(5) Сокращаем числитель и знаменатель на 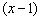 , устраняя неопределённость.
, устраняя неопределённость.
Как видите, новизны-то особой и нет.
Аналогичное задание для самостоятельного решения:
Пример 10
Вычислить предел
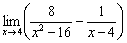
Решение и ответ в конце урока
Второй вид пределов с неопределённостью неопределённость 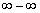 представляет собой разность, в которой присутствуют два или один корень:
представляет собой разность, в которой присутствуют два или один корень:
Пример 11
Вычислить предел
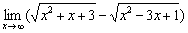
Каноничный образец. Метод решения подробно разобран на уроке Пределы. Примеры решений. Необходимо умножить и разделить на сопряженное выражение, чтобы потом воспользоваться формулой 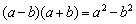
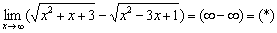
Умножим и разделим на сопряженное выражение:
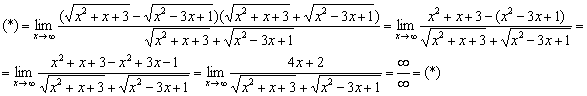
Неопределённость 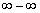 превратилась в неопределённость
превратилась в неопределённость 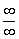 . Узнаёте? Такие семечки мы грызли в первом разделе данного урока.
. Узнаёте? Такие семечки мы грызли в первом разделе данного урока.
Числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу. Разделим числитель и знаменатель на 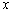 :
:
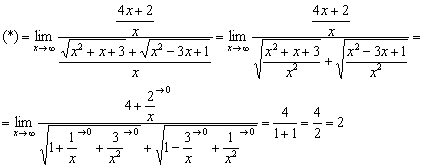
Не редкость, когда в разности всего один корень, но это не меняет алгоритма решения:
Пример 12
Вычислить предел
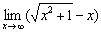
Пример 13
Вычислить предел
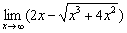
Это пара коротких примеров для самостоятельного решения.
Следует отметить, что пределы рассмотренного типа не обязаны равняться конечному числу, вполне может получиться и бесконечность, причём, как «плюс», так и «минус». Кстати, в примере №13 можно посмотреть на порядок роста членов, чтобы сразу выяснить ответ ;-)
Иногда на практике встречаются пределы-«обманки», в которых неопределённости «бесконечность минус бесконечность» нет вообще, вот простейший пример:
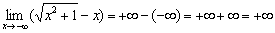
Таким образом, будьте предельно внимательны: перед решением предела необходимо убедиться, что неопределённость 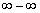 действительно есть!
действительно есть!
В заключительной части статьи вернёмся к незаслуженно забытым замечательным пределам, где рассмотрим, в том числе, третий тип пределов с неопределённостью 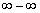 .
.
