Добротностью конденсатора и добротность катушки индуктивности
Катушка индуктивности - деталь, которая имеет спиральную обмотку и может концентрировать переменное магнитное поле. В отличие от резисторов и конденсаторов катушки индуктивности являются нестандартными радиодеталями и их конструкция определяется назначением конкретного устройства.
Основные параметры катушки индуктивности:
- Индуктивность
- Добротность катушки индуктивности
- Собственная ёмкость катушки индуктивности
- Температурная стабильность (температурный коэффициент)
Величина индуктивности прямо пропорциональна размерам катушки и количеству витков. Индуктивность также зависит от материала сердечника, введённого в катушку и наличия экрана. Расчёт катушки индуктивности выполняется с учётом этих факторов.
При введении в катушку сердечника из магнитных материалов (феррит, альсифер, карбонильное железо, магнетит) её индуктивность увеличивается. Это свойство позволяет уменьшить количество витков в катушке для получения требуемой индуктивности и тем самым уменьшить её габариты. Это особенно важно на низкочастотных диапазонах, когда нужна большая индуктивность. Погружая сердечник в катушку на разную глубину изменяют её индуктивность. Это свойство использовалось в старых радиоприёмниках при настройке на радиостанцию. В современных приборах наиболее часто это свойство используется в индуктивных бесконтактных датчиках. Такие датчики реагируют на приближение металлических предметов.
Влиять на индуктивность катушки можно и при отсутствии в ней подвижного сердечника. В этом случае одну из двух последовательно соединённых катушек помещают внутри другой. Если затем изменять её положение, то индуктивность также будет изменяться. Такая конструкция катушек называется вариометр.
Добротность катушки индуктивности – это качество работы катушки в цепях переменного тока. Добротность катушки индуктивности определяют как отношение её индуктивного сопротивления к активному сопротивлению. Грубо говоря,индуктивное сопротивление – это сопротивление катушки переменному току, а активное сопротивление – это сопротивление катушки постоянному току и сопротивление, обусловленное потерями электрической мощности в каркасе, сердечнике, экране и изоляции катушки. Чем меньше активное сопротивление, тем выше добротность катушки и её качество. Таким образом, можно сказать, что чем выше добротность, тем меньше потери энергии в катушке индуктивности.
Индуктивное сопротивление определяется формулой:
XL = ωL = 2πfL
Где ω = 2πf – круговая частота (f – частота, Гц); L – индуктивность катушки, Гн.
Добротность катушки индуктивности определяется формулой:
Q = XL / R = ωL / R = 2πfL / R
Где R – активное сопротивление катушки индуктивности, Ом.
36.Сущность символического метода расчета состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями, к алгебраическим уравнениям, составленным относительно комплексов тока и э. д. с. Этот переход основан на том, что в уравнении, составленном по законам Кирхгофа для установившегося процесса, мгновенное значение тока заменяют комплексной амплитудой тока. Мгновенное значение напряжения на активном сопротивлении uR = iR - комплексом 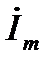 R, по фазе совпадающим с током. Мгновенное значение напряжения на индуктивности uL = L
R, по фазе совпадающим с током. Мгновенное значение напряжения на индуктивности uL = L 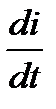 — комплексом j
— комплексом j 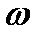 L
L 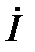 m, опережающим ток на 90°. Мгновенное значение напряжения на емкости uC=
m, опережающим ток на 90°. Мгновенное значение напряжения на емкости uC= 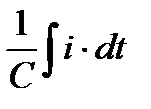 — комплексом
— комплексом 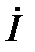 m
m 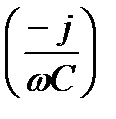 , отстающим от тока на 90о. Мгновенное значение э. д. с. е — комплексом
, отстающим от тока на 90о. Мгновенное значение э. д. с. е — комплексом 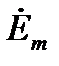 .
.
Рассмотрим пример расчета тока в схеме, приведенной на рис.
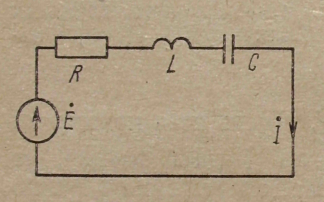
Уравнение для мгновенных значений можно записать так:
uR + uL + uC = e,
или
iR + L 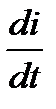 +
+ 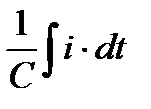 = e
= e
Запишем его в комплексной форме:
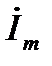 R + j
R + j 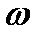 L
L 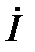 m +
m + 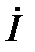 m
m 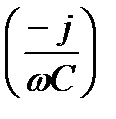 =
= 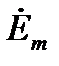 .
.
Решая это уравнение относительно 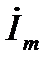 , получим:
, получим:
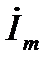 =
= 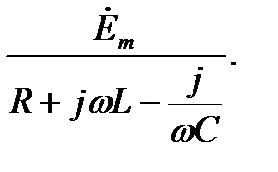
Метод называют символическим потому, что токи и напряжения заменяют их комплексными изображениями или символами. Так 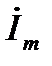 R — это изображение или символ падения напряжения iR; j
R — это изображение или символ падения напряжения iR; j 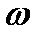 L
L 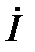 m - изображение или символ падения напряжения на индуктивности L
m - изображение или символ падения напряжения на индуктивности L 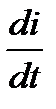 ;
; 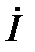 m
m 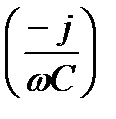 изображение падения напряжения на конденсаторе
изображение падения напряжения на конденсаторе 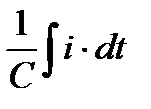 .
.
37.ВНИМАНИЕ! Ответ частично раскрыт в предыдущем вопросе+ (все формулы, данные тут, найдены в единичном варианте, так что за правильность не ручаюсь, но, к сожалению, больше ничего найти по этому вопросу не смог, поэтому рекомендую пользоваться формулами из предыдущего вопроса).
Если в электрической цепи действуют источники энергии, ЭДС и ток которых изменяется по гармоническому закону
ek(t) = Em*k S in(w t + y ek); Jk(t) = Jm*k Sin(w t + y jk ),
(Я так понимаю, что Em – это 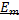 . Аналогично и для других, но я хз)
. Аналогично и для других, но я хз)
то токи и напряжения на всех участках этой цепи будут гармоническими функциями:
ik(t) = Im*k Sin(w t + y ik); uk(t) = Um*k Sin(w t + y uk),
где k – номер ветви или элемента. Далее будем полагать, что все источники одной цепи действуют с равной угловой частотой w .
Законы Кирхгофа справедливы для любых цепей и воздействий, в том числе и для цепей синусоидального тока.К примеру, определяя для схемы токи и напряжения, следует составить два уравнения:
i = i1+ i2 = Im*1 Sin(w t + y i1) + Im*2 Sin(w t + y i2);
uL = ur + uc = Um*r Sin(w t + y ur ) + Um*c Sin(w t +y uc).
Операции с гармоническими функциями в задачах электротехники принципиально проще выполнять, представив их комплексными числами. Такой метод называется символическим или методом комплексных чисел.
Переход от мгновенных значений к комплексным амплитудам производится следующим образом:
i = Im* Sin(w t + y i) соответствует Im = Im*ejy i,
u = Um* Sin(w t + y u ) соответствует Um = Um*ejy u,
38. Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора, подключённых к источнику напряжения. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
| I 1 |
| R2 |
| I2 |
| U2 |
| R1 |
| U1 |
| A |
Резистивный делитель напряжения служит для изменения уровня входного напряжения U1 в соответствии с формулой U2 = KU1, где K – коэффициент передачи делителя. Для нахождения Kсоставим уравнение по первому закону Кирхгофа для узла А в соответствии с выбранными направлениями токов:
I1 – I2 = 0
Подставим в это уравнение значения токов:
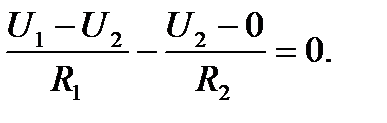
Представим уравнение в виде суммы слагаемых:
| U2 |
| I 1 |
| C |
| I2 |
| R |
| U1 |
| A |
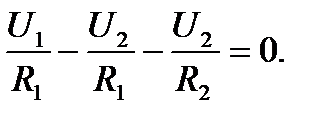
Перенесем в правую часть слагаемые с коэффициентами U2 и вынесем U2 за скобки:
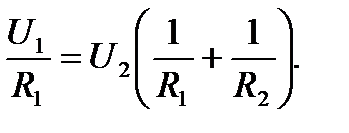
Приведем к общему знаменателю выражение в скобках:
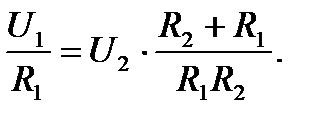
Найдем результат в виде отношения U2 / U1 :
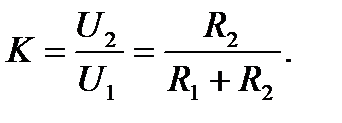
* Делитель напряжения может использоваться для усиления входного напряжения
* Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.
39. Фильтр нижних частот— электронный или любой другой фильтр, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты.
* Для звуковых волн твёрдый барьер играет роль фильтра нижних частот — например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине.
* Электронные фильтры нижних частот используются для подавления пульсаций напряжения на выходе выпрямителей переменного тока, для разделения частотных полос в акустических системах, в системах передачи данных для подавления высокочастотных помех и ограничения спектра сигнала, а также имеют большое число других применений.
* Радиопередатчики используют ФНЧ для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам.
* Механические низкочастотные фильтры часто используют в контурах АВМ непрерывных систем управления в качестве корректирующих звеньев.
* В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также при сжатии изображений.
40.
| U2 |
| I 1 |
| C |
| I2 |
| R |
| U1 |
| A |
Фильтр верхних частот (ФВЧ) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.
Простейший электронный фильтр верхних частот состоит из последовательно соединённых конденсатора и резистора. Конденсатор пропускает лишь переменный ток, а выходное напряжение снимается с резистора. Произведение сопротивления на ёмкость (R×C) является постоянной времени для такого фильтра, которая обратно пропорциональна частоте среза в герцах:
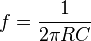
* Подобный фильтр используется для выделения высоких частот из сигнала и часто используется в обработке аудиосигналов, например в кроссоверах. Ещё одно важное применение фильтра верхних частот — устранение лишь постоянной составляющей, для чего частоту среза выбирают достаточно низкой.
* Фильтры верхних частот используются в простых бестрансформаторных конденсаторных преобразователях напряжения для понижения напряжения переменного тока. К недостаткам таких преобразователей относится их высокая чувствительность к импульсным помехам в источнике переменного тока, а также зависимость выходного напряжения от импеданса нагрузки.
* Фильтры верхних частот используются в обработке изображений для того, чтобы осуществлять преобразования в частотной области (например, для выделения границ).
* Используется также последовательное включение фильтра верхних частот с фильтром нижних частот (ФНЧ). Если при этом частота среза ФВЧ меньше, чем частота среза ФНЧ (то есть, имеется диапазон частот, в котором оба фильтра пропускают сигнал), получится полосовой фильтр (используется для выделения из сигнала определённой полосы частот).
41. ПолосовойRC - фильтр.
| Uвых |
| R2 |
| C2 |
| Uвх |
| R1 |
| C1 |
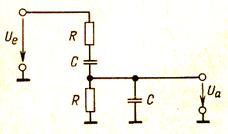
Рисунок 6.16 - Принципиальная схема полосового RC – фильтра
Рассчитаем выходное напряжение и фазовый сдвиг на средних частотах. Формула комплексного выходного напряжения для ненагруженного фильтра имеет вид
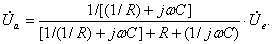
После преобразований, получим
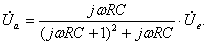
Обозначив 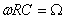 , получим комплексный коэффициент передачи
, получим комплексный коэффициент передачи
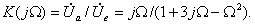
Выражение для коэффициента передачи по напряжению для полосового фильтра при R1=R2=R и C1=C2=C имеет вид
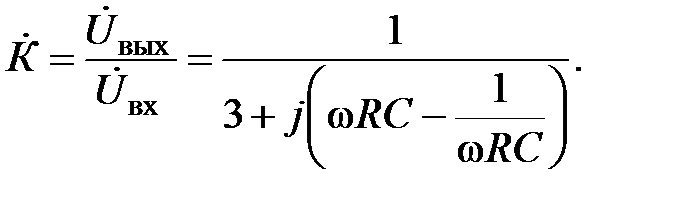 | (3.8) |
Из соотношения (3.8) для модуля коэффициента передачи (АЧХ) полосового фильтра следует:
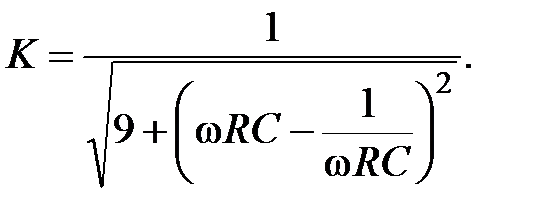
Максимальная величина модуля коэффициента передачи выражения (3.9) наблюдается при 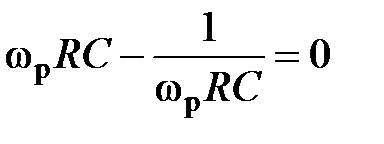 и принимает значение
и принимает значение
| Kp=1/3. | (3.10) |
График зависимости (3.9) показан на рис. 3.6. Как видно на данном рисунке, АЧХ полосового фильтра напоминает резонансную кривую колебательного контура. Поэтому соответствующую частоту 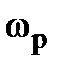 называют квазирезонансной. Ее значение может быть получено из выражения (3.9) с учетом соотношения (3.10)
называют квазирезонансной. Ее значение может быть получено из выражения (3.9) с учетом соотношения (3.10)
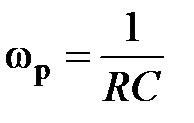 или или 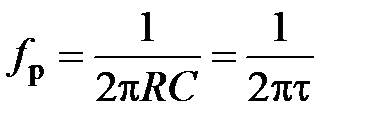 . . | (3.11) |
Отсюда найдем модуль и фазовый сдвиг
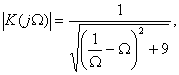
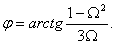
Выходное напряжение максимально при 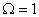 . Следовательно, резонансная частота равна
. Следовательно, резонансная частота равна 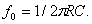 Величина
Величина 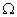 представляет собой нормированную частоту
представляет собой нормированную частоту 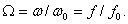 Фазовый сдвиг на резонансной частоте равен нулю, а коэффициент усиления равен 0,33. На рисунке 6.17 приведены графики зависимости коэффициента усиления и фазового сдвига от частоты.
Фазовый сдвиг на резонансной частоте равен нулю, а коэффициент усиления равен 0,33. На рисунке 6.17 приведены графики зависимости коэффициента усиления и фазового сдвига от частоты.
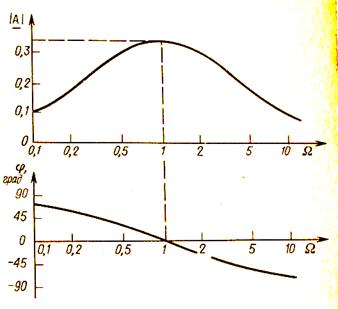
Рисунок 6.17 – Графики АЧХ и ФЧХ полосового фильтра
