Эффект Доплера для звуковых волн
Эффектом Доплера называют изменение частоты звука, воспринимаемой приемником при движении источника или приемника звука. Эффект легко «наблюдаем» в жизни. Достаточно вспомнить, как мимо вас с большой скоростью проносится пожарная машина с включенной сиреной. Мы слышим резкое изменение высоты тона этой сирены как только автомобиль проедет мимо нас.
Рассмотрим причины возникновения эффекта Доплера и вычислим изменение частоты звуковых волн, обусловленное этим эффектом.
Случай 1 – движется приемник звука вдоль прямой, соединяющей его с источником.
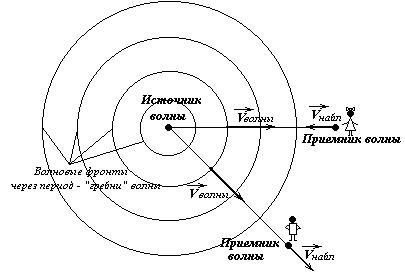
Пусть источник волны колеблется с частотой 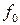 .
.
Очевидно, что расстояние между «гребнями», которое фиксирует приемник, не изменилось в сравнении с ситуацией, если бы приемник покоился. А вот приближаться к приемнику «гребни» волны будут с другой скоростью.
Если приемник приближается к источнику, то «гребни» двигаются относительно него со скоростью
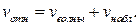
Выразим относительную скорость через длину волны и частоту, воспринимаемую приемником:
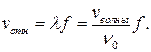 |
После подстановки получаем
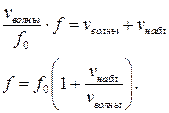
В случае удаления приемника звука от источника не трудно заметить, что в формуле для относительной скорости волны появится знак “-“, поэтому минус появится и в окончательном выражении для частоты, воспринимаемой приемником звука. Итак,
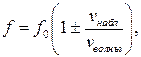
где знак “+“ для случая приближения приемника звука, знак “-“ для случая удаления приемника.
Проанализируем результат:
· в случае приближения приемника звука к источнику частота, воспринимаемая приемником, больше частоты волны, излучаемой источником;
· в случае удаления приемника звука от источника частота, воспринимаемая приемником, меньше частоты волны, излучаемой источником волны.
Случай 2 – движется источник звука вдоль прямой, соединяющей его с приемником.
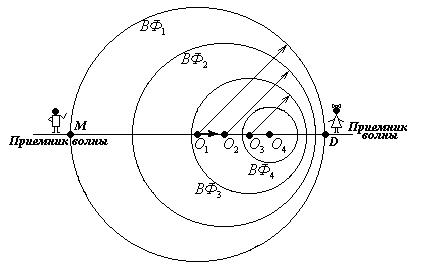
Пусть сирена продолжает испускать звук с частотой  . Автомобиль же «догоняет» испущенные им волны. Поэтому наблюдатель, стоящий у дороги, заметит, что при прежней скорости волны расстояния между «гребнями» стали короче – длина волны стала меньше.
. Автомобиль же «догоняет» испущенные им волны. Поэтому наблюдатель, стоящий у дороги, заметит, что при прежней скорости волны расстояния между «гребнями» стали короче – длина волны стала меньше.
С другой стороны, волны распространяющие позади автомобиля, будут дальше отстоять друг от друга, поскольку автомобиль как бы «отрывается» от них.
Пусть за время движения от О1 до О4 источник звука испустил N волн. Все они располагаются на отрезке
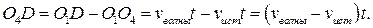 |
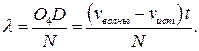 |
Расстояние между «гребнями» волн или длина волны будут равны
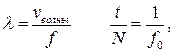 С учетом того, что
С учетом того, что
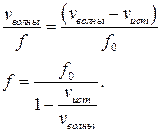 после подстановки получаем:
после подстановки получаем:
Видно, что наблюдатель, к которому источник звука приближается, слышит звук более высокой частоты или более высокого тона.
Для наблюдателя, стоящего позади удаляющегося автомобиля, рассуждения будут теми же самыми, с той лишь разницей, что испущенные источником волны будут лежать на отрезке О1М, что приведет к результату
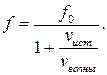
Для этого наблюдателя частота звука, испускаемого удаляющимся источником меньшей той, на которой он колеблется.
В общем случае движения источника звука можно записать
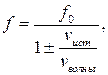
где верхний знак для случая удаления, нижний – приближения источника к приемнику звука.
Если звуковая волна отражается от движущегося препятствия, то частота отраженной волны будет отличаться от частоты падающей волны. Если же падающую и отраженную волну теперь наложить одна на другую, то возникнут биения. Такое проявление эффекта Доплера широко используется в медицинских приборах, использующих, как правило, ультразвуковые волны в мегагерцевом диапазоне частот. Например, отраженные от красных кровяных телец ультразвуковые волны можно использовать для определения скорости тока крови. Аналогичным образом можно осуществлять дистанционный контроль за сердцебиением, обнаруживать движение грудной клетки зародыша и т.д.
Следует отметить, что эффект Доплера лежит также в основе метода обнаружения с помощью радара автомобилей, которые превышают предписываемую скорость движения. Только в этом случае используются электромагнитные волны (радиоволны), а не звуковые.
Движение источника со сверхзвуковой скоростью
Если источник звуковой волны движется быстрее звука, то возникает более серьезный эффект, называемый ударной волной.
Пусть самолет, двигающийся со скоростью 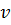 , превышающей скорость звука с, за время t переместился из точки О в точку S: OS =
, превышающей скорость звука с, за время t переместился из точки О в точку S: OS = 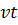 . Из каждой точки отрезка OS побежала сферическая звуковая волна. Огибающая сферических волн, испущенных из разных точек отрезка OS, представляет собой конус с вершиной на самолете (конус Маха). Угол раствора конуса равен
. Из каждой точки отрезка OS побежала сферическая звуковая волна. Огибающая сферических волн, испущенных из разных точек отрезка OS, представляет собой конус с вершиной на самолете (конус Маха). Угол раствора конуса равен 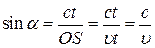 . Таким образом, самолет обгоняет издаваемый им звук.
. Таким образом, самолет обгоняет издаваемый им звук.
Волновой фронт каждой сферической волны – это область сгущения, т.е. область повышенного давления. Понятно, что в каждой точке поверхности конуса Маха давление воздуха будет превышать атмосферное. Это и есть ударная волна. Давление в ударной волне убывает по мере удаления от вершины конуса. Если самолет летит со сверхзвуковой скоростью на малой высоте, то человек, находящийся на земле, оказывается в области, близкой к вершине конуса Маха. Ударная волна проходит мимо человека за доли секунды, но он воспринимает ее как «акустический удар», который может привести к контузии.
§5 Примеры решения задач
Задача 1 Определение громкости звука по интенсивности волны
Интенсивность звуковой волны равна 7,5∙10-8 Вт/м2. Какова громкость звука, воспринимаемая человеком? Порог слышимости для среднего человека принять равным 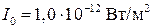 . Как изменится громкость звука, если интенсивность волны возрастет вдвое?
. Как изменится громкость звука, если интенсивность волны возрастет вдвое?
Решение:
1 Громкость звука определяется выражением 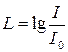 , где
, где 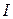 - интенсивность звуковой волны,
- интенсивность звуковой волны, 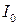 - порог слышимости – минимальная интенсивность волны, которая еще может вызывать слуховые ощущения у среднего человека.
- порог слышимости – минимальная интенсивность волны, которая еще может вызывать слуховые ощущения у среднего человека.
2 После подстановки получаем
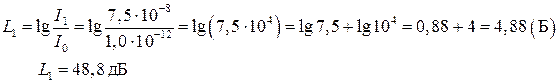
Такая громкость наблюдается при обычном негромком разговоре.
3 Если интенсивность звуковой волны возрастет вдвое, то
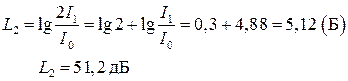
Важно заметить, что зависимость громкости звука от интенсивности волны не является линейной! Увеличение интенсивности волны в два раза приводит к увеличению громкости всего лишь на 3 дБ.
Задача 2 Максимальное смещение молекул воздуха в звуковой волне
Рассчитайте смещение молекул воздуха от положения равновесия в звуковой волне, интенсивность которой равна порогу слышимости 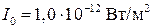 . Частота звука 1000 Гц, плотность воздуха при нормальных условиях 1,29 кг/м3, скорость звука при 0 0 С примерно равна 330 м/с.
. Частота звука 1000 Гц, плотность воздуха при нормальных условиях 1,29 кг/м3, скорость звука при 0 0 С примерно равна 330 м/с.
Решение:
1 Интенсивность звука в упругой среде равна 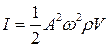 ,
,
где А – амплитуда колебания частиц; 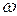 - циклическая частота колебаний частиц в волне;
- циклическая частота колебаний частиц в волне; 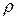 - плотность среды;
- плотность среды; 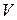 - скорость распространения волны в упругой среде.
- скорость распространения волны в упругой среде.
Интенсивность волны пропорциональна квадрату амплитуды колебания частиц!
2 Находим амплитуду колебания частиц в волне на пороге слышимости
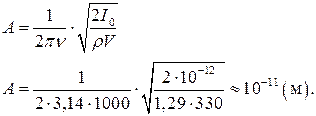
Полученный результат показывает, насколько чувствительно человеческое ухо – оно может улавливать перемещения молекул воздуха, меньшие размеров самих молекул ( 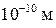 )!
)!
Задача 3 Колебания давления в звуковой волне на пороге слышимости и пороге болевых ощущений
Оцените колебания давления в звуковой волне на пороге слышимости и пороге болевых ощущений. Интенсивность волны на пороге слышимости равна 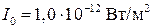 , громкость звука на пороге болевых ощущений равна 120 дБ, плотность воздуха при нормальных условиях 1,29 кг/м3, скорость звука при 0 0С примерно равна 330 м/с.
, громкость звука на пороге болевых ощущений равна 120 дБ, плотность воздуха при нормальных условиях 1,29 кг/м3, скорость звука при 0 0С примерно равна 330 м/с.
Решение:
Найдем связь между амплитудой колебания частиц и амплитудой колебания давления в звуковой волне.
1 По определению модуля всестороннего сжатия жидкостей или газов 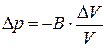 ,
,
где 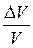 - относительное изменение объема газа, вызванное изменением давления
- относительное изменение объема газа, вызванное изменением давления 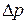 .
.
Знак «-» означает, что при расширении ( 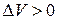 ) давление уменьшается (
) давление уменьшается ( 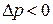 ).
).
2 Рассмотрим слой газа объемом V:
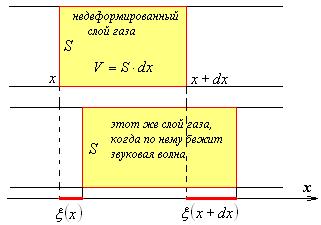
Изменение объема газа при смещении частиц в волне равно 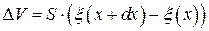 .
.
Относительное изменение объема газа равно
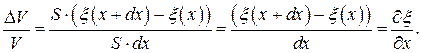
3 Подставляем найденное значение 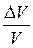 в выражение для расчета
в выражение для расчета 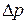 :
: 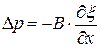 .
.
Смещение частиц определяется уравнением бегущей волны
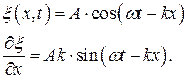
Изменение давления в звуковой волне с течением времени определяется выражением 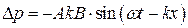 . Таким образом, звуковая волна представляет собой чередование областей повышенного и пониженного давления.
. Таким образом, звуковая волна представляет собой чередование областей повышенного и пониженного давления.
4 Амплитуда давления 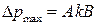 .
.
Выразим амплитуду колебания через интенсивность волны 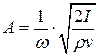 , заменим волновое число на
, заменим волновое число на 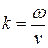 и скорость волны
и скорость волны 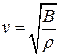 . После преобразования для амплитуды давления получим
. После преобразования для амплитуды давления получим 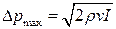 .
.
5 Амплитуда давления на пороге слышимости
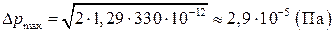 .
.
Удивительно!
6 Амплитуда давления на пороге болевых ощущений
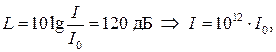
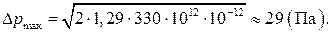
Задача 4 Громкость звука при одновременном звучании двух роялей
В концертном зале звучат два рояля одновременно. Громкость звучания первого L1 = 80 дБ, второго L2 = 70 дБ. Каков результирующий уровень громкости звука в зале?
1 Определяем интенсивность волны, испускаемой первым инструментом:
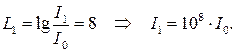
2 Определяем интенсивность волны, испускаемой вторым инструментом:
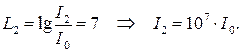
3 Результирующая интенсивность звука
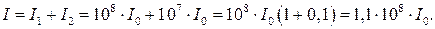
4 Результирующий уровень громкости
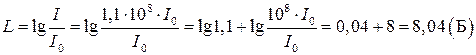 .
.
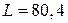 дБ.
дБ.
С точки зрения физики второй музыкант мог бы и не играть – его усилия не потревожат сон Васи Медведева, которого мама привела на концерт.
Задача 5 Движение приемника и источника звука
Основная частота звука сирены милицейского автомобиля, когда он стоит на месте, равна f0 = 1800 Гц. На какой частоте услышит звук сирены преступник, если он едет на угнанной «Оке» со скоростью v1 = 144 км/ч, а милицейский автомобиль двигается по встречной полосе со скоростью v2 = 54 км/ч? Скорость звука с = 343 м/с.
Решение:
1 Приближение автомобиля (источника волны) к преступнику приводит к увеличению частоты звуковой волны. Если бы преступник (приемник звука) не двигался, он слышал бы звук частоты 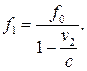 .
.
2 Движение приемника навстречу звуковой волне приводит еще к одному изменению воспринимаемой частоты:
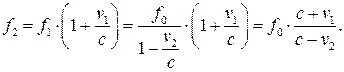
Преступник слышит звук 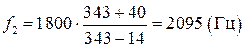 .
.
Задача 6 Звук двигателя самолета, движущегося со сверхзвуковой скоростью
Самолет летит горизонтально на высоте Н = 4 км над поверхностью земли со сверхзвуковой скоростью. Звук дошел до наблюдателя через время τ = 10c после того, как над ним пролетел самолет. Определите скорость v самолета. Скорость звука с = 330 м/с.
Решение:
1 Звуковая волна «тянется» за самолетом в виде конуса Маха с углом раствора 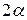 , где
, где 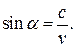
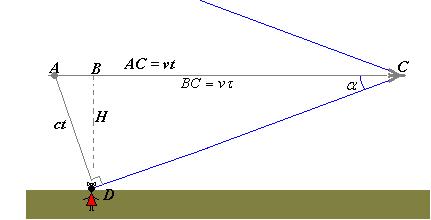
Сначала самолет пролетел над головой человека (прошел через точку В) только после этого, через время τ = 10 c, до человека дошел фронт звуковой волны. Звук, дошедший до человека, был испущен самолетов в точке А. За это время самолет из В переместился в С, пролетев расстояние СВ = vτ.
3 Рассмотрим подобные треугольники ACD и ВСВ:
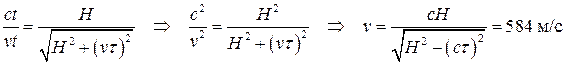
§6 Задания для самостоятельного решения
Тест « Звук»
1 Укажите формулу для расчета скорости звука в различных упругих средах
| Твердые тела | Жидкости | Газы |
А) 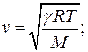 Б)
Б) 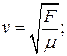 В)
В) 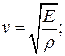 Г)
Г) 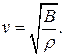
2 Задержка между моментом наблюдения молнии и звуком грома составила 5 с. Оцените, на каком расстоянии от наблюдателя идет гроза. Скорость звука при 20 0 С примерно 340 м/с.
А) 68 м; Б) 850 м; В) 1700 м; Г) 3400 м.
3 Оцените минимальное расстояние, на котором должна располагаться преграда, чтобы человек мог услышать эхо при отражении звука от нее. Ухо человека различает два звуковых сигнала, если время между их приходом составляет не менее 1/15 с. Скорость звука при 20 0 С примерно равна 340 м/с.
А) 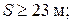 Б)
Б) 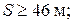 В)
В) 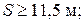 Г)
Г) 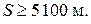
4 Установите соответствие между объективными и субъективными характеристиками звука.
| Объективная характеристика | Субъективная характеристика |
| Частота звуковой волны | |
| Набор частот в звуковой волне | |
| Интенсивность звуковой волны |
А) Громкость; Б) Тембр; В) Высота тона.
5 Громкость звучания TV увеличили от L1 = 30 дБ до L2 = 60 дБ. Во сколько раз увеличилась интенсивность звуковой волны 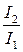 ?
?
А) 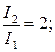 Б)
Б) 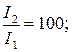 В)
В) 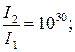 Г)
Г) 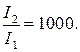
6 Уровень громкости от реактивного самолета на расстоянии 30 м от него равен L1 = 140 дБ. Каков уровень громкости от этого самолета на расстоянии 300 м? Отражением волны от земли пренебречь.
А) 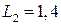 дБ; Б)
дБ; Б) 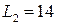 дБ; В)
дБ; В) 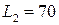 дБ; Г)
дБ; Г) 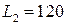 дБ.
дБ.
7 Звуковая волна переходит из одной упругой среды в другую. Что при этом происходит с характеристиками волны: скоростью, частотой, длиной волны?
А) Все три характеристики волны остаются неизменными;
Б) Все три характеристики меняются в зависимости от изменения среды;
В) Скорость и частота изменяются обратно пропорционально друг другу, длина волны остается неизменной;
Г) Скорость и длина волны изменяются прямо пропорционально друг другу, частота волны остается неизменной.
8 Составьте верное утверждение. Эффект Доплера – это явление…
А) Уменьшения амплитуды звуковой волны по мере удаления приемника от источника звука;
Б) Это явление изменения скорости и длины звуковой волны при переходе из одной среды в другую;
В) Это явление изменения частоты звуковой волны, воспринимаемой приемником, при относительном движении источника и приемника волны;
Г) Это явление наложения бегущей и отраженной волн с образованием стоячей волны.
9 Какая из приведенных формул правильно описывает эффект Доплера в случае движущегося наблюдателя и неподвижного источника звука? Скорость приемника звука 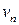 лежит на прямой, соединяющей источник и приемник волны. Скорость звука с.
лежит на прямой, соединяющей источник и приемник волны. Скорость звука с.
А) 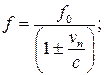 Б)
Б) 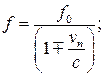 В)
В) 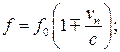 Г)
Г) 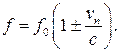
Примечание: верхние знаки в формулах для случая сближения, нижние – для случая удаления.
10 Какая из приведенных формул правильно описывает эффект Доплера в случае неподвижного наблюдателя и движущегося источника звука? Скорость источника звука 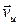 лежит на прямой, соединяющей источник и приемник волны. Скорость звука с.
лежит на прямой, соединяющей источник и приемник волны. Скорость звука с.
А) 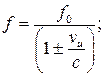 Б)
Б) 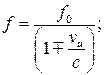 В)
В) 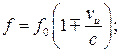 Г)
Г) 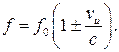
Примечание: верхние знаки в формуле для случая сближения, нижние – для случая удаления.
11 В неподвижном воздухе частота звука f0, скорость с, длина волны 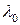 . Укажите причину того, что приближающийся к источнику звука приемник воспринимает волны, частота которой больше f0.
. Укажите причину того, что приближающийся к источнику звука приемник воспринимает волны, частота которой больше f0.
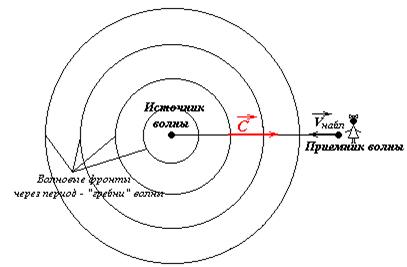
А) Для приближающегося приемника уменьшилось расстояние между гребнями воспринимаемой волны, то есть длина волны. Скорость же приближения гребней осталась неизменной. Из выражения 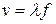 видим, что при неизменной скорости уменьшение длины волны приводит к увеличению частоты;
видим, что при неизменной скорости уменьшение длины волны приводит к увеличению частоты;
Б) Скорость сближения приемника и гребней волны увеличилась, а расстояние между гребнями (длина волны) не изменилась. Из выражения 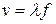 видим, что при неизменной длине волны увеличение скорости приводит к увеличению частоты.
видим, что при неизменной длине волны увеличение скорости приводит к увеличению частоты.
12 В неподвижном воздухе частота звука f0, скорость с, длина волны 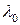 . Укажите причину того, что при приближении к приемнику источника звука приемник воспринимает волну, частота которой больше f0.
. Укажите причину того, что при приближении к приемнику источника звука приемник воспринимает волну, частота которой больше f0.
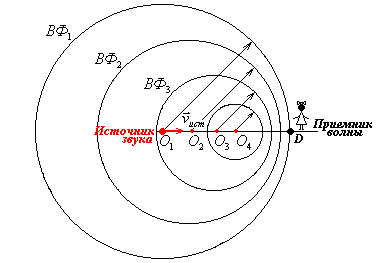
А) Для приближающегося приемника уменьшилось расстояние между гребнями воспринимаемой волны, то есть длина волны. Скорость же приближения гребней осталась неизменной. Из выражения 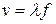 видим, что при неизменной скорости уменьшение длины волны приводит к увеличению частоты;
видим, что при неизменной скорости уменьшение длины волны приводит к увеличению частоты;
Б) Скорость сближения приемника и гребней волны увеличилась, а расстояние между гребнями (длина волны) не изменилась. Из выражения 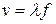 видим, что при неизменной длине волны увеличение скорости приводит к увеличению частоты.
видим, что при неизменной длине волны увеличение скорости приводит к увеличению частоты.
13 На рисунке показаны волновые поверхности через промежутки времени, равные периоду. Что можно сказать о движении источника звуковой волны в каждом случае?
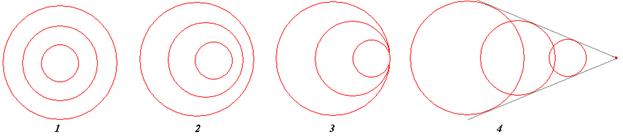
А) Источник звуковой волны двигается со скоростью 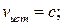
Б) Источник звуковой волны двигается со скоростью 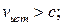
В) Источник звуковой волны двигается со скоростью 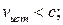
Г) Источник звуковой волны не двигается.
14 На рисунке показана звуковая волна, излучаемая самолетом. Угол 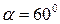 . С какой скоростью двигается самолет? Скорость звука принять равной 310 м/с.
. С какой скоростью двигается самолет? Скорость звука принять равной 310 м/с.
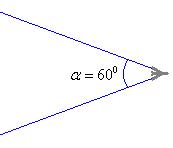
А) 105 м/с; Б) 268 м/с; В) 358 м/с; Г) 620 м/с.
Задачи
1 Вася Медведев наслаждается музыкой в клубе, где используется акустическая система Microlab PRO 1 Dark, выходная мощность которой 60 Вт. Регулятор громкости установлен в положение «max». Считая звуковую волну, излучаемую системой сферической и пренебрегая отражение звуковой волны от пола и стен, определите уровень громкости на расстоянии 3 м от динамика, где в это время блаженствует Вася. Интенсивность звуковой волны на пороге слышимости равна 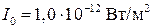 .
.
2 Оцените выходную мощность нормальной разговорной речи, считая, что звук распространяется приблизительно равномерно в полусфере вокруг рта человека. Громкость звука на расстоянии одного метра от говорящего равна 60 дБ. Интенсивность звуковой волны на пороге слышимости равна 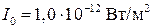 .
.
3 Во сколько раз изменится длина звуковой волны при переходе из воздуха в воду? Скорость звука в воздухе 340 м/с, в воде – 1480 м/с.
4 При какой интенсивности ультразвука в воде при атмосферном давлении начнется кавитация - появление микрополостей, разрывов в жидкости? Скорость ультразвука в воде 1480 м/с.
5 Одиночный комар, находящийся на расстоянии 10 м от человека, создает звук, близкий к порогу слышимости. Звук какой громкости создадут 1000 комаров?
6 Летучая мышь летит перпендикулярно к стене со скоростью v = 10 м/с, издавая ультразвук частотой f0 = 5∙104 Гц. Какую частоту f звуковой волны, отраженной от стенки, воспринимает мышь? Скорость звука примите равной с = 340 м/с.
7 Самолет летит горизонтально со скоростью v = 470 м/с. Человек услышал звук самолета через τ = 10c после того, как самолет пролетел над ним. Определите, на какой высоте летит самолет. Скорость звука с = 330 м/с.
Интерференция волн
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн по отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение носит название принципа суперпозиции волн.
В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, происходят с одной частотой и обладают постоянной во времени разностью фаз, волны называют когерентными.
При наложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.
Выясним, почему это происходит и каким условиям должны удовлетворять точки среды, чтобы в них наблюдалось усиление или гашение колебаний.
Пусть в некоторой области пространства распространяются две плоские волны одинаковой частоты w. Выясним, как будет вести себя произвольная точка Р среды, до которой доходят обе волны.
Согласно принципу суперпозиции точка Р должна прийти в два колебательных движения:
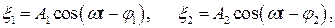 |
где j1 - запаздывание первой волны по фазе;
j2 - запаздывание второй волны по фазе.
Суммарное смещение точки Р будет равно
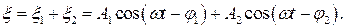 |
Складывать гармонические функции одной частоты удобно, используя метод векторных диаграмм.
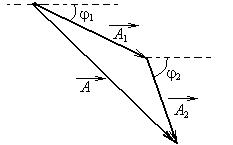
Амплитуда результирующего колебания А находится по теореме косинусов:
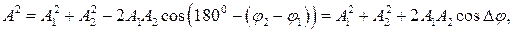 |
где Dj - разность фаз волн, приходящих в точку Р.
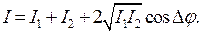 |
Поскольку интенсивность волны пропорциональна квадрату амплитуды, можно записать
Получили потрясающий результат!! Две волны приходят в точку, но энергия, приносимая в эту точку не равна сумме энергии каждой волны! Почему? Не нарушается ли здесь закон сохранения энергии?
Все дело в соsDj. Он может быть положительным – это будет означать, что энергия, приходящая к данную точку среды больше суммарной энергии двух волн. Колебания в этой точке усилились. Но ведь будут и такие точки среды, для которых соsDj отрицателен. Энергия, приходящая в эти точки, меньше суммарной энергии двух волн. Энергия двух волн просто перераспределилась между точками среды. За счет этого некоторые точки стали колебаться с большей амплитудой, а некоторые – с меньшей.
Очевидно, будут такие точки среды, для которых соsDj = 1. Энергия, приносимая волнами в эти точки, самая большая, они будут колебаться с максимально возможной амплитудой.
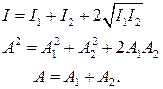
Говорят, что для таких точек выполняется условие максимума. Волны, приходящие в точку, должны быть синфазные, то есть Dj = 0, 2p, 4p,…
Если амплитуды волн одинаковы, то точки, для которых выполняется условие максимума, колеблются с амплитудой А = А1 + А1= 2А1, а энергия этих точек увеличивается в 4 раза в сравнении с тем, если бы точки совершали колебание в одной волне.
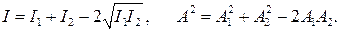 |
Найдутся такие точки среды, для которых соsDj = -1. Энергия, приходящая в эти точки, будет наименьшей, и колебаться эти точки будут с самой маленькой амплитудой.
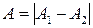 .
.
Говорят, что для таких точек выполняется условие минимума. Нетрудно видеть, что волны, приходящие в этом случае в точку, должны быть в противофазе, т.е. Dj = p, 3p,…
Если волны, приходящие в точку, для которой выполняется условие минимума, имеют одинаковые амплитуды, то, легко видеть, что I = 0 и А = 0. Точки просто не колеблются!!! Волны не просто ослабили друг друга, они полностью погасили друг друга.
Подведем некоторые итоги
1 В результате наложения когерентных волн наблюдается интерференционная картина – все точки среды колеблются, но амплитуды колебания точек разные. Эти амплитуды с течение времени не меняются, то есть картинка распределения амплитуд в пространстве остается неизменной. Говорят, что получилась устойчивая картина наложения. Устойчивая – не значит неподвижная! Все колеблются!
2 В некоторых точках среды волны усилили друг друга, точки колеблются с амплитудой, превышающей амплитуду каждой из волн в отдельности. Сюда поступает больше энергии.
3 Среди точек, в которых произошло усиление колебаний, можно выделить точки максимума – их амплитуда колебаний самая большая 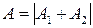 . Для того, чтобы в какой-либо точке выполнялось условие максимума, в нее должны приходить синфазные волны: Dj = 0, 2p, 4p,…
. Для того, чтобы в какой-либо точке выполнялось условие максимума, в нее должны приходить синфазные волны: Dj = 0, 2p, 4p,…
4 В некоторых точках среды волны будут ослаблять друг друга – амплитуда колебания точек будет меньше, чем в каждой из волн в отдельности. В эти точки поступает меньше энергии.
5 Среди точек, в которых произошло ослабление колебаний, выделяют точки минимума – амплитуда колебания этих точек самая маленькая 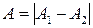 . В эти точки приходит самое маленькое количество энергии. В точках минимума может наблюдаться полное гашение колебаний, если амплитуды накладывающихся волн равны. В точки минимума волны должны приходить в противофазе: Dj = p, 3p,…
. В эти точки приходит самое маленькое количество энергии. В точках минимума может наблюдаться полное гашение колебаний, если амплитуды накладывающихся волн равны. В точки минимума волны должны приходить в противофазе: Dj = p, 3p,…
Осталось выяснить, откуда берется разность фаз волн, приходящих в какую-либо точку среды.
Во-первых, сами источники могут колебаться в разных фазах.
Во-вторых, расстояния, проходимые волнами, от источников до наблюдаемой точки, в общем случае разные.
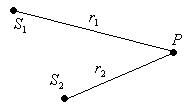
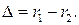 |
Разность расстояний от источников до рассматриваемой точки называется разностью хода волн
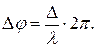 Разность хода дает разность фаз, которую несложно рассчитать через длину волны (пока мы рассматривает случай, когда волны распространяются в одной среде):
Разность хода дает разность фаз, которую несложно рассчитать через длину волны (пока мы рассматривает случай, когда волны распространяются в одной среде):
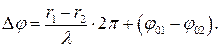 В общем случае разность фаз волн, приходящих в какую-либо точку среды, равна
В общем случае разность фаз волн, приходящих в какую-либо точку среды, равна
Все становится намного проще, если источники волн колеблются в одной фазе. Тогда разность фаз волн обусловлена только их разностью хода. В этом случае условия максимума и минимума можно сформулировать иначе.
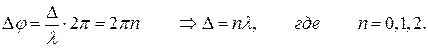 Для точек максимума на разности хода должно укладываться целое число длин волн:
Для точек максимума на разности хода должно укладываться целое число длин волн:
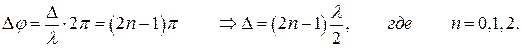 |
Для точек минимума на разности хода должно укладываться нечетное число полуволн:
Стоячие волны
Частным случаем интерференции является наложение падающей и отраженной волны, бегущей в противоположном направлении. Такое явление наблюдается, если дернуть за струну музыкального инструмента. По ней побежит волна, она отразится от точки закрепления струны, и мы будем наблюдать результат наложения падающей и отраженной волн.
Очень важный случай интерференции наблюдается при наложении встречных волн одной амплитуды. Исследуем эффект теоретически.
Уравнение бегущей волны
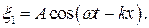
Уравнение встречной волны
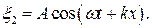
Результирующее колебание
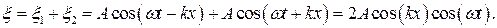
Нетрудно видеть, что в результате наложения двух встречных волн все точки колеблются с той же частотой w, что и встречные волны. Но вот амплитуды разных точек на оси ОХ, вдоль которой распространялись волны, разные.
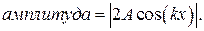 |
В точках, координаты которых удовлетворяют условию
 |
амплитуда колебаний достигает максимального значения 2А. Эти точки называются пучностями стоячей волны.
В точках, координаты которых удовлетворяют условию
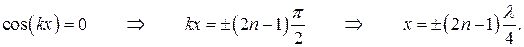 |
Амплитуда колебаний обращается в ноль. Эти точки называются узлами стоячей волны. Точки, находящиеся в узлах стоячей волны, колебаний не совершают!!!
Расстояние между соседними узлами, как и между соседними пучностями, равно l/2. Пучности и узлы сдвинуты относительно друг друга на четверть длины волны.
На рисунке показан ряд моментальных «фотографий» отклонения точек от положения равновесия в стоячей волне. Стрелками показаны скорости частиц.
Все точки, расположенные между двумя соседними узлами, колеблются в одной фазе: они одновременно проходят положение равновесия и одновременно приходят в положение максимального отклонения от положения равновесия.
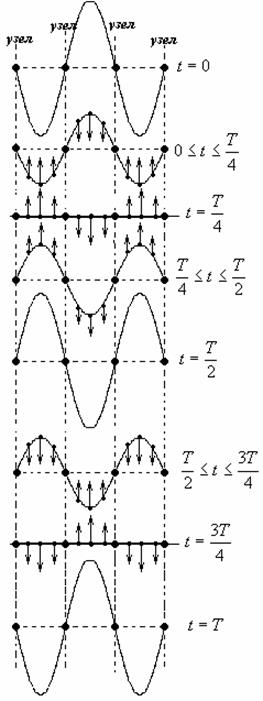 Видно, что точки по разные стороны от узлов колеблются в противофазе.
Видно, что точки по разные стороны от узлов колеблются в противофазе.
Почему стоячие волны столь важны в физике?
Вернемся к струне, закрепленной с двух сторон. При возбуждении колебаний в ней устанавливается стоячая волна. Причем в местах закрепления у этой волны должны располагаться узлы, ибо эти точки колебаться не могут. Поэтому в струне возбуждаются с заметной амплитудой только такие колебания, половина длины которых укладывается на длине струны целое число раз. Например, закрепленная струна может совершать следующие колебания:
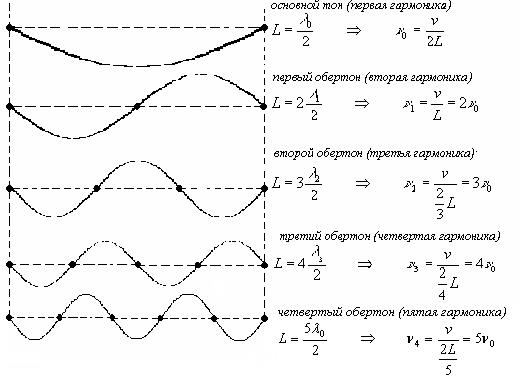
и т.д.
Частоты n0, n1, n2, n3 и т.д. называются для струны собственными частотами (или нормальными колебаниями). В общем случае колебания струны представляет собой наложение различных гармоник, т.е. струна одновременно участвует в нескольких собственных колебаниях.
Наибольшая амплитуда колебаний , как правило, будет на частоте основного тона. Чем выше номер гармоники, тем амплитуда колебаний будет меньше. Поэтому основной тон мы и слышим громче всего.
Важно!!
Струна в отличие от маятника имеет целый набор собственных частот колебаний! Сравните – маятник может совершать собственные колебания только с одной, собственной, частотой.
Любое тело подобно струне имеет набор собственных частот колебаний. Эти частоты соответствуют частотам стоячих волн, которые могут устанавливаться в теле. Очевидно, что собственные частоты или частоты стоячих волн будут зависеть от геометрических размеров и формы тела (они определяют длину волны), а также от вещества, из которого изготовлено тело (оно определяет скорость распространения волны в теле).
