Тема 6. Пределы и непрерывность

Предел числовой последовательности. Предел функции в бесконечности и точке. Бесконечно малые величины и их свойства. Бесконечно большие величины. Основные теоремы о пределах: теорема единственности, предел суммы, произведения, частного. Признаки существования предела. Второй замечательный предел. Число e. Понятие о натуральных логарифмах. Непрерывность функции в точке и на промежутке. Основные теоремы о непрерывных функциях. Раскрытие неопределенностей вида 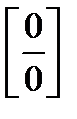, , 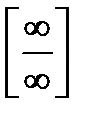, , 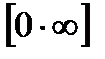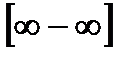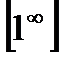. Вычисление пределов ([1 или 6, § 6.1 – 6.8]; [2 или 7, § 6.1 – 6.3, 6.5], или [3, § 6.1 – 6.10], или [5, §2.1 – 2.10]).

Наряду с понятием функции, понятия предела и непрерывности являются основными в разделе «Введение в анализ».

Понятие предела в учебнике [1, или 6, или 3] рассматривается для числовой последовательности 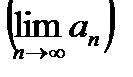и для функции: в бесконечности 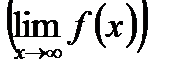и в точке 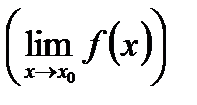. Для выяснения смысла этих понятий необходимо использовать их геометрическую интерпретацию. Весьма важными являются понятия бесконечно малых и бесконечно больших величин ([1, или 6, или 3, § 6.3, 6.4]), суть которых сводится к тому, что при своем изменении бесконечно малая (по абсолютной величине) будет меньше любого, как угодно малого числа 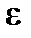> 0, а бесконечно большая будет больше любого как угодно большого числа М > 0.

Нужно знать взаимосвязь бесконечно малых и бесконечно больших величин, свойства бесконечно малых, с помощью которых доказываются теоремы о пределах. Следует обратить внимание на признаки существования пределов, особенно на теорему 1 ([1 или 6, или 3, § 6.5]), часто позволяющую установить наличие предела значительно проще, чем при использовании его определения.

Необходимо (без вывода) знать второй замечательный предел в двух формах запис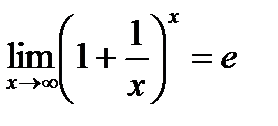и:

и .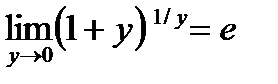

Понятие непрерывности функции (в точке, на промежутке) является более простым, чем предел, так как оно выражается непрерывностью графика при прохождении данной точки, данного промежутка (без отрыва карандаша от листа бумаги). Наряду с интуитивным представлением надо знать определение непрерывности функции в точке и на промежутке, свойства непрерывных функций, а также то, что всякая элементарная функция непрерывна в каждой точке области определения и может иметь разрыв лишь на границах области определения.

Раздел IV. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Тема 7. Производная

Задачи (о касательной к плоской кривой и о мгновенной скорости), приводящие к понятию производной. Производная, ее геометрический, механический и экономический смысл. Уравнение касательной к плоской кривой. Дифференцируемость функции. Связь между дифференцируемостью и непрерывностью функции (необходимый признак дифференцируемости). Основные правила и основные формулы дифференцирования. Формулы производных основных элементарных функций. Производная сложной функции. Техника дифференцирования. Производные высших порядков ([1 или 6, § 7.1 – 7.7]; [2 или 7, § 7.1 – 7.3], или [3, § 7.1 – 7.7, 7.11, 7.12], или [5, §3.1 – 3.7, 3.11, 3.12]).).

Студенты должны знать две классические задачи, которые приводят к понятию производной: задачу о касательной к плоской кривой и задачу о скорости неравномерного прямолинейного движения. Их решение выявляет геометрический и механический смысл производной. Нужно четко знать определение производной, представлять ее экономический смысл ([1или 6, § 7.6] или [3, § 7.10]), уметь составить уравнение касательной к графику любой функции y = f (x) в заданной точке.

Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует ее непрерывность в этой точке. Обратная теорема не справедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной ([1 или 6, § 7.2] или [3, § 7.2]).

Нужно, чтобы студенты, хорошо усвоив основные правила дифференцирования, умели находить производную суммы и произведения нескольких дифференцируемых функций, производную частного двух функций, пользоваться основными формулами дифференцирования, а также могли их вывести. Таблица основных формул приведена в учебнике ([1 или 6, или 3, § 7.5]) и на переднем форзаце. Наиболее важным для овладения техникой дифференцирования функций, и к тому же наиболее трудным, является правило дифференцирования сложной функции ([1, или 6, или 3, §7.4]). Знание этого правила способствует успешному освоению техники дифференцирования функций. Поэтому необходимо обратить особое внимание на примеры с решениями, в которых иллюстрируется его применение. Нужно усвоить понятия производных высших порядков и уметь их находить.