Свойства полугрупп и групп

Идемпотентом полугруппы G называется ее элемент i со свойством: i_*i=i. Множество всех идемпотентов полугруппы G обозначим E(G). Полугруппа G называется унипотентной, если ïE(G)ï=1.

Пусть G – полугруппа (группа), S – ее непустое подмножество. В силу ассоциативности полугрупповой (групповой) операции слово g₁…g_t длины t³1 в алфавите S не требует расстановки скобок, то есть является корректным. Если при этом g₁=…=g_t=g, то данное выражение записывают как g^t. Отсюда: g^tg^r=g^t+r, (g^t)^r=g^t×r. Для группы верны и следующие равенства: g⁰=е, g^-t=(g^-1)^t.

Для любого непустого подмножества S полугруппы G существует наименьшая подполугруппа в G, содержащая S, которая обозначается áSñ и состоит из всех конечных произведений элементов из S (иначе говоря, из всех конечных слов в алфавите S). Полугруппа áSñ коммутативна, если любая пара элементов из S коммутирует. Если S¢ - непустое подмножество обратимых элементов множества S, то áSñ - моноид и áS¢ñ - группа обратимых элементов моноида áSñ. В частности, если все элементы из S обратимы, то áSñ – группа.

Если S содержит только один элемент g, то полугруппа ágñ называется циклической или моногенной, а элемент g – порождающим циклическую полугруппу ágñ. Если элемент g обратим, то ágñ - циклическая группа. Если áSñ=G, то множество S называют порождающимG или системой образующих элементов полугруппы(группы) G.

Система образующих определена для полугруппы G в общем случае неоднозначно. Неоднозначной может быть и запись элемента g полугруппы G в виде слова в алфавите S.

Длиной элемента g конечной полугруппы в системе образующих S, обозначаемой l(g,S), называется длина кратчайшего из слов в алфавите S, представляющих элемент g.

Длиной покрытия непустого подмножества XÍG в системе образующих S, обозначаемой l(X,S), называют наибольшую из длин всех элементов множества X в системе образующих S:

l(X,S)= 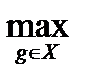l(g,S).

Графом Кэли Г_S полугруппы (группы) G=áSñ, построенным по системе образующихS, называют ориентированный граф с множеством вершин G и с множеством дуг, помеченных элементами системы S. Если g,g¢ÎG, sS, то (g,s,g¢) есть помеченная дуга Û g×s=g¢. Граф Г_S группы G является псевдосимметрическим графом порядка p, где p=ïSï.

Граф Кэли любой группы связен и не имеет параллельных дуг. В графе Кэли полугруппы могут существовать параллельные дуги. Граф Кэли полугруппы в общем случае не связен, он имеет не более ïSï компонент связности и любая вершина графа достижима хотя бы из одной вершины множества S. Например, граф Кэли полугруппы левых нулейпредставляет собой набор изолированных петель.

Возьмем элемент g полугруппы G и построим ряд элементов g,g²,…,gⁱ,… Если в ряду не встречаются одинаковые элементы, то полугруппы G и ágñ имеют бесконечные порядки.

Пусть в ряду g,g²,…,gⁱ,… встречаются одинаковые элементы (в случае конечной полугруппы G совпадения неизбежны), и t – наименьшее натуральное число такое, что g^d=g^t при некотором натуральном d<t. Обозначим n=t-d и перепишем последнее равенство в виде

g^d=g^d+n.(4.1)

Для конечной циклической полугруппы ágñ равенство (4.1) называют определяющим соотношением, а пару ág;g^d=g^d+nñ, состоящую из порождающего элемента g и определяющего соотношения - ее копредставлением. Из (4.1) следует, что равенство g^d+i=g^d+n+i выполнено при любом iÎN, т.е. полугруппа ágñ полностью задана копредставлением.

Число d называют циклической глубинойилииндексом элементаg (обозначается depg). Число n называют периодом элемента g(обозначается perg). Элемент g полугруппы с циклической глубиной d и с периодом n имеет тип (d,n) и порождает циклическую полугруппуágñ типа (d,n). Если для элемента g типа (d,n) верно соотношение g^d=g^d+n, то d³d и n|n.

Из соотношения (4.1) следует, что множество элементов полугруппы ágñ есть {g,g²,…,g^d+n-1}. Граф Кэли Г_g полугруппы ágñ состоит из единственного цикла длины n (множество C(g) циклических вершин графа есть {g^d,…,g^d+n-1}) и при d>1 из единственного подхода длины d-1 из вершины g к циклической вершине g^d (множество D(g) ациклических вершин графа есть {g,…,g^d-1}).

Порядком элемента g полугруппы G (обозначается ordg) называется наименьшее натуральное t такое, что g^t=e_g. Если g порождает циклическую полугруппу типа (d,n), то ordg=éd/nù×n. Отсюда ordg£ordágñ, и ordg=ordágñ Û n|(d-1) (длину подхода в Г_g).

Экспонентом полугруппы G (обозначается expG) называется наименьшее натуральное t такое, что g^t=e_g для любого gÎG [61]. Если G={g₁,…,g_m}, то

expG=НОК(ordg₁,…,ordg_m).

Отметим свойства циклических подполугрупп ágⁱñ полугруппы ágñ, i³1 [60].

Утверждение 4.1. а) При любых i,j ³1:

§ D(gⁱ)={g^k: k<d и k кратно i};

§ C(gⁱ)={g^k: d£k<d+n и kºt(modr)}, где t=ordg и r=(i,n);

§ полугруппа ágⁱñ определяется соотношением (gⁱ)^d=(gⁱ)^d+n, где d=éd/iù, n=n/(n,i);

б) ordgⁱ = ;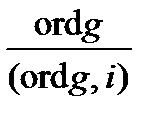

в) ágⁱñ=ág^jñ Û либо i=j, либо (i,n)=(j,n) при i,j³d;

г) ágⁱñÇág^jñ=ág^НОК(i,j)ñ. w

Не всякая подполугруппа циклической полугруппы является циклической.

Порядком элемента g группы (обозначается ordg) называется наименьшее натуральное t такое, что g^t=e. Экспонентом группы G, обозначаемой expG, называется наименьшее натуральное t (если такое существует), при котором g^t=е для всех gÎG.

Для элемента g конечного порядка t выполнены свойства:

1) t делит expG, и expG делит |G|, если G конечна;

2) g^п=е Û t|п;

3) элементы gⁱ и g^t-i являются взаимно обратными, i=0,1,…,t;

4) ordgⁱ=t/(t,i), i=1,…,t. w

В силу свойства 1 любая группа простого порядка p является циклической.

Теорема 4.3.Если элементы g и h группы G перестановочны и имеют порядки п и т соответственно, то в G найдётся элемент порядка НОК(п,т).

t Если (п,т)=1,то искомым элементом является g×h.

Действительно, элементы g и h перестановочны, поэтому (gh)^t=е при t=НОК(п,т). Отсюда ord(gh)=t, где t£t, при этом tït в соответствии со свойством 2). Значит, t=uv, где uïп, vïт. Заметим, число uт кратно t, поэтому (gh)^uт=е. Следовательно, используя перестановочность элементов g и h, имеем:

е=(gh)^uт=g^uт×h^uт=g^uт.

Отсюда в соответствии со свойством 2) число uт кратно п, что при (п,т)=1 верно Û u=п. Симметричным образом показывается, что v=т. Следовательно, t=t.

Если (п,т)=d,то ordg^d=п/d, и (п/d,т)=1. Как показано выше ord(g^dh)=пт/d=НОК(п,т). Искомый элемент есть g^dh. u

Следствие. В абелевой группе G имеется элемент g порядка expG. w

Бесконечная группа может состоять из элементов конечного порядка.

Теорема 4.4.Всякая подгруппа циклической группы - также циклическая.

t Пусть H – собственная подгруппа циклической группы ágñ. Из g^пÎH следует, что g^-пÎH, поэтому H содержит степени элемента g с натуральными показателями. Обозначим через d наименьшее натуральное число, для которого g^dÎH. Пусть теперь g^пÎH, где п=d×q+r, 0£r<d. Тогда g^r=g^п×(g^-d)^qÎH, что противоречит минимальности d, если r¹0. Поэтому r=0и H есть циклическая группа ág^dñ. u

Теорема 4.5. В конечной циклической группе ágñ порядка n элемент g^r порождает подгруппу порядка n/(r,n).

t Пусть d=(r,n). Порядок группы ág^rñ равен наименьшему натуральному t такому, что g^r×t=е. В соответствии со свойством 2) это равенство выполнено Û n делит r×t, то есть Û n/d делит t. Наименьшее натуральное t с таким свойством равно n/d. u

Пусть G – моноид, S,S¢ÍG и H£I_G. Элементы а,bÎG(подмножества S и S¢) называются сопряженными в группеH, при H=I_G просто сопряженными, если d^-1аd=b (d^-1Sd=S¢) для некоторого элемента dÎH. Обозначим отношение сопряженности а»^Hb (S»^HS¢) или а»b (S»S¢) при H=I_G. Для коммутативного моноида G сопряженность относительно любой группы H есть равенство.

Утверждение 4.3. При любой группе H отношение сопряженности »^H на моноиде G (на булеане 2^G моноида G), есть отношение эквивалентности.

t Если e – единица моноида G, то eÎH и выполнено:

1) а»^Hа, так как e^-1аe=а.

2) Если а»^Hb, то d^-1аd=b при некотором dÎH. Умножая последнее равенство слева на d и справа на d^-1, получаем: (d^-1)^-1bd^-1=а. По свойству группы d^-1ÎH, отсюда b»^Hа.

3) Если а»^Hb и b»^Hс, то d^-1аd=b и h^-1bh=с при некоторых d,hÎH. Подставляя во второе равенство вместо b левую часть первого равенства, получаем:

с=h^-1d^-1аdh=(dh)^-1а(dh).

Так как dhÎH, то это означает, что а»^Hс.

Для отношения сопряженности подмножеств доказательство аналогично. u

Утверждение 4.4. Если а»^Hb, где а,b - элементы моноида G, и элемент а имеет тип (d,n), то и элемент b имеет тип (d,n).

t По условию а^d=а^d+n, и d^-1аd=b при некотором gÎH. Отсюда

b^d=g^-1а^dg=d^-1а^d+nd=b^d+n.

Следовательно, если b имеет тип (d¢,n¢), то d¢£d и n¢|n. Рассуждая симметрично от элемента b к элементу а, получаем d£d¢ и n|n¢. Значит, d=d¢ и n=n¢. u

Следствие. Если а»^Hb, где а,b - элементы группы G, то ordа=ordb. w

Таким образом, разбиение моноида (группы) G на классы сопряженных элементов есть продолжение разбиения G на классы однотипных (однопорядковых) элементов.

Обозначим через [a]_» класс сопряженных элементов, содержащий элемент а моноида G. Определим ï[a]_»ï для аÎG.

Центром моноида(группы) G (обозначается C(G)) называется подмножество всех элементов G, перестановочных с любым элементом группы I_G (группы G). Отсюда:

1) C(G) – подмоноид моноида (подгруппа группы) G;

2) ï[a]_»ï=1 Û аÎC(G).

Нормализатором подмножества M моноида(группы) G, обозначаемым N_G(M), называется подмножество всех элементов g группы I_G (группы G), для которых gM=Mg. Отсюда

C(G)= 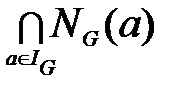(C(G)= ),

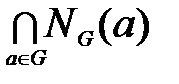где N_G(а)=N_G({а}) для любого аÎI_G (аÎG).

Теорема 4.10. Нормализатор подмножества M моноида G есть подгруппа в I_G. Для любого аÎG:

ï[a]_»ï=[I_G:N_G(а)].