Действительно, прямая АК пересекает прямую ВС и находится в пл.
перпендикулярной к прямой ВС', следовательно, AKLBC.
В 15 было показано (рис. 92), как можно провести перпендикуляр из
Точки на прямую. Но там это было выполнено при помощи введения в систему
Дополнительной плоскости и образования, таким образом, системы 3, 1,
В которой пл. 3 проводится параллельно заданной прямой. Рекомендуем
сравнить построения, данные на рис. 92 и 191,
На рис. 192 изображены плоскость общего положения о, проходящая через
Точку A, и перпендикуляр AM к этой плоскости, продолженный до пересечения с
пл. , в точке В'.
Угол 1 между пл. и пл. nt и угол между прямой AM и пл. являются
острыми углами прямоугольного треугольника В'AM', и, следовательно, 1 + =
90°. Аналогично, если пл. составляет с пл. 2 угол ?, а прямая AM,
перпендикулярная к о, составляет с пл. 2 угол , 2 + = 90°. Из этого,
Прежде всего, следует, что плоскость общего положения, которая должна
Составлять с пл. угол ,, а с пл. 2 угол 2, может быть построена, лишь
если 180° > 1 + 2>90°.
Действительно, складывая почленно + = 90° и 2 + = 90°, получим
1 + 2 + + = 180°, . е. + 2 < 180°, а так как + < 90°
(см. с. 33), 1 + 2 > 90°. Если взять :1 + 2 = 90°, то получится
профильно-проецирующая плоскость, а если взять , + 2 = 180°, то получится
Профильная плоскость, т. е. в обоих этих случаях плоскость не общего
Положения, а частного.
ПОСТРОЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ
Построение плоскости , перпендикулярной к плоскости о, может быть
произведено двумя путями: 1) пл. проводится через прямую, перпендикулярную
К пл. а; 2) пл. проводится перпендикулярно к прямой, лежащей в пл. ос или
Параллельной этой плоскости. Для получения единственного решения требуются
Дополнительные условия.
На рис. 193 показано построение плоскости, перпендикулярной к
Плоскости, заданной треугольником CDE. Дополнительным условием здесь служит
То, что искомая плоскость должна проходить через прямую АВ. Следовательно,
Искомая плоскость определяется прямой АВ и перпендикуляром к плоскости
Треугольника. Для проведения этого перпендикуляра к пл. CDE в ней взяты
Фрон-
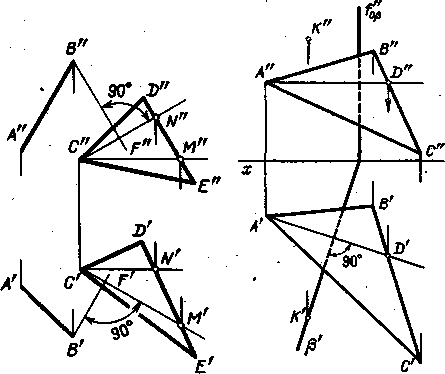
Рис. 193 Рис. 194
таль CN и горизонталь СМ: если B"F" % С" " и В'F'%С'М', то BF%пл. CDE.
Образованная пересекающимися прямыми А В и ВF плоскость перпендикулярна
к пл. CDE, так как проходит через перпендикуляр к этой плоскости. На рис.
Горизонтально-проецирующая плоскость проходит через точку К
Перпендикулярно к плоскости, заданной треугольником ABC. Здесь
Дополнительным условием явля-
лась перпендикулярность искомой плоскости сразу к двум плоскостям: к
Пл. ABC и к пл. ,. Поэтому и ответом служит горизонтально-проецирующая
Плоскость. А так как она проведена перпендикулярно к горизонтали AD, т. е. к
Прямой, принадлежащей пл. ABC, то пл. перпендикулярна к пл. ABC.
Может ли перпендикулярность одноименных следов плоскостей служить
признаком перпендикулярности самих плоскостей?
К очевидным случаям, когда это так, относится взаимная
Перпендикулярность двух горизонтально-проецирующих плоскостей, у которых
Горизонтальные следы взаимно перпендикулярны. Также это имеет место при
