Тема 6.1.Дискретная случайная величина.

Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.

Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы). Это множество может быть как конечным, так и бесконечным.

Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.

Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

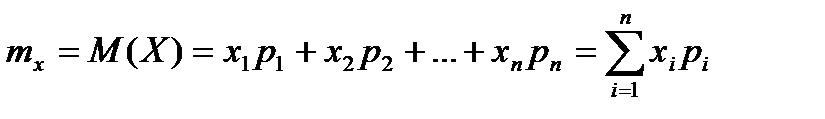
Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

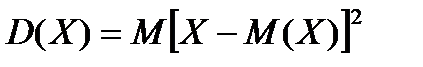
Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.

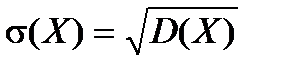
Контрольные вопросы:

1. Понятие случайной величины.

2. Приведите примеры дискретных и непрерывных случайных величин.

3. Чем отличаются дискретные случайные величины от непрерывных?

4. Когда можно сказать, что случайная величина задана?

5. Что называется законом распределения случайной величины.

6. Что называется рядом распределения и полигоном распределения для дискретной случайной величины.

7. Дайте определение функции распределения случайной величины. Ее свойства.

8. Дайте определение математического ожидания для дискретной случайной величины. В чем ее вероятностный смысл.

9. Дайте определение дисперсии для дискретной случайной величины. Запишите формулы, по которым вычисляется дисперсия дискретной случайной величины. В чем ее вероятностный смысл.

10. Дайте определение стандартного отклонения для дискретной случайной величины. В чем его вероятностный смысл.

11. Свойства числовых характеристик случайной величины – математического ожидания, дисперсии и стандартного отклонения.

Задание для контрольной работы

Контрольная работа состоит из 5 задачи согласно установленному варианту по следующим разделам и темам:

Раздел 1.Основы математического анализа

Тема 1.1. Теория пределов. Непрерывность ( вычисление пределов, раскрытие неопределенностей).

Тема 1.2. Дифференциальное исчисление функции одной переменной (дифференцирование, исследование функций и построение графиков).

Тема 1.3. Интегральное исчисление функции одной переменной (интегрирование непосредственным методом, методом замены переменной ; вычислением площади плоских фигур)