Тема 2. вступ до математичного аналізу
РОЗДІЛ IV: Функції
9. Знайти область визначення функцій:
1. 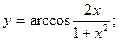
2. 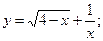
3. 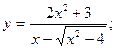
4. 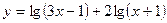 ;
;
10. Знайти множину значень функцій:
1. 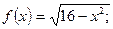
2. 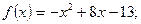
3. 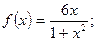
11. З’ясувати парність (непарність) функцій:
1. 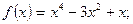
2. . 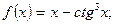
3. . 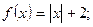
12. Знайти основні періоди функцій:
1. 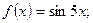
2. 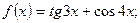
РОЗДІЛ V: Границя і неперервність
1). Довести, що при 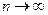 послідовність
послідовність 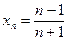 має границю число 1, починаючи з якого n абсолютна величина різниці між
має границю число 1, починаючи з якого n абсолютна величина різниці між 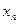 і 1 не перевищує
і 1 не перевищує 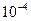 ?
?
2). Довести, що при 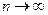 послідовність
послідовність 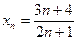 має границю число
має границю число 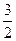 .
.
3). Довести, що при 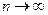 послідовність
послідовність 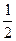 ;
; 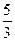 ;
; 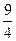
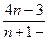 має границю, рівну 4.
має границю, рівну 4.
4). Довести, що при 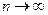 послідовність 1;
послідовність 1; 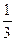 ;
; 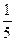 ;…..
;….. 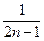 ……. є нескінченно малою.
……. є нескінченно малою.
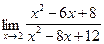 ;
; 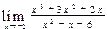

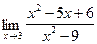 ;
; 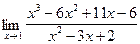
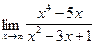 ;
; 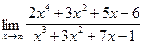
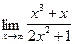
 ;
; 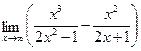
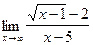 ;
; 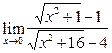
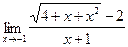 ;
; 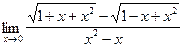
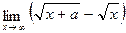 ;
; 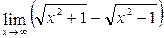
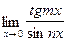 ;
; 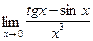
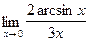 ;
; 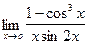
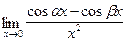 ;
; 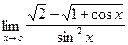
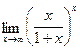 ;
; 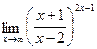
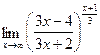 ;
; 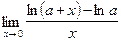
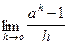 ;
; 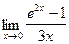
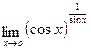 ;
; 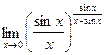
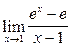 ;
; 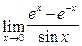

5). Показати, що при х=4 функція у= 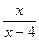
 має розрив.
має розрив.
6). Показати, що при х=5 функція у= 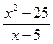 має розрив.
має розрив.
7). Знайти точки розриву функції 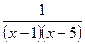
8). Які з даних функцій є неперервними в точці х=1?
Якщо є порушення неперервності, встановити характер точки розриву
у= 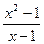 ; у=
; у= 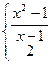 ,
, 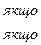
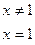 ;
;
у= 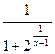 ; у=
; у= 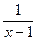 ;
;
ТЕМА ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
РОЗДІЛ VI: Похідні та диференціали
Знайти похідні функцій:
15) 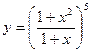 ; 16)
; 16) 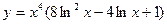 ;
;
17) 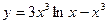 ; 18)
; 18) 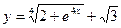 ;
;
19) 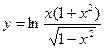 ; 20)
; 20) 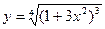 ;
;
21) 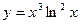 ; 22)
; 22) 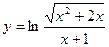 ;
;
23) 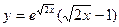 ; 24)
; 24) 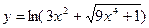 ;
;
25) 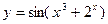 ; 26)
; 26) 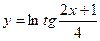 ;
;
27) 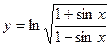 ; 28)
; 28) 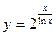 ;
;
29) 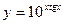 ; 30)
; 30) 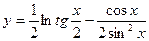 ;
;
31) 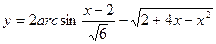 ; 32)
; 32) 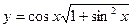 ;
;
33) 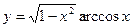 ; 34)
; 34) 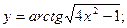
35) 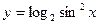 ; 36)
; 36) 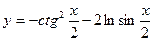 .
.
Знайти похідні функцій і обчислить їх значення при 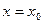 .
.
37) 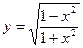 ;
; 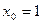 ; 38)
; 38) 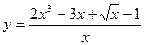 ;
; 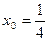 ;
;
39)  ;
; 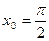 ; 40)
; 40) 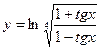 ;
; 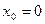 ;
;
41) Скласти рівняння дотичної до кривої 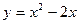
а) в точках перетину її з прямою 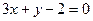 ;
;
б) паралельно і перпендикулярно цій прямій.
42) Знайти кут між кривими 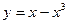 і прямою
і прямою 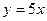 .
.
43) Тіло рухається прямолінійно по закону 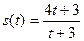 , де
, де 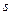 вимірюється в метрах, а t- в секундах. Знайти швидкість і прискорення тіла в момент
вимірюється в метрах, а t- в секундах. Знайти швидкість і прискорення тіла в момент 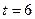 .
.
Знайти похідні від неявних функцій:
44) 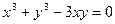 ; 45)
; 45) 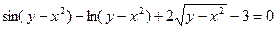 ;
;
46) 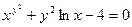 ; 47)
; 47) 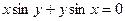 .
.
Знайти похідні від функцій заданих параметрично:
48) 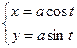 ; 49)
; 49) 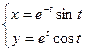 ;
;
50) Знайти приріст і диференціал функції 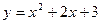 в точці
в точці 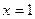 при
при 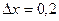 .
.
51) Обчислить приріст і диференціал функції 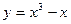 в точці
в точці 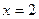 при
при
1) 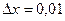 ;
;
2) 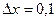 .
.
52) Знайти абсолютну похибку 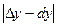 і відносну похибку
і відносну похибку 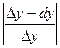 , які допускаються при заміні приросту функції її диференціалом.
, які допускаються при заміні приросту функції її диференціалом.
53) Знайти диференціал заданих функцій:
а) 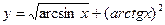 ;
;
б) 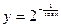 ;
;
в) 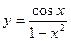 .
.
54) Використовуючи поняття диференціала, обчислити:
а) 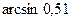 ;
;
б) 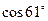 ;
; 
в) 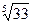 ;
;
г) 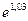 .
.
55) Використовуючи поняття диференціала, з'ясувати, з якою точністю повинен бути зміряний радіус круга, щоб його площу можна було визначить з точністю до 10%?
Використовуючи поняття диференціала, визначити, на скільки процентів зміниться величина степеня 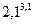 при зміні основи степеня на 5%.
при зміні основи степеня на 5%.
56) Обсяг продукції 
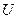 (ум.од.) цеху на протязі робочого дня представляє функцію
(ум.од.) цеху на протязі робочого дня представляє функцію
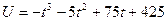 ,
,
де t - час (годинах). Знайти продуктивність праці через 2 год. після початку роботи.
57) Залежність між витратами виробництва y (грошові од.) і обсягом продукції, що виробляється x (од.), виражається функцією
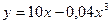 .
.
Визначить середні і граничні витрати при обсязі продукції, що дорівнює 5 од.
58) Функції попиту g і пропозиції s від ціни p виражаються відповідно рівняннями
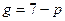 і
і 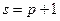 .
.
Знайти:
а) рівноважну ціну;
б) еластичність попиту і пропозиції для цієї ціни;
в) зміну доходу (в процентах) при підвищені ціни на 5% від рівноважної.
