Тема 1.1.5. Число элементов в объединении и разности конечных множеств(1ч.)
Нам известно, как находят объединение двух конечных непересекающихся множеств. Например, если А = {x,y,z}, а В = {k,l,m,p }, то Ах В = {х, у, z, к, I, т, р). Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?» -достаточно пересчитать их.
А как определять число элементов в объединении конечных множеств, не образуя его и не обращаясь к пересчету элементов?
Условимся предложение «Множество А содержит а элементов» записывать в таком виде: п(А) = а. Например, если А = {х, у, z}, то утверждение «Множество А содержит три элемента» можно записать так: п(А) = 3.
Если в множестве А содержится а элементов, а в множестве В - b элементов и множества А и В не пересекаются, то в объединении множеств А и В содержится а + b элементов, т.е.
п(А 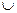 В)= n(A) +n(B)=a+b и если А = {x,y,z}, а В = {k,l,m,p }, то а+в=3+4=7
В)= n(A) +n(B)=a+b и если А = {x,y,z}, а В = {k,l,m,p }, то а+в=3+4=7
Это правило нахождения числа элементов в объединении двух конечных непересекающихся множеств.
1 пример: А = {х, у, г, р, /}, а В = {х, р, t}. Найдем число элементов в дополнении подмножества В до множества А.
Пересчитав элементы множеств А и В, получаем, что п(А) = 5, п(В) = 3. Тогда п(В'А) = п(А) - п{В) = 5-3 = 2. Таким образом, в дополнении множества В до множества А содержится два элемента.
Формула позволяет находить число элементов в объединении конечных непересекающихся множеств.
2 пример: А если множества А а В имеют общие элементы, то как найти число элементов в их объединении?
п(А 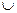 В) = п(А) + п(В) - п(А
В) = п(А) + п(В) - п(А 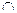 В)
В)
Пусть А={x,y,z}, а В = { k,у,х,m,p }, тогда : n(А 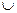 В)=6 , т.к. п(А) = 3, п(В) = 5 , n(А
В)=6 , т.к. п(А) = 3, п(В) = 5 , n(А 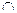 В)=2, и п(А
В)=2, и п(А 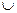 В) = п(А) + п(В) - п(А
В) = п(А) + п(В) - п(А 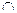 В)=3+5-2=6
В)=3+5-2=6
Если же мн-ва не пересекаются, то n(А 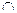 В)=0 и мы придем к формуле:
В)=0 и мы придем к формуле:
п(А 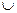 В)= n(A) +n(B)=a+b
В)= n(A) +n(B)=a+b
Задача: Из 40 студентов курса 32 изучают английский язык, 21 - немецкий язык, а 15 - английский и немецкий языки. Сколько студентов курса не изучает ни английский, ни немецкий языки?
Решение. Пусть А - множество студентов курса, изучающих английский язык, В - множество студентов курса, изучающих немецкий язык. По условию задачи: п(А) = 32 , п{В)= 21, п(А 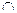 В) = 15. Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.
В) = 15. Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.
1 способ.
1) Найдем число элементов в объединении данных мно-
жеств А и В. Для этого воспользуемся формулой (2):
п(А 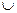 В)= п(А) + п(В) – п(А
В)= п(А) + п(В) – п(А 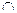 В) = 32 + 21 - 15 = 38.
В) = 32 + 21 - 15 = 38.
2) Найдем число студентов курса, которые не изучают ни английский, ни немецкий языки: 40 - 38 = 2.
2 способ.
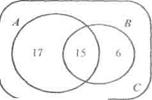
1) Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из непересекающихся подмножеств (рис.). Так как в
пересечении множеств А и В со держится 15 элементов, то студентов, изучающих только английский язык, будет 17 (32- 15 = 17), а студентов, изучающих только немецкий - 6 (21 - 15 = 6). Тогда п(А  В) = 17 + 15 + 6 = 38, и, следовательно, число студентов курса, которые не изучают ни английский, ни немецкий языки, будет 40 - 38 = 2.,т.к. n(С)=40
В) = 17 + 15 + 6 = 38, и, следовательно, число студентов курса, которые не изучают ни английский, ни немецкий языки, будет 40 - 38 = 2.,т.к. n(С)=40
Упражнения
1. Из 32 школьников 12 занимаются в волейбольной секции, 15 - в баскетбольной, 8 человек занимаются и в той, и в другой секции. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секции?
2. В третьем классе дети коллекционируют марки и монеты. Марки коллекционируют 8 человек, монеты - 5 человек. Всего коллекционеров 11. Объясните, как это может быть. Сколько человек коллекционируют только марки? только монеты?
3.Катя положила в коробку 4 зеленых круга, 6 треугольников и 3 красных многоугольника. Всего в коробке оказалось 11 фигурок. Сколько среди них красных треугольников?
Контрольная работа №1
