Упорядочение п наблюдений по мере возрастания перемен­ной х.

2. Исключение 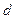средних наблюдений ( 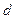должно быть примерно равно четверти общего количества наблюдений).

3. Разделение совокупности на две группы (соответственно с малыми и большими значениями фактора 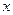) и определение по каждой из групп уравнений регрессии.

4. Определение остаточной суммы квадратов для первой регрессии 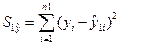и второй регрессии .

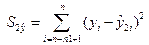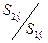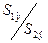5. Вычисление отношений (или ). В числителе должна быть большая сумма квадратов.

Полученное от­ношение имеет F распределение со степенями свободы k1=n1-k и k2=n-n1-k, (k– число оцениваемых параметров в уравнении регрессии).

Если 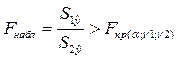, то гетероскедастичность имеет место.

Чем больше величина F превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточ­ных величин.

Оценка влияния отдельных факторов на зависимую переменную на основе модели (коэффициенты эластичности, b - коэффициенты).

Важную роль при оценке влияния факторов играют коэффициен­ты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени ко­леблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты b(j).

Эластичность Y по отношению к Х(j) определяется как процентное изменение Y, отнесенное к соответствующему процентному изменению Х. В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:

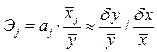
Эластичность ненормирована и может изменяться от - 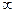до + 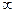. Важно, что она безразмерна, так что интерпретация эластичности 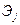=2.0 означает, что если 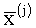изменится на 1%, то это приведет к изменению 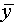на 2%. Если 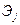=-0.5, то это означает, что увеличение 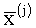на 1% приведет к уменьшению 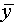на 0.5%.

Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную.

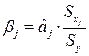
где S_xj — среднеквадратическое отклонение фактора j

где .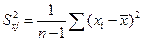

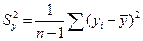Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент показывает, на какую часть величины средне­го квадратического отклонения S_y изменится зависи­мая переменная Y с изменением соответствующей независимой пере­менной Х_j на величину своего среднеквадратического отклонения при фиксирован­ном на постоянном уровне значении остальных независимых пере­менных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов мож­но оценить по величине дельта - коэффициентов D (j):

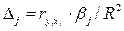
где 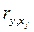— коэффициент парной корреляции между фактором j (j = 1,...,m) и зависимой переменной.