Рассмотрим выполнение предпосылки гомоскедастичности, или равноизменчивости случайной составляющей (возмущения).

Тема 4. Множественная регрессия.

Вопросы

1. Модель множественной регрессии. Оценка параметров множественной регрессии методом наименьших квадратов (МНК).

2. Предпосылки применения метода наименьших квадратов (МНК).

3. Свойства оценок метода наименьших квадратов (МНК).

4. Проверка качества многофакторных регрессионных моделей

5. Оценка существенности параметров линейной регрессии.

6. Мультиколлинеарность. Последствия мультиколлинеарности. Способы обнаружения мультиколлинеарности. Способы избавления от мультиколлинеарности.

7. Отбор факторов при построении множественной регрессии. Процедура пошагового отбора переменных.

8. Оценка влияния факторов на зависимую переменную (коэффициенты эластичности, бета коэффициенты).

9.Анализ экономических объектов и прогнозирование с помощью модели множественной регрессии.

Материал к этой лекции изложен в учебном пособии [1] на стр. 207 – 241.

Функция 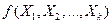, описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии[1]. Уравнение регрессии показывает ожидаемое значение зависимой переменной 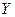при определенных значениях зависимых переменных .

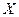В зависимости от количества включенных в модель факторов Х модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).

В зависимости от вида функции 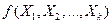модели делятся на линейные и нелинейные.

Модель множественной линейной регрессии имеет вид:

y _i = a₀ + a₁x _{i 1} +a₂x _{i 2} +…+ a_k x _{i k} + e_i 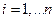(2.1)

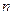- количество наблюдений.

коэффициент регрессии a_j показывает, на какую величину в среднем изменится результативный признак 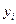, если переменную x_j увеличить на единицу измерения, т. е. a_j является нормативным коэффициентом.

Коэффициент 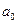может быть отрицательным. Это означает, что область существования показателя не включает нулевых значений параметров. Если же а0>0, то область существования показателя включает нулевые значения параметров, а сам коэффициент характеризует среднее значение показателя при отсутствии воздействий параметров.

Анализ уравнения (2.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи:

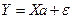(2.2) .

Где 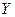– вектор зависимой переменной размерности п ´ 1, представляющий собой п наблюдений значений .

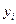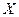- матрица п наблюдений независимых переменных 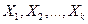, размерность матрицы 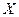равна п ´ (k+1) . Дополнительный фактор 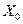, состоящий из единиц, вводится для вычисления свободного члена. В качестве исходных данных могут быть временные ряды или пространственная выборка.

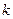- количество факторов, включенных в модель.

a — подлежащий оцениванию вектор неизвестных параметров размерности (k+1) ´ 1;

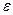— вектор случайных отклонений (возмущений) размерности п ´ 1. 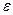отражает тот факт, что изменение 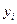будет неточно описываться изменением объясняющих переменных 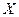, так как существуют и другие факторы, неучтенные в данной модели.

Таким образом,

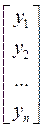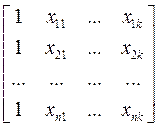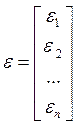Y = , X = , , a = .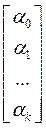

Уравнение (2.2) содержит значения неизвестных пара­метров a₀,a₁,a₂,… ,a_k . Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрес­сии, в которой вместо истинных значений параметров под­ставлены их оценки (а именно такие регрессии и приме­няются на практике), имеет вид

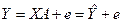, (2.3)

где A— вектор оценок параметров; е — вектор «оценен­ных» отклонений регрессии, остатки регрессии е = Y - ХА; 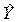—оценка значе­ний Y, равнаяХА.

Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов (МНК), суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

.

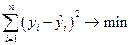Формулу для вычисления параметров регрессионного уравнения по методу наименьших квадратов приведем без вывода

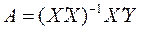(2.4).

Для того что­бы регрессионный анализ, основанный на обычном методе наименьших квад­ратов, давал наилучшие из всех возможных результаты, дол­жны выполняться следующие условия, известные как условия Гаусса – Маркова.

Первое условие. Математическое ожидание случайной составляющей в любом наблюдении должно быть равно нулю. Иногда случайная составляющая будет положительной, иногда отрицательной, но она не должна иметь систематичес­кого смещения ни в одном из двух возможных направлений.

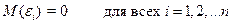
Фактически если уравнение регрессии включает постоянный член, то обыч­но это условие выполняется автоматичес­ки, так как роль константы состоит в определении любой систематической тенденции 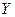, которую не учитывают объясняющие переменные, включен­ные в уравнение регрессии.

Второе условие означает, что дисперсия случайной составляющей должна быть постоянна для всех наблюдений.Иногда случайная составляющая будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы она по­рождала большую ошибку в одних наблюдениях, чем в других.

Эта постоянная дисперсия обычно обозначается 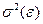, или часто в более крат­кой форме 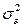, а условие записывается следующим образом:

.

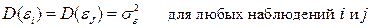Выполнимость данного условия называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью, (непостоянством дисперсии отклонений).

Третье условие предполагает отсутствие систематической связи между значени­ями случайной составляющейв любых двух наблюдениях. Например, если случайная составляющая велика и положительна в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что она будет большой и положительной в следующем наблюдении. Случайные составляющие должны быть независимы друг от друга.

В силу того, что 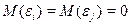, данное условие можно записать следую­щим образом:

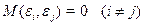
Возмущения 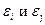не коррелированны (условие независимости случайных составляющих в различных наблюдениях).

Это условие означает, что отклонения регрессии (а значит, и сама зависимая переменная) не коррелируют. Условие некоррелируемости огра­ничительно, например, в случае временного ряда 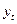. Тог­да третье условиеозначает отсутствие автокорреляции ряда .

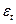Четвертое условие состоит в том, что в модели (2.1) возмущение 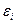(или зависимая переменная 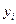) есть величина случайная, а объясняющая переменная 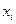- вели­чина неслучайная.

Если это условие выполнено, то теоретическая ковариация между независи­мой переменной и случайным членом равна нулю.

Наряду с условиями Гаусса— Маркова обычно также предполагается нормаль­ность распределения случайного члена.

В тех случаях, когда выполняются предпосылки, оценки, полученные по МНК, будут обладать свойствами несмещенности, состоятель­ности и эффективности.

Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблю­даемым данным проводится на основе анализа остатков - .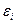

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.

Качество модели регрессии оценивается по следующим направлениям:

1) проверка качества всего уравнения регрессии;

2) проверка значимости всего уравнения регрессии;

3) проверка статистической значимости коэффициентов уравнения регрессии;

4) проверка выполнения предпосылок МНК.

При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом:

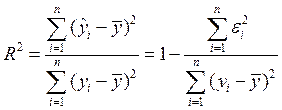, (2.5)

где 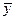- среднее значение зависимой переменной,

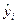- предсказанное (расчетное) значение зависимой переменной.

Коэффициент детерминациипоказывает долю вариации результативного признака, находя­щегося под воздействием изучаемых факторов, т. е. определяет, ка­кая доля вариации признака Y учтена в модели и обусловлена влия­нием на него факторов.

Чем ближе 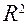к 1, тем выше качество модели.

Для оценки качества регрессионных моделей целесообразно также ис­пользовать коэффициент множественной корреляции (индекс корреляции) R

R = 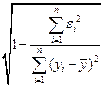= 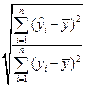(2.6)

Данный коэффициент является универсальным, так как он отра­жает тесноту связи и точность модели, а также может использовать­ся при любой форме связи переменных.

Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров.

Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y

Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет.

Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с n₁= k и n₂ = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

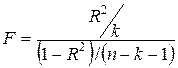(2.7)

В качестве меры точности применяют несмещенную оценку дис­персии остаточной компоненты, которая представляет собой отно­шение суммы квадратов уровней остаточной компоненты к величи­не (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины ( 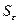) называется стандартной ошибкой:

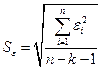(2.8)

значимость отдельных коэффициентов регрессии проверяется по t-статистике пу­тем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

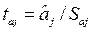, (2.9)

где S_aj— это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии a_j.Величина S_aj представляет собой квадратный корень из произ­ведения несмещенной оценки дисперсии 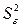и j -го диагонального эле­мента матрицы, обратной матрице системы нормальных уравнений.

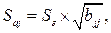
где 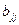- диагональный элемент матрицы .

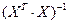Если расчетное значение t-критерия с (n - k - 1) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели (при этом ее качество не ухудшится).

Проверка выполнения предпосылок МНК.

Рассмотрим выполнение предпосылки гомоскедастичности, или равноизменчивости случайной составляющей (возмущения).

Невыполнение этой предпосылки, т.е. нарушение условия гомоскедастичности возмущений означает, что дисперсия возмущения зависит от значений факторов. Такие регрессионные модели называются моделями с гетероскедастичностью возмущений.

Обнаружение гетероскедастичности

Для обнаружения гетероскедастич­ности обычно используют тесты, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда - Квандта, тест Глейзера, двусторонний критерий Фишера и другие [2].

При малом объеме выборки для оценки гетероскедастич­ности может использоваться метод Голдфельда — Квандта.

Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков воз­растает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая 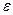распределена нормально.

Чтобы оценить на­рушение гомоскедастичности по тесту Голдфельда - Квандта необходимо выполнить следующие шаги.