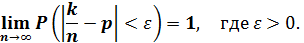Ковариация и коэффициент корреляции

Пусть имеется двумерная случайная величина (Х и Y).

Степень зависимости её составляющих Х и Y, выражает ковариация и коэффициент корреляции.

Ковариацией или корреляционным моментом называется математическое ожидание произведения отклонений случайных величин Х и Y от их математических ожиданий.

Обозначается:

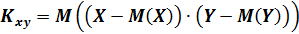
Раскрыв скобки и преобразовав формулу, мы получим:

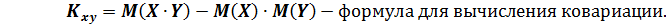
Коэффициентом корреляции называется отношение ковариации случайных величин Х и Y к произведению их средних квадратических отклонений:

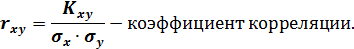
Свойства коэффициента корреляции:

1) Коэффициент корреляции принимает значение на отрезке 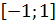, то есть

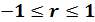
2) Если случайные величины Х и Y независимы, то их коэффициент корреляции равен нулю, то есть .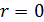

Если 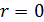, то случайные величины называются некоррелированными.

3) Если коэффициент корреляции двух случайных величин равен по модулю единице, то есть 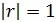, то между этими случайными величинами существует линейная функциональная зависимость.

Пример 1. Закон распределения дискретной двумерной случайной величины (X, Y) задан в таблице:

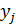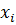	‒1
	0,10	0,25	0,30	0,15
	0,10	0,05	0,00	0,05

Найти:

а) законы распределения одномерных случайных величин X и Y;

б) условные законы распределения случайной величины X при условии Y = 2 и случайной величины Y при условии X = 1;

в) вычислить P(Y<X);

г) ковариацию и коэффициент корреляции случайных величин X и Y.

Решение:

а) Случайная величина X может принимать значения:

X = 1 с вероятностью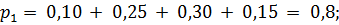

X = 2 с вероятностью 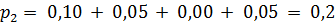, т.е. ее закон распределения:

X:

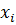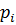	0,8	0,2

Аналогично закон распределения Y:

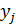	‒1
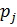	0,2	0,3	0,3	0,2

б) Условный закон распределения X при условии, что Y = 2, получим, если вероятности 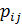, стоящие в последнем столбце первоначальной таблицы, разделим на их сумму, т.е. на 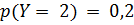. Получим:

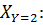
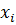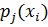	0,75	0,25

Аналогично для получения условного закона распределения Y при условии X = 1 вероятности 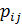, стоящие в первой строке первоначальной таблицы, делим на их сумму, т.е. на 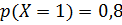. Получим:

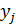	‒1
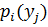	0,125	0,3125	0,375	0,1875

в) Для нахождения вероятностей P(Y<X) складываем вероятности событий 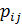из первоначальной таблицы, для которых
.

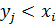Получим:

P(Y<X) = 0,10 + 0,25 + 0,10 + 0,05 + 0,00 = 0,5.

г) Найдем математические ожидания и средние квадратические отклонения этих случайных величин:

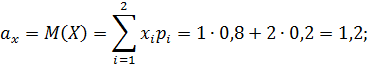
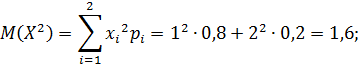
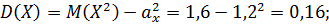
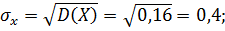
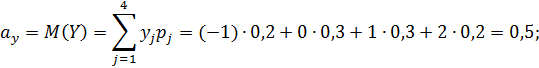
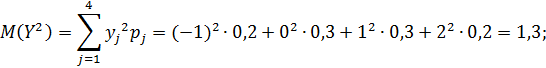
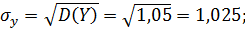
Так как

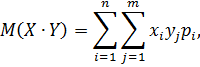
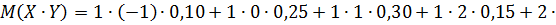
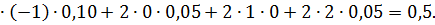
Вычислим ковариацию 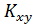по формуле:

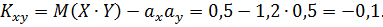
Вычислим коэффициент корреляции 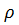по формуле:

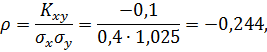
т.е. между случайными величинами X и Y существует отрицательная линейная зависимость; следовательно, при увеличении (уменьшении) одной из случайных величин другая имеет некоторую тенденцию уменьшаться (увеличиваться).

Закон больших чисел.

С вероятностью сколь угодно близкой к единице можно утверждать, что частота наступления события при большом числе опытов 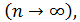сколь угодно мало отличается от вероятности наступления этого события в отдельном опыте.