Теорема о сумме произведений на алгебраическое выражение

определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т.е.

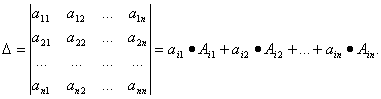Теорема о сумме произведений на алгебраическое выражение - student2.ru (i = 1, 2, ..., n)

Метод Крамера

Рассмотрим систему n линейных уравнений с n неизвестных х1, х2,…хn В этой системе число уравнений равно числу неизвестных.

a11x1+a12x2+…+a1nxn=b1

a21x1+a22x2+…+a2nxn=b2 (1)

………………………….

an1x1+an2x2+…+annxn=bn

Матрица системы (1) имеет n строк и n столбцов т.е. является квадратной матрицей n-ого порядка. Определитель:

a11a12…a1n

D= a21a22…a2n

………….

an1an2…ann

этой матрицы является определителем системы.j-ый столбец системы т.е. столбец из коэффициентов при неизвестных xj, обозначим Aj;столбец, составленный из свободных коэффициентов системы через В. Тогда Dj(B) представляет собой определитель, полученный из определителя D заменой столбца Aj столбцом B.

a11a12…b1…a1n

Dj(В)= a21a22…b2…a2n

……………….

an1an2…bn…ann

Т.о. сформулируем теорему Крамера: Если главный определитель системы n линейных уравнений отличен от 0 , то система совместна и имеет единственное решение. Это решение даётся следующим образом, значениями неизвестных:

xj=Dj(В)/D (j=1,2,…,n) (2)

Доказательство: Докажем сначала, что если D<>0 , то система (1) совместна и имеет единственное решение.

Для этого выпишем расширенную матрицу системы (1):

a11a12…a1n b1

a21a22…a2n b1

…………… …

an1an2…ann bn

Каждый из столбцов этой матрицы можно считать некоторым вектором n-мерного пространства. Введём для них обозначения:

a11 a11 a1n b1

I1= a21 , I2= a22 , In= a2n , b= b2

… a.. … …

an1 an2 ann bn

Определитель D , составленный из коэффициентов векторов (I1, I2,… In) по условию отличен от 0. Значит эти векторы образуют базис линейного пространства.

Если использовать векторное обозначение , то систему (1) можно записать:

X1I1+x2I2+…+xnIn=b

Отсюда видно, что неизвестные x1, x2,…xn - не что иное как координаты вектора b в базисе. Но ведь любой вектор можно, и при том единственным способом, разложить по любому заданному базису. Поэтому система (1) имеет единственное решение.

Докажем, что решение системы (1) находится по формулам (2) D<>0

Предположим, что Х1, Х2 , … ,Хn – решение системы (1) умножим j-ый столбец определителя D на Xj. Тогда и сам определитель D умножим на Xj. Получим новый определитель:

а11 а12 … хjа1j … а1n

a12 а22 … хjа2j … а2n

Dxj = ……………………..

аn1 аn2 … xjanj … аnn

Прибавим к j-му столбцу этого определителя линейную комбинацию его остальных столбцов, которую составляем по следующему правилу: первый столбец умножаем на х1 , второй – на х2, и т. д., последний столбец – на хn .

В результате такого преобразования определитель не изменится, не изменятся и все его столбцы, кроме j – го , а в j–ом появятся новые элементы .

Например в 1 – ой строке j – го столбца появится сумма: а11х1+а12х2+…+а1jхj+…+а1nхn

равная левой части 1 – ого уравнения (1). Но т.к. по предположению х1 , х 2 , … , хn – решение системы (1), то эта система равна b1 . Значит в 1 – ой строке j – го столбца, появится элемент b1 , во второй – b2 , в последней (n – ой) – bn

Dxj примет вид определителя:

а11 а12 … b1 … a1n

Теорема о сумме произведений на алгебраическое выражение - student2.ru a21 a22 … b2 … а2n = Dj(b)