Розв’язання однорідних систем лінійних алгебраїчних рівнянь.
ЛЕКЦІЯ № 4
Тема № 4. Дослідження довільних систем лінійних алгебраїчних рівнянь (СЛАР) та їх розв’язання методом Гаусса.
з навчальної дисципліниЛінійна алгебра та аналітична геометрія
напряму підготовки УПРАВЛІННЯ ІНФОРМАЦІЙНОЮ БЕЗПЕКОЮ
освітньо-кваліфікаційного рівня БАКАЛАВР
Лекція розроблена
Кандидатом фізико-математичних наук Жихарєвою Ю.І.
Навчальна та виховна мета:
1. Студенти повинні знати теоретичні питання з теми «Системи лінійних алгебраїчних рівнянь»: означення СЛАР, види СЛАР; алгоритм дослідження СЛАР.
2. Студенти повинні вміти досліджувати СЛАР на сумісність та визначеність. 3.Розвиток мислення студентів, залучення до вивчення математики, як необхідної складової фахівця технічного університету
План.
1. Розв’язання однорідних систем лінійних алгебраїчних рівнянь.
2. Дослідження систем лінійних алгебраїчних рівнянь на сумісність. Теорема Кронекера-Капеллі
ЛІТЕРАТУРА:
1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.: ЦУЛ, 2002 – 401 с.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – Москва: Наука, – 1988 – 240 с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч 1-2. Москва.: Высшая школа, 1986.
4. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум. - К.:ЦУЛ, 2003 – 536 с.
5. Овчинніков П.Ф., Яремчик Ф.П., Михайленко В.М. Вища математика. – К.: Техніка, ч.І 596 с., ч.ІІ 792 с., 2000.
Конспект лекції
Розв’язання однорідних систем лінійних алгебраїчних рівнянь.
Визначення. Система лінійних алгебраїчних рівнянь, в якій всі вільні члени дорівнюють 0 називається однорідною системою лінійних алгебраїчних рівнянь (ОСЛАР).
Загальний вигляд однорідної системи лінійних алгебраїчних рівнянь такий:
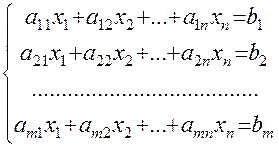(3)
Однорідна система лінійних алгебраїчних рівнянь завжди сумісна, тому що для всіх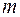 
, 
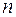і коефіцієнтів 
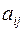вона має розв’язок 0, 0,..., 0.Цей розв’язок називається нульовим або тривіальним. Будь-який розв’язок однорідної СЛАР, відмінний від нульового, називається ненульовим або нетривіальним.
Теорема (необхідна і достатня ознака сумісності ОСЛАР (3) ). Для того, щоб однорідна система лінійних алгебраїчних рівнянь (3) була сумісною, тобто мала нетривіальні розв’язки, необхідно і достатньо, щоб ранг матриці системи був менший числа невідомих.
ОСЛАР (3) сумісна (має ненульові розв’язки)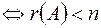 
Наслідок. Однорідна система лінійних алгебраїчних рівнянь, в якій число рівнянь дорівнює числу невідомих має ненульові розв’язки тоді і тільки тоді, коли її визначник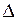 
дорівнює нулю.
Дійсно, рівність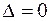 
означає, означає, що ранг матриці системи менше .
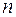Розв’язки однорідної системи лінійних алгебраїчних рівнянь мають наступні властивості.
1) Якщо набір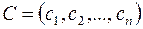 
є розв’язком системи (3), то для будь-якого числа 
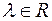набір 
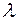
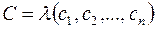
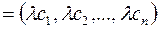також буде розв’язком системи (3).
2) Якщо набори 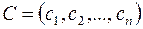і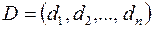 
є розв’язками системи (3), то набір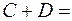 
+ 
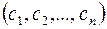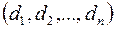також буде розв’язком системи (3).
3) Якщо набори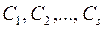 
є розв’язками системи (3), то набір 
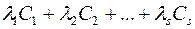, де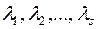 
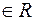також буде розв’язком системи (3).
Нехай однорідна система (3) невизначена, тобто має безліч розв’язків. Кожен її розв’язок – це деякий набір 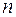чисел, всі розв’язки утворюють нескінченну множину наборів 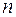чисел.
Теорема. (про структуру розв’язків ОСЛАР). Всі розв’язки однорідної система лінійних алгебраїчних рівнянь можна записати у вигляді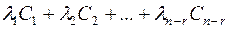 
, де 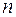- число невідомих, 
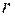- ранг матриці системи,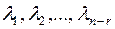 
.
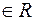Набір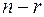 
розв’язків 
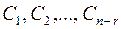, про який йдеться в останній теоремі називається базисною системою розв’язків.
Запис
= ,
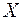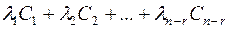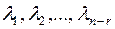
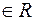
називається загальним розв’язком ОСЛАР. Таким чином, загальний розв’язок ОСЛАР являє собою матрицю-рядок .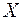
З теорем випливає наступна