Плоскость в пространстве. Прямая в пространстве. Прямая и плоскость в пространстве

(Доцент: Зубков А.Н., ТФ ДГТУ)

1. Аналогично линиям на плоскости поверхности (S) в пространстве Е³ задаются уравнениями вида

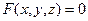(1)

в прямоугольной д.с.к. Oxyz. Уравнению (1) удовлетворяют координаты каждой точки 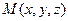, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Например, пусть дана сфера:

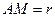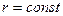, > 0, (2)

т.е. множество точек 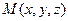, находящихся от точки 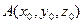на постоянном расстоянии. Применяя формулу расстояния между двумя точками А и М, получим из (2) уравнение вида

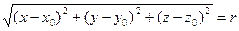
или

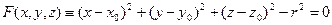. (3)

Это и есть искомое уравнение для сферы.

Таким образом, поверхность (S) в Е³ можно задать геометрически и аналитически. Если (S) дана аналитически с помощью уравнения (1), то возникает задача об исследовании формы этой поверхности.

Линию (L) в Е³ можно рассматривать как линию пересечения двух поверхносте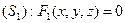й и 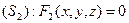. Поэтому координаты точек 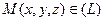удовлетворяют системе двух уравнений с тремя неизвестными:

1. 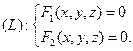(4)

Например, 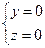- уравнение оси Oz.

-2-

Линию (L) в Е³ можно рассматривать как траекторию движения точки. В этом случае ее задают векторным уравнением

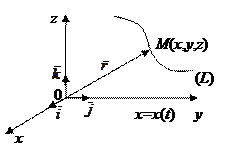
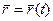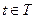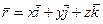, , где . (5)

Из (5) получаем параметрические уравнения линии (L):

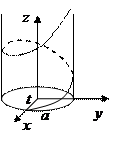
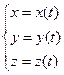. Например, 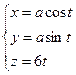- уравнение винтовой линии.

Здесь 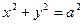, т.е. эта линия лежит на цилиндре и ® 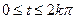, 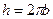- шаг винта.

П. 2. Уравнения плоскости П в Е³

Простейшей поверхностью в Е³ является плоскость П.

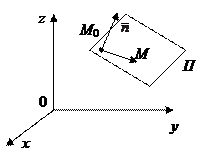а) Положение П в Е³ можно задать, если указать точку 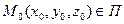и вектор 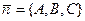, 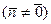- нормальный к П, т.е. 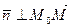, 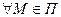. Это означает, что

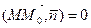. (6)

Уравнение (6) называется уравнением плоскости П в векторной форме. Применяя формулу скалярного произведения двух векторов и

-3-

учитывая, что 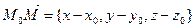, получим из (6) уравнение для П в координатной форме, проходящей через данную точку перпендикулярно вектору :

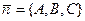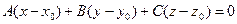, (7)

где 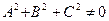, так как .

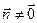Уравнение (7) определяет в общем не одну плоскость П, а связку плоскостей, проходящих через точку М₀ для переменных А, В и С - координат вектора .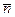

б) Преобразуем уравнение (7) к виду:

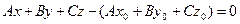
или

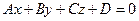. (8)

Уравнение (8) называется общим уравнением плоскости П в Е³. Если 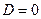, то П проходит через начало 0 координат Oxyz.

в) Пусть 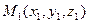, , 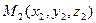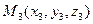- три различные точки в Е³, не лежащие на одной прямой. Тогда через них проходит единственная плоскость П. Возьмем на П произвольную точку 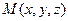и рассмотрим векторы ,

,

,

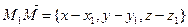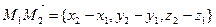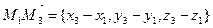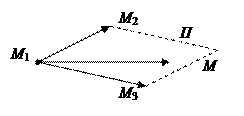с общим началом в точке М₁.

Эти векторы лежат на плоскости П, т.е. компланарны, и потому их смешанное произведение равно нулю

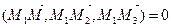. (9)

-4-

Из 9 получаем уравнение плоскости П, проходящей через три данные точки в координатной форме:

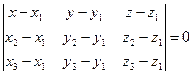. (10)

г) Пусть П пересекает оси Ox, Oy, Oz в точках 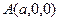, 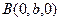и 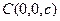соответственно. Подставляя координаты этих точек в (10), получим

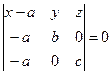
или 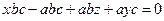,т.е.

.

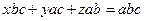Следовательно, получаем уравнение

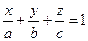(11)

Уравнение (11) называется уравнением плоскости П в Е³ в отрезках на осях.

д) Пусть 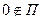. Обозначим через р расстояние от точки 0 до П:

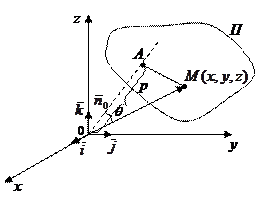
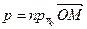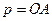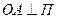, где , , а 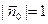, т.е. .

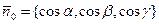Так как (выше) 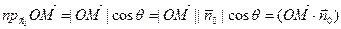, (12) то из (12) получаем уравнение для П:

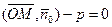. (13)

Учитывая, что 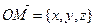, , 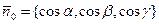запишем (13) в силу в виде

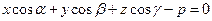, р > 0.(14)

Это уравнение называют нормальным уравнением плоскости в координатной форме.

-5-

Общее уравнение (8) для П можно привести к виду (14), если умножить его на нормирующий множитель m, определяемый условиями:

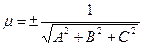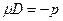1) ; 2) < 0.

Так как 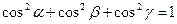, то 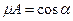, , 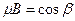, 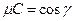как это видно из (14).

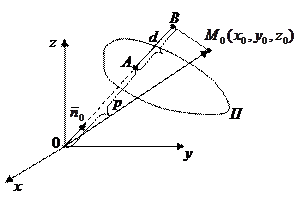Задача 1. Найти расстояние d от точки 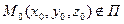, до П. Имеем 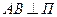, 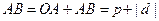. Тогда

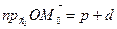или

.

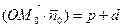Отсюда находим

.

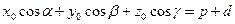Следовательно,

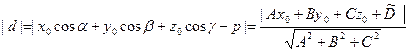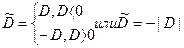, .(15)

Задача 2. Найти угол j между двумя плоскостями

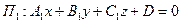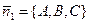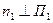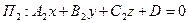, где , ,

, где , .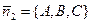

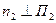Так как 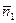и 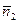однозначно определяют положение П₁ и П₂ в Е³, то под углом j между двумя плоскостями П₁ и П₂ понимается угол между векторам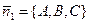и и 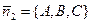, нормальными к этим плоскостям. Тогда по формуле угла между двумя векторами имеем .

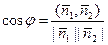Или

-6-

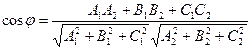. (16)

Из (16) следует, что

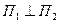Û 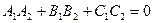., (17)

- условие перпендикулярности двух плоскостей, а если 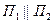, то 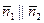и поэтому

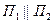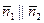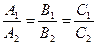Û , (18)

- условие параллельности двух плоскостей.

П. 3. Прямая в пространстве

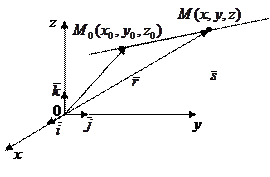а). Положение прямой L в Е³ можно определить, если задать точку 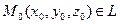и направляющий вектор , .

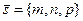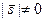Возьмем произвольную точку 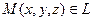и рассмотрим вектор

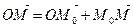, (19)

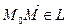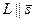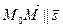. Так как , то и потому 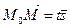, 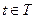. Отсюда и из (19) получаем

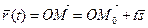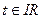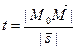, , (20)

- векторное уравнение прямой L.

б) Так как 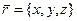, а 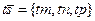, то (20) можно записать в виде

.

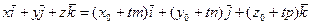Отсюда следуют равенства

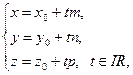(21)

которые называют параметрическими уравнениями прямой L в Е³.

в). Из (21) следуют равенства

-7-

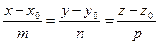. (22)

Уравнения (22) называют каноническими уравнениями прямой L в Е³. Они непосредственно следуют из условия, что .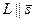

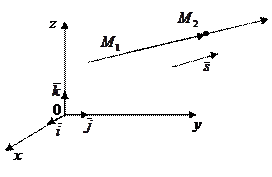M

г). Пусть даны две точк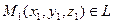и и 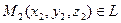. Тогда вектор 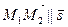. Отсюда, так как 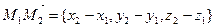, а 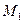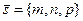, получаем уравнения

,

,

,

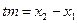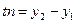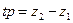из которых в силу (2.89) будем иметь

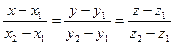. (23)

Уравнения (23) называются уравнениями прямой L в Е³, проходящей через две данных точки.

д). Прямую L в Е³ можно задать как линию пересечения двух плоскостей П₁ и П₂. Тогда система уравнений:

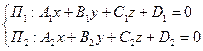(24)

и определяет прямую L.

Уравнения (24) называются общими уравнениями прямой L в Е³.

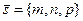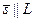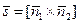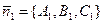е). От общих уравнений (24) прямой L в Е³ можно перейти к каноническим уравнениям (22), взяв в качестве направляющего вектора прямой L, , вектор , где и 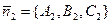- нормальные векторы для П₁ и П₂, соответственно. Принимая во внимание формулу для векторного произведения векторов, находим

-8-

.

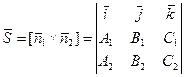Точку 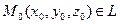найдем, решив систему (24), полагая .

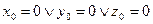Основные задачи на прямую L в Е³:

Задача 1. Найти угол j между двумя прямыми L₁ и L₂ в Е³.

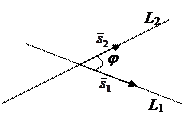Пусть

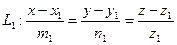
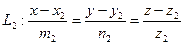(25)

Под углом j между L₁ и L₂ понимают угол 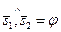. Тогда по формуле для косинуса угла между векторами получим 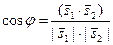. Отсюда, так как 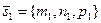, 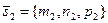в силу (25) будем иметь

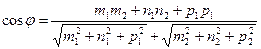. (26)

Из (26) следует, что

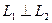Û 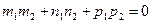. (27)

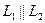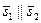Если , то и потому

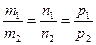(28)

- условие параллельности двух прямых в Е³.

Задача 2. Найти условие, при котором L₁ и L₂ в Е³ лежат в одной плоскости П.

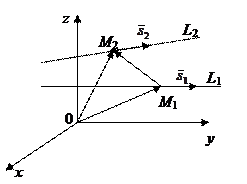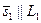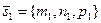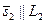Пусть , где , , где , , .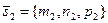

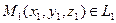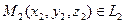-9-

Тогда 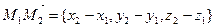. Прямые L₁ и L₂ лежат в П Û, если векторы 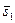, 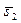и 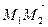- компланарны. Условием компланарности этих векторов является обращение в нуль их смешанного произведения

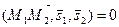, т.е.

.

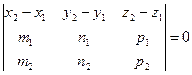Задача 3. Найти угол j между прямой L и плоскостью П в Е³.

Пусть 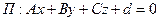, а ,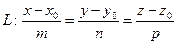

где 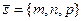, 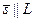. Углом между L и П называют угол меду L и ее проекцией L_П на П. 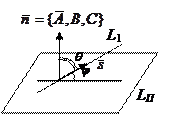Обозначим 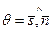. Тогда 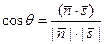, при этом 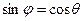, есл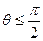и , и 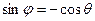, если p > q > 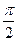. Таким образом, имеем

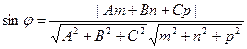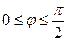, . (29)

Из (29) следует, что 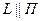Û 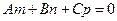, (30)

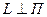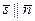а если , то , и потому получим равенства 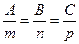, (31)

которое называют условиями перпендикулярности прямой и плоскости.

Задача 4. Найти точку 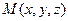пересечения прямой L и плоскости.

Пусть ,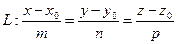

-10-

.

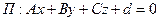Чтобы найти точку 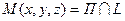, нужно решить эту систему уравнений. Проще всего это сделать, записав канонические уравнения прямой L в параметрической форме

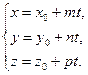(32)

Подставляя эти выражения для x, y и z в общее уравнение плоскости П, получим

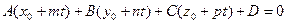или

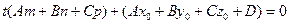. (33)

Если L ∦ П, то в силу (30) имеем 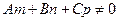,и потому из (33) получаем .

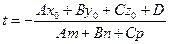Подставляя это значение t в (32), найдем координаты точки .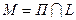

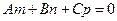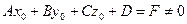Если , а , то 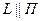и не существует точки 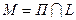, так как уравнение (33) примет вид 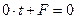, где .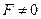

Если 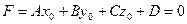, то уравнение (33) запишется в виде

.

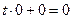Оно удовлетворяется при любом значении t, т.е. любая точка на L является точкой пересечения L с П. А это возможно, когда 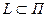. Таким образом, уравнения

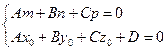(34)

дают условия принадлежности L плоскости П.