Неопределенный интеграл. Подробные примеры решений

Начнем изучение темы «Неопределенный интеграл», а также подробно разберем примеры решений простейших (и не совсем) интегралов. Как обычно, мы ограничимся минимумом теории, которая есть в многочисленных учебниках, наша задача – научиться решать интегралы.

Что нужно знать для успешного освоения материала? Для того, чтобы справиться с интегральным исчислением, Вам необходимо уметь находить производные, минимум, на среднем уровне. Не лишним опытом будет, если у Вас за плечами несколько десятков, а лучше – сотня самостоятельно найденных производных. По крайне мере, Вас не должны ставить в тупик задания на дифференцирование простейших и наиболее распространенных функций.

Казалось бы, причем здесь вообще производные, если речь в статье пойдет об интегралах?! А дело вот в чем. Дело в том, что нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия, как, например, сложение/вычитание или умножение/деление. Таким образом, без навыка и какого-никакого опыта нахождения производных, к сожалению, дальше не продвинуться.

В этой связи нам потребуются следующие методические материалы: Таблица производных и Таблица интегралов.

В чем сложность изучения неопределенных интегралов? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно четкий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приемов интегрирования. И, если способ интегрирования изначально подобран неверно (т.е. Вы не знаете, как решать), то интеграл можно «колоть» буквально сутками, как самый настоящий ребус, пытаясь приметить различные приемы и ухищрения. Некоторым даже нравится.

Между прочим, нам довольно часто приходилось слышать от студентов (не гуманитарных специальностей) мнение вроде: «У меня никогда не было интереса решить предел или производную, но вот интегралы – совсем другое дело, это увлекательно, всегда есть желание «взломать» сложный интеграл». Стоп. Хватит чёрного юмора, переходим к этим самым неопределенным интегралам.

Коль скоро способов решения существует много, то с чего же начать изучение неопределенных интегралов чайнику? В интегральном исчислении существуют, на наш взгляд, три столпа или своеобразная «ось», вокруг которой вращается всё остальное. В первую очередь следует хорошо разобраться в простейших интегралах (эта статья).

Потом нужно детально проработать урок Метод замены в неопределенном интеграле. ЭТО ВАЖНЕЙШИЙ ПРИЁМ! Может быть, даже самая важная статья из всех статей, посвященных интегралам. И, в-третьих, обязательно следует ознакомиться с методом интегрирования по частям, поскольку с помощью него интегрируется обширный класс функций. Если Вы освоите хотя бы эти три урока, то уже «не два». Вам могут «простить» незнание интегралов от тригонометрических функций, интегралов от дробей, интегралов от дробно-рациональных функций, интегралов от иррациональных функций (корней), но вот если «сесть в лужу» на методе замены или методе интегрирования по частям – то это будет очень и очень скверно.

Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:

Сразу разбираемся в обозначениях и терминах:

– значок интеграла.

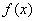– подынтегральная функция (пишется с буквой «ы»).

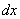– значок дифференциала. Что это такое, мы рассмотрим совсем скоро. Главное, что при записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

– подынтегральное выражение или «начинка» интеграла.

– первообразнаяфункция.

– множество первообразных функций. Не нужно сильно загружаться терминами, здесь самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа .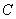

Решить неопределенный интеграл – это значит найти множество первообразных функций от данной подынтегральной функции 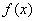, пользуясь некоторыми правилами, приемами и таблицей.

Еще раз посмотрим на запись:

Посмотрим в таблицу интегралов.

Что происходит? Левые части у нас превращаютсяв другие функции: .

Упростим наше определение:

Решить неопределенный интеграл – это значит ПРЕВРАТИТЬ его в неопределенную (с точностью до константы) функцию , пользуясь некоторыми правилами, приемами и таблицей.

Возьмем, например, табличный интеграл 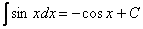. Что произошло? Символическая запись превратилась в множество первообразных функций .

Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл, или первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае 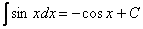совсем не обязательно понимать, почему интеграл превращается именно в . Можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.

Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найденаправильно, справедливо следующее:

Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.

Вернемся к тому же табличному интегралу .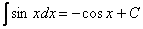

Убедимся в справедливости данной формулы. Берем производную от правой части:

– это исходная подынтегральная функция.

Вот, кстати, стало понятнее, почему к функции всегда приписывается константа 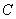. При дифференцировании константа всегда превращается в ноль.

Решить неопределенный интеграл– это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере , , , и т. д. – все эти функции являются решением интеграла . Решений бесконечно много, поэтому записывают коротко:

Таким образом, любой неопределенный интеграл достаточно легко проверить. Это некоторая компенсация за большое количество интегралов разных видов.

Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной, с двух правил интегрирования:

– константу C можно (и нужно) вынести за знак интеграла.

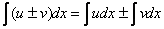– интеграл суммы (разности) двух функций равен сумме (разности) двух интегралов. Данное правило справедливо для любого количества слагаемых.

Как видите, правила, в принципе, такие же, как и для производных. Иногда их называют свойствами линейности интеграла.

Пример 1

Найти неопределенный интеграл.

.

Выполнить проверку.

Решение: Удобнее преобразовать его, как.

(1) Применяем правило 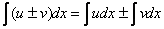. На забываем записать значок дифференциала dx под каждым интегралом. Почему под каждым? dx– это полноценный множитель. Если расписывать детально, то первый шаг следует записать так:

.

(2) Согласно правилу выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом tg5 – это константа, её также выносим.

Кроме того, на данном шаге готовим корни и степени для интегрирования. Точно так же, как и при дифференцировании, корни надо представить в виде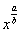 . Корни и степени, которые располагаются в знаменателе – перенести вверх.

Примечание: в отличие от производных, корни в интегралах далеко не всегда следует приводить к виду 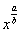, а степени переносить вверх.

Например, – это готовый табличный интеграл, который уже посчитали до Вас, и всякие китайские хитрости вроде совершенно не нужны. Аналогично: – это тоже табличный интеграл, нет никакого смысла представлять дробь в виде . Внимательно изучите таблицу!

(3) Все интегралы у нас табличные. Осуществляем превращение с помощью таблицы, используя формулы: , и

для степенной функции - .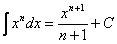

Следует отметить, что табличный интеграл – это частный случай формулы для степенной функции: .

Константу C достаточно приплюсовать один раз в конце выражения

(а не ставить их после каждого интеграла).

(4)Записываем полученный результат в более компактном виде, когда все степени вида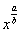

снова представляем в виде корней, а степени с отрицательным показателем сбрасываем обратно в знаменатель.

Проверка. Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:

Получена исходная подынтегральная функция, т. е. интеграл найден правильно. От чего плясали, к тому и вернулись. Хорошо, когда история с интегралом заканчивается именно так.

Время от времени встречается немного другой подход к проверке неопределенного интеграла, когда от ответа берется не производная, а дифференциал:

.

В итоге получаем не подынтегральную функцию, а подынтегральное выражение.

Не стоит пугаться понятия дифференциал.

Дифференциал – это производная, умноженная на dx.

Однако нам важны не теоретические тонкости, а то, что с этим дифференциалом дальше делать. Дифференциал раскрывается следующим образом: значок d убираем, справа над скобкой ставим штрих, в конце выражения приписываем множитель dx:

Получено исходное подынтегральное выражение, то есть интеграл найден правильно.

Как видите, дифференциал сводится к нахождению производной. Второй способ проверки мне нравится меньше, так как приходиться дополнительно рисовать большие скобки и тащить значок дифференциала dx до конца проверки. Хотя он корректнее, или «солиднее», что ли.

На самом деле можно было умолчать о втором способе проверки. Дело не в способе, а в том, что мы научились раскрывать дифференциал. Еще раз.

Дифференциал раскрывается следующим образом:

1) значок d убираем;

2) справа над скобкой ставим штрих (обозначение производной);

3) в конце выражения приписываем множитель dx.

Например:

.

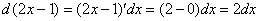Запомните это. Рассмотренный приём потребуется нам очень скоро.

Пример 2

Найти неопределенный интеграл. Выполнить проверку.

.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Когда мы находим неопределенный интеграл, то ВСЕГДА стараемся сделать проверку, тем более, для этого есть прекрасная возможность. Далеко не все типы задач в высшей математике являются подарком с этой точки зрения. Неважно, что часто в контрольных заданиях проверки не требуется, её никто, и ничто не мешает провести на черновике. Исключение можно сделать лишь тогда, когда не хватает времени (например, на зачете, экзамене). Лично я всегда проверяю интегралы, а отсутствие проверки считаю халтурой и некачественно выполненным заданием.

Пример 3

Найти неопределенный интеграл:

. Выполнить проверку.

Решение: Анализируя интеграл, мы видим, что у нас под интегралом произведение двух функций, да еще и возведение в степень целого выражения. К сожалению, на поприще интегральной битвы нет хороших и удобных формул для интегрирования произведения и частного в виде: или .

Поэтому, когда дано произведение или частное, всегда имеет смысл посмотреть, а нельзя ли преобразовать подынтегральную функцию в сумму? Рассматриваемый пример – тот случай, когда можно.

Сначала приведём полное решение, комментарии будут ниже.

(1) Используем старую добрую формулу квадрата суммы для любых действительных чисел 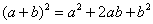, избавляясь от степени над общей скобкой.

(2) Вносим 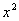в скобку, избавляясь от произведения.

(3) Используем свойства линейности интеграла (оба правила сразу).

(4) Превращаем интегралы по табличной формуле .

(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь – она несократима и в ответ входит именно в таком виде.

Не нужно делить на калькуляторе !

Не нужно представлять ее в виде !

Проверка:

Получена исходная подынтегральная функция, а значит, интеграл найден правильно.

В ходе проверки функцию всегда желательно «упаковать» до первоначального вида, вынося, в данном случае, 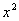за скобки и применяя формулу сокращенного умножения в обратном направлении: .

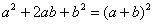Пример 4

Найти неопределенный интеграл

. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Пример 5

Найти неопределенный интеграл

. Выполнить проверку.

В данном примере подынтегральная функция представляет собой дробь. Когда мы видим в подынтегральном выражении дробь, то первой мыслью должен быть вопрос: «А нельзя ли как-нибудь от этой дроби избавиться, или хотя бы её упростить?».

Замечаем, что в знаменателе находится одинокий корень из «икс». Один в поле – не воин, значит, можно почленно разделить числитель на знаменатель:

Действия с дробными степенями мы не комментируем, так как о них неоднократно шла речь в статьях о производной функции.

Если Вас все-таки ставит в тупик такой пример, как

,

и ни в какую не получается правильный ответ ,

то рекомендуем обратиться к школьным учебникам. В высшей математике дроби и действия с ними встречаются на каждом шагу.

Также обратите внимание, что в решении пропущен один шаг, а именно, применение правил , 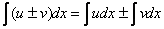. Обычно при определенном опыте решения интегралов данные правила считают очевидным фактом и не расписывают подробно.

Пример 6

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

В общем случае с дробями в интегралах не всё так просто, дополнительный материал по интегрированию дробей некоторых видов можно найти в статье: Интегрирование некоторых дробей. Но, прежде чем перейти к вышеуказанной статье, необходимо ознакомиться с уроком: Метод замены в неопределенном интеграле. Дело в том, что подведение функции под дифференциал или метод замены переменной является ключевым моментомв изучении темы, поскольку встречается не только «в чистых заданиях на метод замены», но и во многих других разновидностях интегралов.

Решения и ответы:

Пример 2: Решение:

Пример 4: Решение:

В данном примере мы использовали формулу сокращенного умножения

Пример 6: Решение: