Разложение основных элементарных функций

Теорема 2.1.Если функция f(x) определена и имеет производные сколь угодно высоких порядков и существует постоянная, такая, что при лю­бых х и п удовлетворяет неравенству 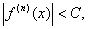то функция f(x) разлагается в ряд Тейлора (1.2) при любом x₀.

Приведем без доказательства следующие разложения элементарных функций в ряд Маклорена

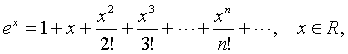
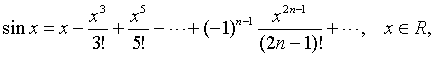
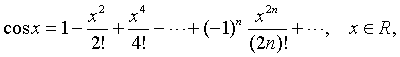
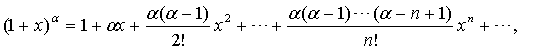
это разложение имеет место при любом натуральном значении 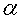и любом значении x, если число 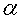не является натуральным, то данное равенство справедливо лишь при –1<x<1;

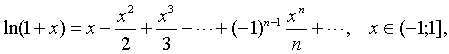
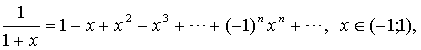
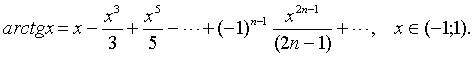
Показательная функция — математическая функция {\displaystyle f(x)=a^{x}} , где {\displaystyle a} называется основанием степени, а {\displaystyle x} — показателем степени.

В теории функций некоторое комплексное число z=x+y⋅i, где x,y∈R, рассматривают в качестве комплексной переменной. Каждое значение комплексного переменного z можно изобразить на комплексной плоскости xOy с помощью точки (x;y). Следовательно, каждому значению комплексного переменного ставится в соответствие точка комплексной плоскости.

Определение 1 Комплексная величина w называется функцией комплексного переменного z, если каждому значению комплексного переменного z соответствует определенное значение комплексной величины w. Обозначение: w=f(z). Среди функций комплексного переменного рассматривают те же функции, что и для действительных переменных, в частности, показательную функцию и т.д.

Определение 2 Функция комплексного переменного, задаваемая формулой w=ez, называется показательной функцией комплексного переменного. Каждое значение показательной функции w=ez определяется следующим образом: w=ex+yi ex+yi=ex⋅(cos⁡y+i⋅sin⁡y) Следовательно, w(z)=ex⋅(cos⁡y+i⋅sin⁡y).

Пример 1 Вычислить значение показательной функции комплексного переменного w=ez при:

1) z=2+π4⋅i; 2) z=0+π⋅i; 3) z=4+0⋅i. Решение: Значение определяем по формуле: w(z)=ex⋅(cos⁡y+i⋅sin⁡y). 1) Для z=2+π4⋅i получаем w(2+π4⋅i)=e2+π4⋅i=e2⋅(cos⁡π4+i⋅sin⁡π4)=e2⋅(22+i⋅22).

2) Для z=0+π⋅i получаем w(0+π⋅i)=e0+π⋅i=e0⋅(cos⁡π+i⋅sin⁡π)=e0⋅(−1+i⋅0)=−1+0⋅i.

3) Для z=4+0⋅i получаем w(4+0⋅i)=e4+0⋅i=e4⋅(cos⁡0+i⋅sin⁡0)=e4⋅(1+i⋅0)=e4.

Свойства показательной функции комплексного переменного w=ez аналогичны свойствам показательной функции действительного переменного y=ex. Свойства: 1) ez1+z2=ez1⋅ez2 (z1=x1+y1⋅i,z2=x2+y2⋅i); 2) ez1−z2=ez1ez2 (z1=x1+y1⋅i,z2=x2+y2⋅i); 3) (ez)m=emz(m∈Z,z=x+y⋅i); 4) ez+2πi=ez(z=x+y⋅i).

Замечание Показательная функция комплексного переменного w=ez является периодической функцией, период которой равен 2π.
Формула Эйлера устанавливает взаимосвязь между экспоненциальной функцией 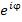и тригонометрическими функциям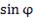и и 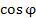на множестве комплексных чисел:

.

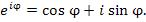(1)

Доказательство формулы Эйлера основано на представлении этих функций в виде степенных рядов и при первом чтении может быть опущено без ущерба для понимания последующего изложения.
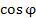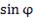Заметим, что и представляют собой соответственно вещественную и мнимую части экспоненциальной функции :

.

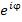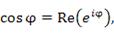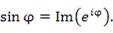(2)

Выполним в формуле Эйлера замену :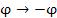

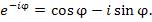(3)

Выполнив почленное сложение и вычитание выражений в обеих частях равенств (1) и (3), получим

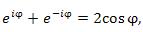
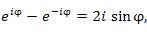
что влечет

.

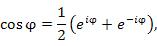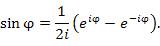(4)

Таким образом, тригонометрические функци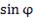и и 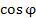представлены в виде линейных комбинаций экспоненциальных функций 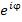и .
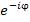Тангенс аргумента φ выражается через 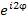: