Функции нескольких переменных

Производная. Рассмотрим некоторую функцию y = f ( x ) в двух точках x0 и x0 + 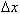 : f ( x0 ) и f ( x0 +
: f ( x0 ) и f ( x0 + 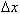 ). Здесь через
). Здесь через 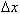 обозначенонекоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x0 +
обозначенонекоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x0 + 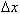 ) f ( x0) называется приращением функции. Производной функции y = f ( x ) в точке x0называется предел:
) f ( x0) называется приращением функции. Производной функции y = f ( x ) в точке x0называется предел:
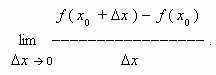
Если этот предел существует, то функция f ( x ) называется дифференцируемой в точке x0 . Производная функции f ( x ) обозначается так:
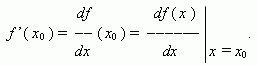
Геометрический смысл производной. Рассмотрим график функции y = f ( x ):
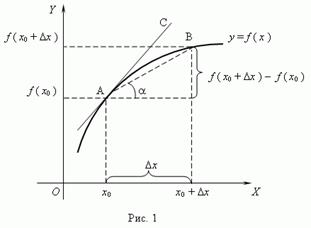
Из рис.1 видно, что для любых двух точек A и B графика функции:
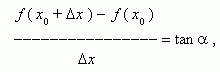
где 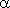 - угол наклона секущей AB.
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то 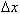 неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + 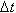 точка перемещается на расстояние: x ( t0 +
точка перемещается на расстояние: x ( t0 + 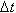 ) x ( t0 ) =
) x ( t0 ) = 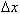 , а её средняя скорость равна:va =
, а её средняя скорость равна:va = 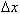
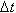 . При
. При 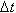
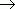 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:
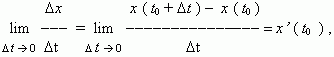
отсюда, v ( t0) = x’ ( t0) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смыслпроизводной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).
Правила дифф функций
- Постоянный множитель c можно выносить за знак производной:
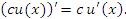
Правило 1 непосредственно вытекает из определения производной функции и свойства пределов функций, согласно которому постоянный множитель можно выносить за знак предела.
- Если существуют производные
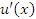 и
и 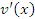 , то производная от суммы (разности) функций
, то производная от суммы (разности) функций 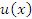 и
и 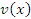 равна сумме (разности) производных:
равна сумме (разности) производных:
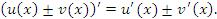
Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов. - Если существуют производные
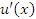 и
и 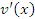 , то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
, то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
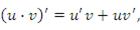
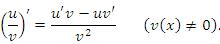
1. Первообразная и неопределенный интеграл. Интегрирование по частям и подстановкой.
Функция F(x)F(x) называется первообразной функции f(x),f(x), заданной на некотором множестве X,X, если F′(x)=f(x)F′(x)=f(x) для всх x∈X.x∈X. Если F(x−)F(x−) первообразная функции f(x),f(x), то Φ(x)Φ(x)является первообразной той же функции в том и только в том случае, когда Φ(x)=F(x)+C,Φ(x)=F(x)+C, где CC - некоторая постоянная. Совокупность всех первообразных функции f(x)f(x) называется неопределенным интегралом от этой функции и обозначается символом
∫f(x)dx.∫f(x)dx.
Таким образом, по определению
∫f(x)dx=F(x)+C,∫f(x)dx=F(x)+C,
где F(x)F(x) одна из первообразных функции f(x)f(x) а постоянная CC принимает действительные значения.
