Понятие площади плоской фигуры. Вычисление площади плоской фигуры с помощью определенного интеграла
Фигура называется простой, если ее можно разбить на конечное число треугольников. Треугольник мы понимаем как треугольную область, т. е. конечную часть плоскости, ограниченную треугольником.
На рисунке 102 изображен выпуклый многоугольник ABCDE, который является простой фигурой, так как его можно разбить на треугольники ЕАВ, ЕВС, ECD.
Площадь простой фигуры — это положительная величина, численное значение которой обладает следующими свойствами:
1. Равные фигуры имеют равные площади.
2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.
3. Площадь квадрата со стороной, равной единице измерения, равна единице.
Вычисление площадей с помощью интеграла.
1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :
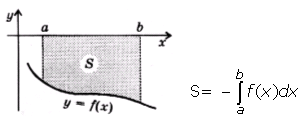
2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), 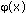 и прямыми х=а, х= b :
и прямыми х=а, х= b :
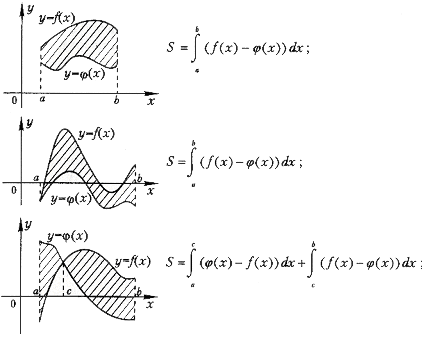
3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и 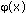 :
:
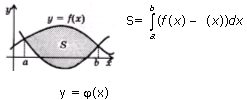
4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), 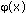 и осью Ох:
и осью Ох:
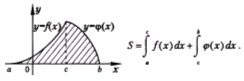
Функциональные последовательности и ряды. Равномерная сходимость. Степенные ряды в действительной и комплексной области. Радиус и круг сходимости.
Если каждому числу  из натурального ряда чисел поставлена в соответствие функция
из натурального ряда чисел поставлена в соответствие функция 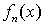 , то множество функций
, то множество функций 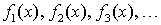 называется функциональной последовательностью
называется функциональной последовательностью  .Каждая из функций
.Каждая из функций 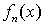 называется элементом
называется элементом  или членом функциональной последовательности
или членом функциональной последовательности  .Сумму
.Сумму 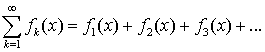 элементов функциональной последовательности
элементов функциональной последовательности 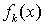 называютфункциональным рядом
называютфункциональным рядом  .Сами функции
.Сами функции 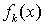 , стоящие в ряде, называют элементами
, стоящие в ряде, называют элементами  или членами ряда
или членами ряда  .Множество
.Множество 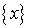 , на котором определены функции
, на котором определены функции 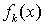 , называют областью определения функциональной последовательности
, называют областью определения функциональной последовательности  или функционального ряда
или функционального ряда  . Когда из контекста ясно, что речь идет именно о функциональной последовательности или функциональном ряде, то иногда слово «функциональный» для краткости опускают. Как и в случае числового ряда, сумму первых
. Когда из контекста ясно, что речь идет именно о функциональной последовательности или функциональном ряде, то иногда слово «функциональный» для краткости опускают. Как и в случае числового ряда, сумму первых 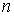 элементов
элементов 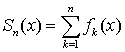 называют
называют 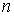 -ой частичной суммой
-ой частичной суммой  . Если взять в качестве
. Если взять в качестве 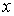 некоторую точку
некоторую точку 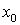 из области определения
из области определения 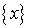 , то функциональная последовательность станет числовой
, то функциональная последовательность станет числовой  , а функциональный ряд станет числовым рядом
, а функциональный ряд станет числовым рядом  . Если в этом случае последовательность (или ряд) сходится, то говорят, что последовательность (или ряд) сходится в точке
. Если в этом случае последовательность (или ряд) сходится, то говорят, что последовательность (или ряд) сходится в точке 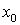 . Множество всех
. Множество всех 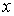 , для которых последовательность (ряд) сходится, называетсяобластью сходимости функциональной последовательности
, для которых последовательность (ряд) сходится, называетсяобластью сходимости функциональной последовательности  (функционального ряда
(функционального ряда  ).Если функциональная последовательность
).Если функциональная последовательность 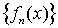 имеет область сходимости
имеет область сходимости 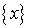 , то, вычислив в каждой точке из множества
, то, вычислив в каждой точке из множества 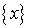 предел последовательности, получим некоторую функцию
предел последовательности, получим некоторую функцию 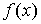 , которую называют предельной функцией последовательности
, которую называют предельной функцией последовательности 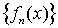
 . В том числе можно определить предельную функцию последовательности частичных сумм функционального ряда, которую называют суммой этого ряда
. В том числе можно определить предельную функцию последовательности частичных сумм функционального ряда, которую называют суммой этого ряда  .
.
Определение 1. Функциональная последовательность (31.1) называется равномерно сходящейся к функции f на множестве X, если для любого  > 0 существует такой номер n0, что для всех точек x
> 0 существует такой номер n0, что для всех точек x 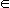 X и всех номеров n > n0 выполняется неравенство
X и всех номеров n > n0 выполняется неравенство
| fn(x) - f(x)| <  . . | (31.7) |
Очевидно, что если последовательность (31.1) равномерно сходится на множестве X к функции f, то эта последовательность сходится к функции f на рассматриваемом множестве (определение сходимости последовательности функций на множестве см. в п. 31.1).
Если последовательность { fn} сходится на множестве X к функции f, то пишут
fn 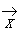 f,
f,
а если эта последовательность сходится равномерно к f на указанном множестве, то пишут
fn 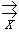 f.
f.
В символической записи определения сходящейся и равномерно сходящейся на множестве последовательности выглядят соответственно следующим образом:
fn 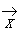 f
f 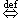
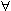
 > 0
> 0 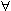 x
x 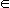 X
X 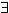 n0
n0 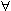 n > n0: | fn(x) - f(x)| <
n > n0: | fn(x) - f(x)| <  .
.
fn 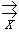 f
f 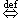
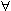
 > 0
> 0 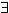 n0
n0 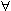 x
x 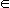 X
X  n > n0: | fn(x) - f(x)| <
n > n0: | fn(x) - f(x)| <  .
.
| Рис. 124 |
Таким образом, если последовательность { fn} только сходится к функции f на множестве X, то для каждой точки x  X существует, вообще говоря, свой номер n0 = n0(
X существует, вообще говоря, свой номер n0 = n0(  ,x), для которого при n > n0 выполняется неравенство
,x), для которого при n > n0 выполняется неравенство
| fn(x) - f(x)| <  ,
,
 и может оказаться, что для всех точек x
и может оказаться, что для всех точек x 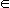 X невозможно подобрать общий номер n0, обладающий указанным свойством.
X невозможно подобрать общий номер n0, обладающий указанным свойством.
Равномерная же сходимость последовательности { fn} к функции f означает, что, какое бы число  > 0 ни задать, можно подобрать такой номер n0, что в любой точке значение функции будет отличаться от значения функции меньше, чем на (рис. 124).
> 0 ни задать, можно подобрать такой номер n0, что в любой точке значение функции будет отличаться от значения функции меньше, чем на (рис. 124).
Лемма 1. Для того чтобы последовательность { fn} равномерно сходилась на X к функции f, необходимо и достаточно, чтобы
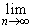 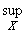 | fn(x) - f(x)| = 0. | fn(x) - f(x)| = 0. | (31.8) |
Значение этой леммы состоит в том, что она сводит понятие равномерной сходимости поледовательности { fn} функций к понятию сходимости числовой последовательности
{ 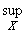 | fn(x) - f(x)|}
| fn(x) - f(x)|}
("числовой" в широком смысле этого слова: конечное число членов указанной последовательности может обратиться в +  ). В силу этого обстоятельства условие (31.8) часто бывает удобно использовать для выяснения, сходится ли равномерно интересующая нас конкретная последовательность функций.
). В силу этого обстоятельства условие (31.8) часто бывает удобно использовать для выяснения, сходится ли равномерно интересующая нас конкретная последовательность функций.
 1. Пусть
1. Пусть
fn 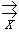 f.
f.
Зададим произвольно  > 0. Тогда существует такой номер n0, что для всех n > n0 и всех x
> 0. Тогда существует такой номер n0, что для всех n > n0 и всех x 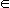 X выполняется неравенство | fn(x) - f(x)| <
X выполняется неравенство | fn(x) - f(x)| <  , а следовательно, для всех n > n0 - неравенство
, а следовательно, для всех n > n0 - неравенство
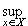 | fn(x) - f(x)| <
| fn(x) - f(x)| <  .
.
Это и означает выполнение условия (31.8).
2. Пусть выполнено условие (31.8). Зададим произвольно  > 0. Тогда в силу определения предела числовой последовательности существует такой номер n0, что для всех n > n0выполняется неравенство
> 0. Тогда в силу определения предела числовой последовательности существует такой номер n0, что для всех n > n0выполняется неравенство
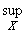 | fn(x) - f(x)| <
| fn(x) - f(x)| <  ,
,
а следовательно, для всех n > n0 и всех x 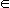 X - неравенство
X - неравенство
| fn(x) - f(x)| <  .
.
Это означает, что
fn 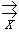 f.
f. 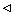
Следствие. Если существует стремящаяся к нулю последовательность { 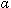 n}:
n}:
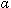 n = 0.
n = 0.
такая, что для всех x 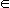 X выполняется неравенство
X выполняется неравенство
| fn(x) - f(x)| <  n, n, | (31.9) |
то последовательность { fn(x)} равномерно сходится к функции f(x) на множестве X.
 Действительно, поскольку неравенство (31.9) выполняется для всех x
Действительно, поскольку неравенство (31.9) выполняется для всех x 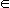 X, то
X, то
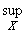 | fn(x) - f(x)| <
| fn(x) - f(x)| < 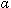 n,
n,
а поэтому из условия 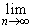
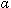 n = 0 получаем, что
n = 0 получаем, что
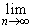
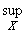 | fn(x) - f(x)| = 0.
| fn(x) - f(x)| = 0. 
Замечание 1. Очевидно, что из определения равномерной сходимости последовательности функций следует, что если какие-то последовательности равномерно сходятся на некотором множестве, то и любая их конечная линейная комбинация равномерно сходится на этом множестве.
Примеры.
1. Пусть fn(x) = xn, n = 1, 2, ..., X = [0,q], 0 < q < 1. Предел 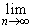 fn(x), x
fn(x), x 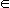 [0,q], существует и равен нулю:
[0,q], существует и равен нулю:
f(x) 
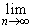 fn(x) = 0.
fn(x) = 0.
Так как 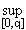 xn = qn, то
xn = qn, то
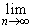
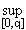 xn =
xn = 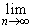 qn = 0.
qn = 0.
Следовательно, согласно лемме 1, последовательность {xn} равномерно сходится к нулю на отрезке [0,q]:
xn 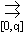 0, 0 < q < 1.
0, 0 < q < 1.
Степенные ряды –важный частный случай функциональных рядов (см. Ряд) – ряды вида
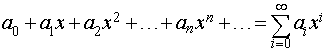 ,
,
где коэффициенты ряда а0, а1, … – некоторые постоянные.
Ряды можно рассматривать как в вещественной (действительной), так и в комплексной области.
В действительной области множество сходимости степенного ряда – внутренность интервала |x| < r, т.е. множество чисел х, таких, что –r < x < r. Граничные точки интервала сходимости могут как принадлежать, так и не принадлежать (один или оба) множеству сходимости степенного ряда.
В комплексной области множество сходимости ряда – внутренность круга радиусаr. Граничные точки этого круга могут как принадлежать, так и не принадлежать области сходимости ряда.
Область сходимости ряда может вырождаться в точку (r = 0), во всю прямую в случае действительного переменного или во всю комплексную плоскость (r = ∞).
