Вычисление определенных интегралов методом Симпсона
Для применения метода Симпсона промежуток интегрирования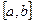 
делится равноотстоящими ординатами на четное число частей. Вместо каждых двух прямолинейных трапеций рассматривается одна трапеция, одна из сторон которой образована параболой второй степени, которая проводится через концы трех ординат, рисунок 3.
|
.Такое допущение равносильно пере-движке всей фигуры вдоль оси х. Оно не изменяет ни взаим-ного расположения 
Рис.3
ординат, ни их величины, но несколько упрощает последующие выкладки. Пусть верхняя сторона трапеции заменяется параболой, уравнение которой имеет вид:
(1).
Тогда площадь криволинейной трапеции можно выразить в виде определенного интеграла:
(2).
Поскольку парабола (I) проходит через концы ординат, то имеют место равенства
Подставляя в последние два равенства вместо 
его значение, получаем систему из двух уравнений:
(3).
Система (3) может быть решена способом Крамера. Для этого следует найти определитель системы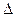 
и определители каждого неизвестного 
и 
.
Теперь легко находятся значения неизвестных:
Подставляя в (2) значения коэффициентов 
, получаем:
Окончательно имеем:
(4).
Для других трапеций, на которые разделен промежуток интегрирования можно записать аналогичные формулы:
Зоя площадь криволинейной трапеции ABCD (см. рис.1) может быть подсчитана по формуле:
Из этой формулы видно, что концевые ординаты входят в нее с коэффициентом 1, нечетные - с коэффициентом 4, а четные – коэффициентом 2. Поскольку количество трапеций, на которые разбивается промежуток интегрирования, должно быть четным, то можно полагать, что n=2m. С учетом этих замечаний формулу Симпсона можно записать в более простом виде:
Введя обозначения
получаем окончательную формулу Симпсона:
При одинаковом количестве ординат формула Симпсона дает большую точность чем формула трапеций.
Примечание:Порядок выполнения работ на ЭВМ
1. Из таблицы 1 выбрать вариант, соответствующий № фамилии студента в списке журнала посещаемости группы.
2. Составить подпрограммы-функции вычисления F(Х), и вставлять в предлагаемые модули программ.
3. Виполнить отладку программы в классе на ПК, произвести вычисления и записать результаты просчетов.
4.Оформить отчеты о проделанной работе, с записью выводов о применимости методов и их эффективности.
5. Защитить работу - студент должен ответить на вопросы преподавателя по данной работе и тождественным примерам, пояснить алгоритмы программ и результаты.
Первым листом отчета по лабораторной работе должен быть титульный лист для текстовых конструкторских документов с большим штампом , а остальные - с малым.
Все подпрограммы, вызываемые главной программой, должны быть записаны в одном файле с главной программа. ( Для всех программ данной методички )
П Р И Л О Ж Е Н И Я