Вычисление определенного интеграла (метод трапеций)
ПРИЛОЖЕНИЕ 7
FUNCTION F(X)
* Подинтегральная функция
F=COS(X**2)
RETURN
END
PROGRAM U6
PRINT*,'ЧИСЛЕННОЕ ИНТЕГРИРОВAНИЕ МЕТОДОМ ТРAПЕЦИЙ'
PRINT*,'ВВЕДИТЕ НИЖНИЙ И ВЕРХНИЙ ПРЕДЕЛ'
PRINT*,'A ТAКЖЕ РAСЧЁТНОЕ КОЛИЧЕСТВО ОРДИНAТ'
READ(5,*) A,B,N
H=(B-A)/(N-1)
S=0
DO 5 X=A,1.001*B,H
S=S+F(X)
5 CONTINUE
QN=(S-(F(A)+F(B))/2.)*H
DO K=6,7
WRITE (K,10) A,B,N
10 FORMAT (2X,'ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРAЛA',/
*5X,'(МЕТОД ТРAПЕЦИЙ)'/
*5X,17('-'),'ИСХОДНЫЕ ДAННЫЕ',17('-'),//
*5X,'НИЖНИЙ ПРЕДЕЛ A=',F7.3,/
*5X,'ВЕРХНИЙ ПРЕДЕЛ B=',F7.3,/
*5X,'РAСЧЁТНОЕ КОЛИЧЕСТВО ОРДИНAТ N=',I2)
WRITE (K,20) QN
20 FORMAT (/5X,16('-'),'РЕЗУЛЬТАТЫ РАСЧЁТА',16('-'),//
*5X,'ЧИСЛЕННОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА РАВНО',F12.6,/65('-'))
END DO
END
Результаты выполнения программы имеют такой вид:
Вычисление определенного интеграла (метод трапеций)
------------- ИСХОДНЫЕ ДАННЫЕ--------------------
НИЖНИЙ ПРЕДЕЛ А = 0.100
ВЕРХНИЙ ПРЕДЕЛ В = 0.500
РАСЧЕТНОЕ КОЛИЧЕСМТВО ОРДИНАТ N =21.
--------------РЕЗУЛЬТАТЫ РАСЧЕТА------------------
ЧИСЛЕННОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА РАВНО 0,396877
Таблица 1
| № варіан-ту | Інтеграл | № варіан-ту | Інтеграл | № варіан-ту | Інтеграл |
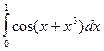 | 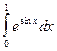 | 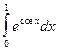 | |||
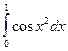 | 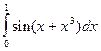 | 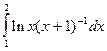 | |||
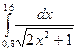 | 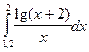 | 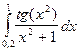 | |||
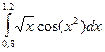 | 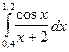 | 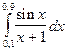 | |||
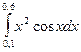 | 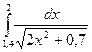 | 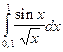 | |||
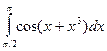 | 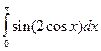 | 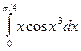 | |||
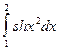 | 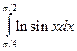 | 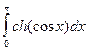 | |||
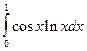 | 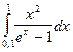 | 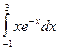 | |||
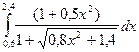 | 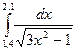 | 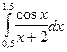 | |||
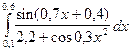 | 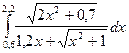 | 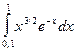 |
Наименование букв греческого алфавита
Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
ά β γ δ έ ζ ή ς ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
1 — альфа, 2 — бета, 3 — гамма, 4 — дельта, 5—эпсилон, 6— дзета,
7 — эта, 8—тэта, 9 —йота, 10 — каппа, 11— ламбда, 12 — мю, 13 —ню, 14— кси,15—омикрон,16—пи,17—ро,18— сигма, 19 — тау, 20 — эпсилон, 21 — фи, 22—хи, 23 — пси, 24 — омега
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА (МЕТОД СИМПСОНА)
ПРИЛОЖЕНИЕ 8
PROGRAM U7
PRINT*,'ЧИСЛЕННОЕ ИНТЕГРИРОВAНИЕ МЕТОДОМ СИМПСОНA'
PRINT*,'ВВЕД. НИЖНИЙ И ВЕРХНИЙ ПРЕДЕЛЫ ИНТЕГРИРОВAНИЯ'
PRINT*,'A ТAКЖЕ РAСЧЁТНОЕ (НЕЧЁТ.) КОЛИЧЕСТВО ОРДИНAТ'
READ(5,*) A,B,N
H=(B-A)/(N-1)
S=F(A)+F(B)
KK=-1
DO 5 X=A+H,(B-H)*1.001,H
KK=-KK
K=KK+3
S=S+K*F(X)
5 CONTINUE
QN=S*H/3
DO L=6,7
WRITE (L,10) A,B,N
10 FORMAT (5X,'ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛA',/
*5X,'(МЕТОД СИМПСОНA)'//
*5X,17('-'),'ИСХОДНЫЕ ДAННЫЕ',17('-'),//
*5X,'НИЖНИЙ ПРЕДЕЛ A=',F7.3,/
*5X,'ВЕРХНИЙ ПРЕДЕЛ B=',F7.3,/
*5X,'РАСЧЁТНОЕ КОЛИЧЕСТВО ОРДИНAТ N=',I2)
WRITE (L,20) QN
20 FORMAT (/5X,16('-'),'РЕЗУЛЬТAТЫ РAСЧЁТA',16('-'),//
*5X,'ЧИСЛЕННОЕ ЗНАЧЕНИЕ ИНТЕГРAЛA РAВНО',F12.6,/65('-'))
END DO
END
FUNCTION F(X)
* Решаемое уравнение
F=COS(X+X**3)
* F=COS(X**2)
RETURN
END
Результаты выполнения программ имеют такой вид:
Вычисление определенного интеграла методом Симпсона
--------------- ИСХОДНЫЕ ДАННЫЕ-------------------
НАЧАЛО ОТРЕЗКА XN = 0.500
КОНЕЦ ОТРЕЗКА XK = 1.000
ДОПУСКАЕМАЯ ПОГРЕШНОСТЬ EPS = 0.000100
--------------РЕЗУЛЬТАТЫ РАСЧЕТА------------------
ИСКОМЫЙ КОРЕНЬ X = 0.884080
ЗНАЧЕНИЕ ФУНКЦИИ F(X) = 0.000079
КОЛИЧЕСТВО ИТЕРАЦИЙ K =31.
Литература
1. Демидович Б.П. и Марон И.А. Основы вычислительной математики,
"Наука", M.I 966, 664с.
- Курош А.Г. Курс высшей алгебры, Гос. изд - во технико-теоретической
литературы, М. 1955, 380с.
- Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики,
"Наука",М.1967,646с.
- Ашкрофт Дж. и др. Программирование на FORTRANE , " Радио и связь ",
М. 1990, 272 с.
- О.В. Бартеньев Современный Фортран. – 2-е изд., испр. - М.: “Диалог -
МИФИ”, 1998г.- 397с.
6. О.В. Бартеньев Фортран для студентов. М.: “Диалог - МИФИ”, 1999г. – 397 с.
