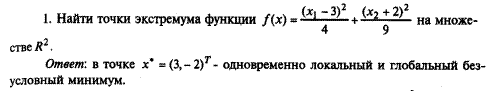Критерии проверки достаточных и необходимых условий второго порядка в задаче поиска безусловного экстремума

1.3. Задание. Определение экстремумов с использованием необходимых и достаточных условий
Найти экстремум функции 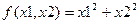 , используя необходимые и достаточные условия.
, используя необходимые и достаточные условия.
1. Открыть документ Градиент.
Переместить курсор в конец документа. Получить аналитический вид градиента функции при помощи символьной математики, введя операцию ® панели инструментов Symbolic
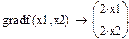
Очевидно, градиент обратится в 0 при x1=x2=0.
2. Проверим достаточные условия. Используем первый способ, заключающийся в определении знаков угловых миноров.
Определим знаки угловых миноров матрицы Гессе
2>0;
теперь вычислим определитель матрицы Гессе. Для этого введем шаблон определителя матрицы из панели Vector and Matrix
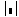
в него введем имя функции, определяющей матрицу Гессе и потребуем символьного вычисления, введя операцию ® панели инструментов Symbolic
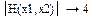
Второй минор также положителен. Значит найденная точка является точкой минимума функции.
3. Рассмотрим второй способ определения достаточности через собственные числа матрицы Гессе. Для этого введем шаблон функции eigenvals, где в качестве имени матрицы укажем имя функции, задающей матрицу Гессе и потребуем символьного вычисления значений
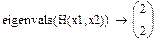
Поскольку все собственные числа матрицы Гессе положительны, точка экстремума функции является точкой минимума.
4. Сохранить файл.
5. Найти и классифицировать экстремумы функции 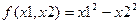 , определенную в файле Форма 1.
, определенную в файле Форма 1.
6. Результаты сохранить в файле Форма 1.
7. Найти и классифицировать экстремумы функции 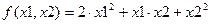 ,.
,.
8. Результаты сохранить в файле Форма 2.
1.4. Задание. Определение экстремумов графическим способом в MathCad
Найти экстремумы функции 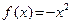 на множестве
на множестве 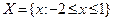 .
.
1. Создать новый документ.
2. Ввести шаблон двумерного графика X-Y. В шаблон аргумента оси абсцисс ввести имя 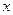 , в качестве аргумента оси ординат ввести функцию
, в качестве аргумента оси ординат ввести функцию 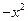
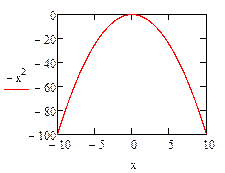
3. Отформатировать область определения 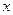 согласно заданию, используя шаблоны ввода пределов осей на графике
согласно заданию, используя шаблоны ввода пределов осей на графике
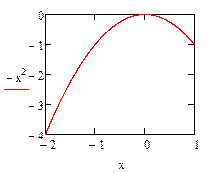
4. Определить точки локального и глобального минимумов функции.
5. Сохранить документ под именем График.
6. Аналогичным образом определить экстремумы функции 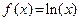 на множестве
на множестве 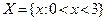 .
.
1.5. Задание. Определение экстремумов графическим способом
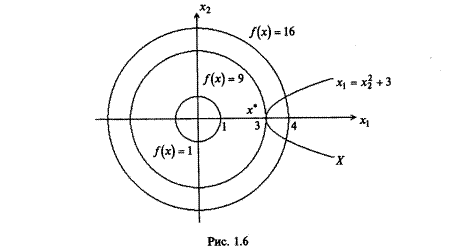
Найти экстремумы функции 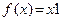 на множестве
на множестве 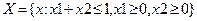 .
.
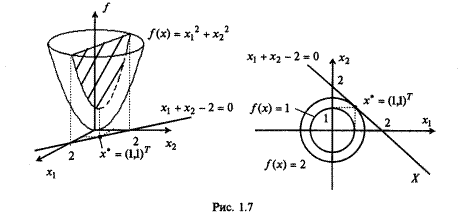
Решается задача поиска условного экстремума. Линии уровня имеют уравнение 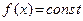 и являются прямыми, параллельными оси
и являются прямыми, параллельными оси 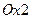 .
.
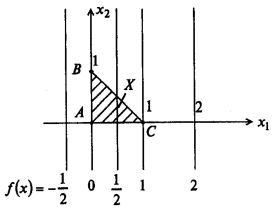
Множество допустимых решений, где выполнены все ограничения, заштриховано на рис. ниже.
В точке 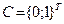 функция достигает глобального максимума.
функция достигает глобального максимума.
На множестве отрезка АВ достигается глобальный минимум со значением целевой функции 0
1.6. Задание. Графическое решение задач оптимизации