Данное тригонометрическое уравнение является однородным первой степени относительно sin x и cos x

Разделим обе части этого уравнения на cos x ¹ 0, получим:

tg x + 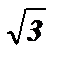= 0 ; tg x = ; x = arctg ( ) + pk ; x = + pk , k Î Z .

Ответ: x = + pk , k Î Z .

Пример №2: Решить уравнение: 5 sin ² x + 3 cos ² x = 4 sin 2x .

Решение:

Воспользуемся формулой sin 2x = 2 sin x cos x :

5 sin ² x + 3 cos ² x - 8 sin x cos x = 0 ;

Полученное тригонометрическое уравнение является однородным второй степени относительно sin x и cos x . Разделим обе части этого уравнения на cos ² x ¹ 0, получим: 5 tg ² x - 8 tg x + 3 = 0;

Введем новую переменную у = tg x , получим квадратное уравнение:

5 y ² - 8 y + 3 = 0; D = b ² - 4ac; D = (- 8 ) ² - 4 · 5 · 3 = 4;

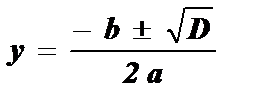; ; y₁ = ; y₂ = 1 ;

tg x = ; x = arctg + pk , k Î Z .

tg x = 1 ; x = arctg 1 + pk ; x = 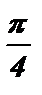+ pk , k Î Z .

Ответ: x = arctg + pk , x = 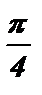+ pk , k Î Z .

Пример №3: Решить уравнение: 3 sin ² x - 4 sin x cos x + 5 sin ² .

Решение:

Воспользуемся формулой .

C помощью формулы sin ² x + cos ² x = 1 выполним замену

2 = 2 ·1 = 2 (sin ² x + cos ² x ) .

3 sin ² x - 4 sin x cos x + 5 (- cos x ) ² = 2 (sin ² x + cos ² x );

3 sin ² x - 4 sin x cos x + 5 cos ² x - 2 sin ² x - 2 cos ² x = 0;

sin ² x - 4 sin x cos x + 3 cos ² x = 0;

Полученное тригонометрическое уравнение является однородным второй степени относительно sin x и cos x .

Разделим обе части этого уравнения на cos ² x ¹ 0, получим:

tg ² x - 4 tg x + 3 = 0;

Введем новую переменную у = tg x , получим квадратное уравнение:

у ² - 4 у + 3 = 0; D = b ² - 4ac; D = (- 4) ² - 4 · 1 · 3 = 4;

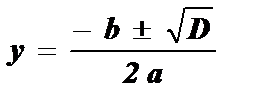; ; y₁ = 3 ; y₂ = 1 ;

tg x = 3 ; x = arctg 3 + pk , k Î Z .

tg x = 1 ; x = arctg 1 + pk ; x = 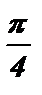+ pk , k Î Z .

Ответ: x = arctg 3 + pk , x = 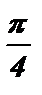+ pk , k Î Z .

Замечание: Если в уравнении a sin ² x + b sin x cos x + с cos ² x = 0 коэффициенты a = 0 или с = 0 , то уравнение решается разложением левой части на множители:

a = 0 Þ b sin x cos x + с cos ² x = 0 Û cos x ( b sin x + с cos x ) = 0

с = 0 Þ a sin ² x + b sin x cos x = 0 Û sin x ( a sin x + b cos x ) = 0 .

Пример №4: Решить уравнение: 2 sin x cos x - 2 cos ² x = 0 .

Решение:

Вынесем общий множитель cos x за скобки , получим :

2 cos x ( sin x - cos x ) = 0 ;

Разделим обе части уравнения на 2 :

cos x ( sin x - cos x ) = 0 ;

Произведение равно нулю , если хотя бы один из сомножителей равен нулю, а другой определен. Приравняем к нулю каждый сомножитель, получим:

cos x = 0; х =

sin x - cos x = 0 ;

Данное тригонометрическое уравнение является однородным первой степени относительно sin x и cos x . Разделим обе части этого уравнения на

cos x ¹ 0, получим:

tg x - 1 = 0 ; tg x = 1; x = arctg 1 + pk ; x = + pk , k Î Z .

Ответ: х = x = 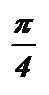+ pk , k Î Z .

Тригонометрические уравнения, решаемые с помощью разложения на множители. Другие тригонометрические уравнения.

Замечание: При решении тригонометрических уравнений, содержащих тангенсы и котангенсы, устанавливается область допустимых значений, чтобы исключить значения переменной, при которых эти функции не определены.

При решении тригонометрических уравнений, содержащих дроби, устанавливается область допустимых значений, так как необходимо исключить значения переменной, при которых знаменатели дробей обращаются в нуль.

Пример №1: Решить уравнение: sin x tg x + 1 = sin x + tg x .

Решение:

х

у

Определим область допустимых значений данного уравнения: tg x не существует при углах вертикального диаметра , значит х ¹ .

sin x tg x + 1 - sin x - tg x = 0;

Преобразуем левую часть в произведение с помощью группировки:

sin x tg x - sin x + 1 - tg x = 0;

sin x ( tg x - 1 ) - ( tg x - 1 ) = 0;

( tg x - 1 ) ( sin x - 1 ) = 0;