Этапы решения (отделение корней и методы уточнения корней)
Лабораторная работа 8. Объектно-ориентированный подход к описанию численных методов
Задание.Работа выполняется командой из 2-4 человек. Каждая команда занимается численными методами для решения определенного класса задач, разрабатывает недостающие методы, тестирует все родственные методы и делает вывод о качестве тех или иных методов. Для визуализации и сравнения результатов выводятся графики
Классы задач:
1. Решение нелинейных уравнений (4 чел.)
Отделение корней
Метод половинного деления;
Метод простых итераций ;9
Метод Ньютона(метод касательных) ;
Модифицированный метод Ньютона(метод секущих )
Метод хорд.
2. Интерполирование функций полиномами(2 чел.)
Полином Ньютона
Полином Лагранжа
3. Аппроксимация функций(3 чел.)
Сглаживание опытных данных методом наименьших квадратов
Решение системы линейных уравнений методом Гаусса
Решение системы линейных уравнений методом Крамера
Решение системы линейных уравнений методом простой итерации
Решение системы линейных уравнений методом Зейделя
Вычисление полинома по схеме Горнера
4. Вычисление определенного интеграла(3 чел.)
Метод прямоугольников
Метод трапеций
Метод Симпсона
5. Решение задачи Коши для дифференциального уравнения(2 чел.)
Метод Рунге - Кутта 1-го порядка (метод Эйлера) - есть
Метод Рунге - Кутта 4-го порядка - есть
Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера)
Решение нелинейного уравнения
Этапы решения (отделение корней и методы уточнения корней)
Необходимость отыскания корней нелинейных уравнений встречается при расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
Дано нелинейное уравнение: 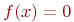 |
Необходимо решить это уравнение, то есть найти его корень 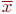 .
.
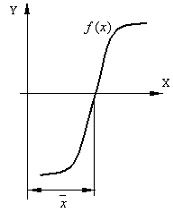
Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b], в котором лежит уточняемый корень уравнения (рис. ).
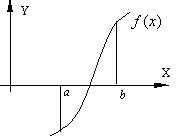
Рис.
Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется отделением этого корня.
Процесс отделения корней проводят, исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, то есть f(a)f(b)<0, то между точками a и b имеется хотя бы один корень уравнения. Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.
Процесс определения корней уравнений состоит из 2 этапов:
1. отделение корней, то есть определение интервалов изоляции [a,b], внутри которого лежит каждый корень уравнения;
2. уточнение корней, то есть сужение интервала [a,b] до величины равной заданной степени точности 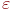 .
.
Для уравнений используются следующие методы уточнения приближенных значений действительных корней:
1. метод половинного деления;
2. метод простых итераций ;
3. метод Ньютона(метод касательных) ;
4. модифицированный метод Ньютона(метод секущих );
5. метод хорд.
